# ML / DL

### Gradient Descent，Stochastic Gradient Descent
- GD
- 样本很大时，计算消耗很大
- learning rate不好选择，lr太小 收敛慢，lr太大 算法不收敛
- SGD
- 每次只取一个样本
- 增加跳出local minimal的潜力
- Mini Batch SGD
- gradient比用一个样本计算出来的稳定

### **梯度消失vanishing、梯度爆炸exploding**：activation function的导数为0，w停止update或者update很慢。

- 原因
- NN角度：BP的链式法则导致的，一串链接下去，如果都大于1:爆炸，如果都小于1:消失。
- 激活函数角度：比如sogmoid在x<-5 和 x>5的区间，导数就非常接近0了。
- 解决方案
- 对梯度爆炸：剪切、正则
- 用relu：更新速率都是1.
- batchnorm:
- at each layer, normalize the output, and scale them to a good range using $\alpha, \beta$
- residual network: prevent **gradient vanishing**. So called “identity shortcut connection”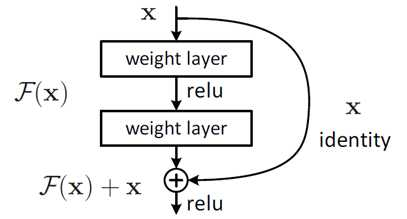 
- **Something about RELU:** 在x > 0的部分没有问题，导数始终是1；在x < 0 的部分，导数是0，neurons 就死了 停止更新。一种解决办法是leaky relu，在x < 0的部分加一个小小的斜率。
- 优点：计算快；因为梯度是1，解决了梯度爆炸的问题
- 缺点：负数部分全是0；输出不是0为中心。

### SVM
**Large margin classifier**
- SVM中的$C$，也是在控制regularization的多少

- SVM初衷：SVM要找一个“最适合”的超平面。最适合？有着最大间隔的超平面！

- SVM的目标函数
如果让第一项为0，也就是说所有的sample都分类正确，而且不能离margin太近。优化目标就变成了最小化 $\sum_{i=1}^{n} \theta_{j}^{2}$，（在全部能分对的情况下）。这个优化目标直接导致了large margin classifier

- 为什么上面的目标方程会导致large margin？
在左面（不好）的情况下，为了满足s.t.的条件，因为p比较小，就要$|\theta|$比较大，所以不能很好的满足优化目标。在右面的情况下，p比较大，比较小的$|\theta|$就能满足s.t.的条件，是更好的优化结果。
上面例子说明了，上述的优化条件会导致large margin。
- 一个data point到超平面的距离，就是函数距离$\frac{y\widehat{y}}{||w||}$，即函数距离除以||w||。函数距离不能做数，因为成倍的增加w和b，函数距离会增
加一倍。
- 我们把函数距离确定成1，这样对问题没有变化。至此，最大化margin的问题就转化成了最大化1 / ||w||，s.t. y (w^T x + b) > 1 的问题 。再转化成最小化 ||w||^2的问题。
- Use slack to handle outliers
- 有时候存在噪音，造成不能完美的分割
- 考虑到outliers的问题，引入松弛变量，其参数为C。C来控制目标函数中两项的权重（“寻找margin最大的超平面”和“保证数据点偏差量最小”）。即 加大松弛，就有更多的点能被分对，但是margin会减小；减小松弛，margin会变大，但是一些点就不在正确的阵营了。
- Lagrange multiplier，to optimize with constraint.
- SVM通过核函数kernel的运用，在高维空间中寻找超平面，解决在原始空间线性不可分的情况。
- 但是怎么处理把变量映射到了高维空间，再做内积时候指数爆炸的结果呢？
- 碰巧的是，SVM中需要计算的数据向量也是总以内积形式出现的。所以可以直接在低维空间中计算，不需要显式的写出映射后的结果。
- 常用的核函数
- 多项式核
- 高斯核。
- 将原始空间映射到无穷维；高次特征的权重衰减的非常快，所以相当于一个低维的子空间。
- 高斯核具有很高的灵活性
- tanh
- SVM的另一种理解：hinge loss + L2 regularization。前一项和slack有关，后一项和最大化margin有关
- Logistic Regression 和 SVM的异同
- 同：
- 通常都处理二分类问题
- 异：
- 目标函数不一样：logistic loss 和 hinge loss
- SVM的处理方法是只考虑support vectors，也就是和分类最相关的少数点；Logistic Regression通过非线性映射（sigmoid），大大减小了离超平面较远的点的权重（函数值非常接近1和0），提升了与分类最相关的数据点的权重。

### Kernels
kernel：**去描述两个输入之间的similarity。Is the inner product of some functions (mapping data to higher dimentions)**

**We constrained optimization problem can be written as a Lagrangian dual problem, which contains the inner product of all the feature pairs**

Instead of compute the higher dimentional feature explicitely, we compute using the kernel function.

- 之前用过high level polynomials，但是太贵了。
- Kernel
上面是一个kernel的例子，把x转换为到三个landmark的similarity。Each landmark can create a new feature.
假设用新造出的feature，给定$|\theta|$的取值。那么预测+1的decision boundary就是包围l1 l2的部分。
怎么选择landmark的位置呢？就在每个sample上放一个。这样每个x就有了N个similarity（feature）。
- SVM with kernels
在目标方程的前一项，以前算得是$|\theta^Tx|$，现在是$|\theta^Tf|$。
值得一提的是，最后一项通常会写做$\theta^TM\theta$，是为了优化更快。
- SVM parameters
- C
- large C：lower bias，high variance
- small C：higher bias， lower variance
- $\sigma$ in kernels
- large $\sigma$: feature varies more smoothly, higher bias, lower variance.
- small $\sigma$: feature varies less smoothly, lower bias, higher variance.

- SVM in practice
- Need to specify C and kernel
- linear kernel: feature多，sample少。sample少，不用kernel，防止overfit。
- Gaussian kernel，need to choose $\sigma$。feature少，sample多. It's important to perform feature scaling before using kernels. 因为kernel中要计算两个feature之间的差。

- SVM VS. Logistic regression
- Many features, small data samples: linear classifier
- Less featurs, intermediate data samples: SVM with Gaussian kernel
- Less features, large data samples: create more features, use linear classifier.

### Prior of L1 or L2 regularization
- 之前我们一直在maximize likelihood $P(y|\theta)$, 而Bayes theorem中，我们最大化posterior 
- 在最大化posterior的过程中，相比之前的likelihood，多出了prior产生的一项。
- If we choose **Gaussian** prior, it leads to a L2 norm. $\lambda\propto\frac{1}{\sigma^2}$. 非常符合直觉，Gaussian prior的方差越小，parameters越有可能接近0，相当于regularization越大。
- If we choose **Laplacian** prior, it leads to a L1 norm.. $\lambda\propto\frac{1}{b}$
- Difference of L1 and L2 regularization
- L2：
- L2 prevents one of the parameter to be too large.
- overfit的时候，拟合函数需要去顾虑每一个点，最终的拟合函数波动很大，某些w值很大。
- 先验分布是高斯分布，趋向0周围
- 当我们有许多不太有用的features时，比较有用。
- L1：
- L1 leads to sparsity
- 逼迫更多w为零。能够实现特征的自动选择。
- 先验分布是拉普拉斯分布，在0附近上升的更陡峭，趋向于0本身。

### Logistic Regression 和 Linear Regression
- 前者对输出施加了一个sigmoid函数，将输出压缩到了0-1，实现二分类。其目标函数也因此从差平方和函数变为对数损失函数。
- Sigmoid函数是Softmax的二元特例。多分类问题，就要用Softmax了。

### Bias-Variance tradeoff
- a **set of predictive models** whereby models with a lower bias in parameter estimation have a higher variance of the parameter estimates across samples, and vice versa.
- The **bias** error is an error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting).
- The **variance** is an error from sensitivity to small fluctuations in the training set. High variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs (overfitting).

- Bias: underfit; training error和validation error都大。增加traing smaples 没什么用，因为模型本身不够复杂。两种error都在比较高的水平。

- Variance: overfit；training error小，validation error大。增加traing samples可以减少这种gap。traning error在比较低的水平。

irreduceble error + learning error

complexity 上升，bias下降，variance上升
反之也成立

### Batch Normalization
- Intuition:
- Similar to linear regression, we normalize activations of each layer, to make training more efficiently.
- Why?
- The big change of input wont influnce deeper layers much, make training more stable, may speed up training.
- Slightly regularization. In training process, $\mu$ and $\sigma$ are calculated only using the a mini-batch, add noise. Just like dropout
- Notice:
- Traing:
- just use one mini-batch to calculate $\mu$ and $\sigma$.
- Keep track of a running average of $\mu$ and $\sigma$ (for test time)
- Idealy, calculate $\mu$ and $\sigma$ using the final network with full training set.
- Update scale factors $\alpha,\beta$.
- Testing:
- Using the running $\mu$ and $\sigma$ from training
- In practise, often using in $z$ (before activation)
- $\alpha,\beta$ use to adjust activation function so as to better use non-linearty.

### 解决overfit的办法：
- 正则化
- L2：
- overfit的时候，拟合函数需要去顾虑每一个点，最终的拟合函数波动很大，某些w值很大。
- 先验分布是高斯分布，趋向0周围
- 当我们有许多不太有用的features时，比较有用。
- L1：
- 逼迫更多w为零。能够实现特征的自动选择。
- 先验分布是拉普拉斯分布，在0附近上升的更陡峭，趋向于0本身。
- Dropout：
- 在训练的运行的时候，让神经元以超参数p的概率被激活(也就是1-p的概率被设置为0), 每个w因此随机参与, 使得任意w都不是不可或缺的, 效果类似于数量巨大的模型集成。
- Early Stoping
- Reduce features
- 手动或自动选择一些features
- BatchNormalization
- 网络bagging
### 归一化 Normalization
- 1）归一化后加快了梯度下降求最优解的速度（椭圆变圆）
- 2）归一化有可能提高精度（KNN中量刚不同，造成误差）
- 通过梯度下降法求解的模型一般都是需要归一化的，比如线性回归、logistic回归、KNN、SVM、神经网络等模型。
- 但树形模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、随机森林(Random Forest)。
- 特征选择：
- 好处：
- 降维，增加generializ的能力，减小overfit的风险
- 方法：
- 去除方差较小的特征
- regularization
- SVD？

### Generative Models
- **Generative approach**, in which it is assumed that the underlying distribution over the data has a specific parametric form and our goal is to estimate the parameters of the model. This task is called parametric density estimation.
- **Discriminative** approach in which our goal is not to learn the underlying distribution but rather to learn an accurate predictor.
- 一种可以估计distribution参数的统计学方法，叫做**maximum likelihood principle**
- 首先假设一个分布，e.g. Gaussian
- 让所有observation在Gaussian中有最大的Likelihood，$\prod_i{P(x_i|\theta)}$
- 对$P$求$\theta$的导数。（对于Gaussian的例子，计算出来的$\mu$和$\sigma$正是所有observation的均值和方差）。
- MLE和loss的关系
- 最大化MLE的过程等价于最小化$-log(P(X|\theta))$，也叫log loss
- 这个loss的期望是。第一项是relative entropy，在衡量我们估计的参数分布和原本的分布的距离。如果我们假设错了distribution的类型，即使是最好的参数，也会导致不好的模型（因为$P$ $P_\theta$ 不一样）。
#### Naive Bayes
- Recall the Bayes optimal classifier 
- 假设我们现在的问题是：
如果要得到Bayes optimal classifier，需要$2^d$个参数。因为$x$有$2^n$种组合，每个组合对应一个$y$,.
- **Naive Bayes**假设，每个feature之间是独立的：。这样Bayes optimal classifier就简化成了这样其中只有$2d+1$个参数了：在每个维度，有两个参数$p(x_i|y=0),p(x_i|y=1)$，再加一个参数$p(Y=y)$

#### Mixture of Gaussian
- Is a **parametric generative model**，$x$ is our observation, and $y$ is our latent variable (similar to cluster, but we don't know).
- The parameter $\theta=(c,(\mu1,...,\mu_k),(\sigma_1,...,\sigma_k))$ is a triplet, where $c_y=P_{\theta}[Y=y]$
- We use EM to optimize it.
- E step: we determine the probability that each example belongs to each cluster (assignment)
- We compute  using t step parameters
- M step: we update the centers on the basis of a weighted sum over the entire sample
- We compute  and 
- Some intuition:
- 在E step 中，我们想把一个sample分配到每个distribution中，很自然，就是要计算$w_i^{(k)}=p(y=k|x_i)$，展开成两项，变成$p(y=k)p(x_i|y=k)$，第一项是$c_k$(每个distribution的重要程度)，第二项就是第k个Gaussian的概率密度了。注意有归一化系数，s.t.每个sample分配到所有distribution的和为1，$Z_i=\Sigma_kw_i^{(k)}$.
- 在M step中，我们去计算每个分布的重要程度$c_k$和参数$\mu_k$
- $\mu_k$是所有$x_i$的加权（$w_i^{(k)}$）平均: $\mu_k=\frac{w_i^{(k)}x_i}{Z_k}$，$Z_k$是一个归一化系数，s.t.所有sample在这个cluster中的$w_i^{(k)}$和为1，$Z_k=\Sigma_iw_i^{(k)}$.
- $c_k$是说，每个cluster有多重要，$c_k$正比于所有sample属于k的权重之和$\Sigma_iw_i^{(k)}$，$c_k=\frac{\Sigma_iw_i^{(k)}}{Z}$. 有个归一化系数，s.t.所有的$c_k$家和为1，$Z=\Sigma_k\Sigma_iw_i^{(k)}$.

### K-Means
- 怎么找最佳的K？
- 观察法
- elbow method。看sum of distance随着K增大的变化，找到elbow的部分。
- K-means++，选取最优的初始点，初始点之间的距离要尽可能远
- step 1，随机抽出一个点
- step 2 计算其余点到这个点的距离，按照距离越大，可能性越高的原则，随机抽出第二个点
- step3 重复step2，直到抽出k个点
- 以这k个点作为初始的聚类中心，开始kmeans
### Bagging
- 学习器间不存在强依赖关系, 学习器可并行训练生成, 集成方式一般为投票
- 比如Random Forest
### AdaBoost
- 思想：从训练数据中学习一系列弱分类器或基本分类器，然后将这些弱分类器组合成一个强分类器。
- step1 初始化每个数据点的权值分布，一开始都是 1 / N
- step2 多轮迭代, m = 1, 2, 3, ..., M 轮
- a 用带有权值的数据点来训练这一轮的classifier G_m
- b 计算G_m的误差e_m
- c 计算G_m的系数，误差越高，G_m系数越小，在最终的组合classifier中作用越小 可以看到，如果错误率>0.5,系数变成负的，也能实际起到好的效果。
- d 更新没数据点的权重，被判断错的权重上升，判断对的权值下降。，上升或下降取决去exp中是+(错)/-（对），上升或下降的多少取决于当前classifier的performance（amount of say）

- step 3 按权重组合训练出的M个classifier G_m
- 常用decision tree来作为基本的classifier，因为是很好的weak learners
- 和random forest的区别：random forest中每个tree
- 都是等权重的
- 不是shallow的，而是完整长度的tree
- 每个都是independent的
### EM
### KNN
- K的选择，k太小 误差增大；k太大 过拟合
- 常见的Loss Functions：
- 用一个函数来估量模型的预测结果和真实结果的不一致程度。
- 0/1 loss
- log loss

### ROC曲线和曲线下的面积AUC：
- ROC曲线的来历：logistic regression原本的threshold是0.5，即0.5以下是负类，0.5以上是正类。但也可以调整整个threshold。在调整过程中，我们计算false positive rate作为x轴（预测为正，实际为负的样本占总样本的比例，这个比例越小越好）；true positive rate（预测为正，实际也为正的样本占所有样本的比例，这个比例越大越好）。
- 理解：threshold提高，true positive rate会减小，因为classifier只把非常有把握的归类为正，挑出来的+1肯定会变少；同时false positive rate减小，因为要求提高了，错把-1判断成+1的机会也小了。
- AUC是ROC曲线包围的面积，越大越好。
- AUC的另一种理解是：从所有1中抽取一个样本，从所有0中抽取一个样本，用训练好的classifier对他们排序，AUC就是把第一个样本排在第二个样本前的概率。所以AUC的取值0-1，1代表这个是完美的classifier，0.5代表这个classifier就是翻硬币，正常应在0.5-1之间。
### CNN
- CNN的卷积核
- 举例：filter的size实际3*3，那就是原图的9个点和filter上的9个点，对应位置相乘再相加。
- CNN能处理的问题：都存在局部与整体的关系，由低层次的特征经过组合，组成高层次的特征，并且得到不同特征之间的空间相关性
- CNN抓住此共性的手段主要有四个：局部连接／权值共享／池化操作／多层次结构。
- 局部连接使网络可以提取数据的局部特征
- 权值共享大大降低了网络的训练难度，一个Filter只提取一个特征，在整个图片（或者语音／文本） 中进行卷积
- 池化操作与多层次结构一起，实现了数据的降维，将低层次的局部特征组合成为较高层次的特征，从而对整个图片进行表示
- CNN pooling layer
- max pooling 相当于保留了这个2*2小方框内的最佳匹配结果，意味着cnn不在意特征在哪里匹配了，而在意是不是某个地方匹配成功了。
- 通过加入池化层，可以很大程度上减少计算量，降低机器负载。
- CNN通过pooling和stride可以达到降维的目的。
### Deep learning 调参经验：
- 参数初始化
- w初始化：高斯分布初始化
- 数据预处理：
- zero center，全部都减去均值
- 训练技巧：
- 要做梯度归一化,即算出来的梯度除以minibatch size
- dropout对小数据防止过拟合有很好的效果
- learning rate，从1或者0.1开始尝试，再validation set上检查，如果cost不下降了，就再折半。
- Ensemble
- 同样的参数,不同的初始化方式
- 不同的参数,通过cross-validation,选取最好的几组
- 同样的参数,模型训练的不同阶段，即不同迭代次数的模型
- 不同的模型,进行线性融合. 例如RNN和传统模型.
- DNN调参经验
- 合适的loss function
- square loss / cross entropy
- 合适的mini batch size
- 太大会陷入local minimum；太小会抖动太厉害
- batch size 会带来训练时间和训练准确率的tradeoff
- 合适的activation function
- sigmoid / relu
- 合适的自适应学习率（adptive learning rate）
- 使用动量 momentum
- 有助于冲出local minimum
- t这个点变化的方向：V_t = beta * V_(t-1) + alpha * del_w(L); 当前weights的变化：W = W - V_t
- Activation Functions
- sigmoid：
- g(z) = 1 / (1 + exp(-z)), z 是一个线性组合
- 有梯度消失的问题
- 计算慢
- 关于原点不对称
- Tanh
- 有梯度消失的问题
- 比sigmoid稍快
- Relu
- 收敛速度很快
- 正向没有梯度消失，负向神经死亡且不会复活
- Leaky ReLu
- Maxout
- ReLu为什么比Sigmoid Tanh更优秀一些？
- 计算量小，不论正向还是反向
- sigmoid反向传播很容易导数接近0
- ReLu会使一部分神经元输出为0，这样就造成了网络的稀疏性，减小了参数的依存关系，缓解过拟合。
- 梯度爆炸怎么办
- 减小网络尺寸
- 使用relu
### 目标检测 Object Detection
- 传统object detection
- region proposal（穷举策略，用sliding window，且改变尺寸；时间复杂度高）
- 特征提取（HOG）
- classifier（SVM、Adaboost）
- Object Detection的检测评价函数：intersection-over-union，最理想情况 IOU == 1
- RCNN family
- RCNN，一张图（47s左右）
- 图片input
- selective search （～2000RoI）
- 根据颜色、边缘、纹理等等快速的查找到可能存在的region proposal
- resize（resize过的图片不好求导）
- Conv （等于做2000次Conv），将CNN的fully connected layer输出作为特征
- 将每个region proposal提取到的CNN特征输出到SVM分类
- 具体训练步骤：
- Step1 训练（或下载一个）pre-trained model。比如一个训练好的能分1000类的CNN
- Step2 对该模型做fine-tuning
- 将分类数从1000给成21，20个object + 1个背景
- 去掉最后一个全连接层
- Step3 特征提取
- （用selective search）提取图像的region proposal
- 对每个区域，resize，用CNN做一次前向运算
- Step4 训练21个SVM（二分类）来判断候选框里的是不是这个目标
- Step5 使用regressor精准修正bounding box的位置
- Fast RCNN
- 图片input
- Conv
- selective search （避免选到重叠的部分）（bottle neck）
- RoI Pooling （避免resize，而让输出结果有一样的size）：一个RoI选取其中最大的值 max pooling，也可以2*2选4个，或3*3选9个
- dense
- softmax多分类/bbox reg做回归
- Faster RCNN
- Conv Layers: VGG16 为例，13个Conv层（kernelsize=3，pad=1，stride=1），13个relu层，4个pooling层
- RPN 生成可能的框
- 将特征图中的每一个点看作是一个组合长方形的中心点（anchor）
- 这些长方形有三种长度/三种比例，共九个长方形
- 在feature map上：一系列点 --> 一系列框
- 用交并比判断是物体(>0.9)还是背景(<0.2)，中间部分舍去。
- 回归梯度
- 对框的中心点平移
- 比例缩放
- 分类层：softmax：2k scores（是/不是目标）
- 边框回归层：reg layer：4k coordiantes。对每个边框转换，有两个平移参数，两个缩放参数需要学习
- Region proposal + feature map -- > RoI Pooling（避免resize，而让输出结果有一样的size）：一个RoI选取其中最大的值 max pooling，也可以2*2选4个，或3*3选9个
- RoI pooling --> classifier
- softmax多分类/bbox reg做回归
- YOLO（you only look once）
- YOLO将目标检测任务转换成一个回归问题，大大加快了检测的速度，使得YOLO可以每秒处理45张图像。而且由于每个网络预测目标窗口时使用的是全图信息，使得false positive比例大幅降低（充分的上下文信息）。
- 但是YOLO也存在问题：没有了Region Proposal机制，只使用7*7的网格回归会使得目标不能非常精准的定位，这也导致了YOLO的检测精度并不是很高。
### Vehicle Detection Model
- Features：
- color histogram
- different color space
- HOG features
- Sliding window + SVM
### Dlib
- HOG features （HIstogram of Oriented Gradient）
- HOG 常和SVM结合使用
- HOG 算法。将图像分成若干个cell，如8*8=64个像素为一个cell。在每个cell内统计梯度直方图（如将所有梯度方向分为9个bin）。2*2的cell组成一个block，所以每个block中有9*4个特征。一个block作为一个整体归一化。
- 颜色空间归一化
- 梯度计算
- 梯度方向直方图
- 重叠块直方图归一化
- HOG特征
### LeNet
- CSCSCFO
- C：convolution layer；S：subsampling；F：fully connected；O：output
- convolution之后用relu激活
- cross_entropy：
- the distance between score and the ground truth。
- cross_entropy = -Sigma(y_truth*log(y_hat))。 y_truth取值是0/1 after one hot encode; y_hat是1*n的向量，n是features的数量，每个数字代表这个sample是这个类的可能性。
- 分类training 过程中用它作为loss funciton。但是test中，还是可以用准确率，更加直观
- Transfer learning (VGG16)
- VGG16: 反复堆叠3*3的Conv和maxpooling。结构简单，但参数多训练量大
- ccp ccp ccp cccp cccp fff
- Transfer learning：
- 决定如何使用迁移学习的因素有很多，这是最重要的只有两个：新数据集的大小、以及新数据和原数据集的相似程度。有一点一定记住：网络前几层学到的是通用特征，后面几层学到的是与类别相关的特征。
- 新数据集比较小且和原数据集相似。因为新数据集比较小，如果fine-tune可能会过拟合；又因为新旧数据集类似，我们期望他们高层特征类似，可以使用预训练网络当做特征提取器，用提取的特征训练线性分类器。
- 新数据集大且和原数据集相似。因为新数据集足够大，可以fine-tune整个网络。
- 新数据集小且和原数据集不相似。新数据集小，最好不要fine-tune，和原数据集不类似，最好也不使用高层特征。这时可是使用前面层的特征来训练SVM分类器。
- 新数据集大且和原数据集不相似。因为新数据集足够大，可以重新训练。但是实践中fine-tune预训练模型还是有益的。新数据集足够大，可以fine-tine整个网络。
- Image Augmentation
- rotation, shift, sheer, flip
- Cross Entropy：
- the distance between score and the ground truth。作为多分类的一种loss function。
- cross_entropy = -Sigma(y_truth*log(y_hat))。 y_truth取值是0/1 after one hot encode; y_hat是1*n的向量，n是features的数量，每个数字代表这个sample是这个类的可能性。
- 分类training 过程中用它作为loss funciton。但是test中，还是可以用准确率，更加直观
- Pooling: conv 的结果产生联系，取最大更加robust，防止overfit。
- mean pooling 求导：l+1层的结果，除以4，返回给l层的2*2的四个pixels。
- max pooling 求导：l+1层的结果，返回给l层中2*2中最大点的pixel，其他三个pixel为0。
- Sequence Neural Network
- named entitiy recognision(人命，公司名etc)
- 常见的字典3万-5万
- A generative algorithm models how the data was generated in order to categorize a signal. It asks the question: based on my generation assumptions, which category is most likely to generate this signal?
- A discriminative algorithm does not care about how the data was generated, it simply categorizes a given signal.
- Boosting
- 为了classifier不是deterministic：训练不同算法的classifier 或者 用不同的数据来训练。
- different algorithm：不同classifier的inductive 很类似，所以很可能犯同样的错误。这种ensemble会减小varience --> 会对training set的微小变化很敏感。
- different training data：Bagging
- 从N个sample中，生成M个training set（各自包含N个sample，抽取过程可重复）。
- 从N个sample中抽取N次的过程中，一个sample某次没被抽到的概率（1-1/N），N次都没抽到这个sample的概率（1-1/N）**N，取极限为0.3679
- Bagging可以减小varience，有regularization的作用。M个classifier每个都可能overfit，但会overfit到不同的地方，投票会抵消各种overfit。
- Boosting：weak learners -- > Strong learner
- AdaBoost (Adaptive boosting):
- runs in polynomial time and not much hyperparameters

### The regression problem
- Training date $\{(x_i,y_i)\}_{i=1}^{n}$--> Transformed data
- Taylor series
- $$\hat{f}(x)=\sum_{x=0}^{k-1}{f^{k}(0)\frac{1}{k!}x^k}$$

### 题号

- [20, 21, 23, 24, 25, 26, 27, 28, 29, 30, 35, 36, 37, 38, 39, 40, 43, 44, 45, 46,48, 49, 50, 51, 55,58, 66, 68, 69, 70, 73, 77, 80, 82, 86, 87, 88, 89, 91, 99, 100, 104, 108, 109, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137]
- 没理解：[52, 57， 55，59，60，61， 14， 6， 7， 16，19，70, 73]61很神 76特征选择 84 85 103 bias variance
- 应用题：95，98，101，102，105

### TODO list
- [ ] 用对不平衡数据集不敏感的算法：Tree，它使用基于类变量的划分规则去创建分类树，因此可以强制地将不同类别的样本分开。
- [ ] SVM
- [ ] batchnorm

### 衡量分类器的好坏
- TP/FN/FP/TN，前面的True False代表分类器分的对不对，后面的nagative positive代表分类器的结果是什么
- precision：TP/（TP + FP），在分类器认为是1的data points中，有多少真的是1
- recall：TP/（TP + FN），在所有的真正是1的data points中，分类器找出了多少
- F1 score：2 / F1 = 1 / recall + 1 / precision

### 数据不平衡？imbalancd dataset
- 采样：对小样本加噪声采样，对大样本进行下采样
- 数据生成：对已知样本生成新的样本
- 用对不平衡数据集不敏感的算法：Tree，它使用基于类变量的划分规则去创建分类树，因此可以强制地将不同类别的样本分开。
- 对loss function加权重。数据量少的类别loss算作更大。
- ~~进行特殊的加权：如在Adaboost中或者SVM中。~~
- ~~改变评价标准：AUC/ROC~~

### 怎么处理缺失值，missing data？

- 如果缺失的太多，直接丢弃这个特征
- 用均值/众数 填充，连续型用中位数补
- 用随机森林等算法预测填充？
### 线性分类器和非线性分类器：

- 线性：logistic regression，naive bayes，perceptron，
- 非线性：decision tree，random forest，neural network
- SVM看用什么核函数，linear / Gaussian
- 熵（entropy）：定义为离散随机事件出现的概率：系统越有序，信息熵越低；系统越无序，信息熵越高。
- 牛顿法：
- 牛顿法是一种近似求解方程的方法。
- 从初始点x0开始，做函数的切线，切线和x轴相交于x1 （x1肯定比x0更接近方程的解）
- 做(x1, y1)的切线，切线和x轴相交于x2（x2肯定比x1更接近方程的解）
- ...
- 牛顿法和梯度下降法：
- 牛顿法收敛速度更快，但是要计算hessian矩阵的逆矩阵，计算更费时。

### SVD
$Rank(AB)<=min(Rank(A), Rank(B))$, 因为$U,V$都是independent的，所以$Rank(A)=Rand(\Sigma)$
如果多拿掉一个$\Sigma$中一个非0的维度，还原回$A'$，那么$A'$是所有rank是k-1的matrix中，最接近$A$的。

### Graph Cut

### Logistic Regression
- 用logistic函数（sigmoid）将x映射带（0-1）上，映射后的值是y=1的概率。大于0.5属于1类，小于0.5属于-1类。$H_{\mathrm{sig}}=\phi_{\mathrm{sig}} \circ L_{d}=\left\{\mathbf{x} \mapsto \phi_{\mathrm{sig}}(\langle\mathbf{w}, \mathbf{x}\rangle): \mathbf{w} \in \mathbb{R}^{d}\right\}$
- 为什么用sigmoid，而不用least square fit？
- 如果用linear regression：**outlier会有很大影响**，很远离decision boundary的sample，本来可以很容易的被判断为是一类，但是还是会对decision boundary造成很大影响（bad）
- 用sigmoid function可以解决上述问题。这里涉及到一个小问题，对于$H_{sig}$，threshold是0.5，对于$\langle\mathbf{w}, \mathbf{x}\rangle$，threshold是0.所以是linear classifier。
- 一个拓展，如果把$\langle\mathbf{w}, \mathbf{x}\rangle$的部分，换成是一个对于$\mathbf{x}$的non-linear映射，也就构成了一个新的non-linear classifier。
- 怎么设计loss function呢？
- $cost(h_w(x),y)=（h_w(x)-y）^2$，是非convex的！因为二次函数叠加了$h()$
- 所以定义另一种loss function，log loss
- if $y=1, cost=-\log{(h(x))}$, $h\in[0,1]$
- if $y=0, cost=-\log{(1-h(x))}$
- 结合起来：$cost=-y\log(h(x))-(1-y)\log(1-h(x))$
- 上式可以用MLE推导出来
- 怎么估计loss function中的参数？
- 用gradient descent
- logistic regression 和 linear regression 更新的形式是一样的，只是$h(x)$不同，分别是上图的红色和蓝色。
- coding时候只用code gradient，cost没用，只是用来monitor结果。
- Binary classification 推广到 multi-class classification
- one vs all
- Logistic Regression另一种理解：假设样本服从伯努利分布，求满足该分布的似然函数，对似然函数的对数求极值

### Machine learning applied suggestions
- 在测试集中表现较差：应该根据模型在训练集和验证集中的表现，判读模型是overfit还是under fit，采取对应的措施。
- Get more training samples
- Try smaller sets of features
- Try getting additional features
- ...
### ML system design
- Start with a simple algorithm
- Plot learning curves, decide if need more data, more features...
- Error analysis: 看判断错的样本有什么规律。要不要加新的features...
- 需要一个metric来衡量model。

### MLE is LS in linear model
b 来处理offset，
平移之前之后的$\hat{w}$是一样的