---
tags: summer_training
---
# Numeric System
## After the course you should learn
### Concept
1. Difference among `int, char, int8_t, uint32_t, float and double`.
2. Overflow detection and prevention
3. The limitation and usage of FP's different precision
4. The error cause by Floating Point
### Preface
The core of whole numeric system is to make a bunch of binary bits meaningful. CPU instruction interprets them in different ways depending on their types. In other words, you guys should be familiar with functions that have memory bits as input and mathematical meaning as output.
```=
B2U_w( w bit memory object ) => unsigned value (10)
B2T_w( w bit memory object ) => complement of unsigned value
```
Since the numeric system is all about function, [Range](https://en.wikipedia.org/wiki/Range_of_a_function) and [Domain](https://en.wikipedia.org/wiki/Domain_of_a_function) are critical in following discussion. Things always go wrong when **one-to-many** occurs.
## Integer Representation
### unsigned integer
A unsigned integer with w bits is able to represent value from 0 ~ $(2^w-1)$.
| binary | value |
|--------|-------|
| 0b000 | 0 |
| 0b001 | 1 |
| 0b010 | 2 |
| ..... | ~ |
| 0b111 | 7 |
What happens when we still add 1 on `0b111`? Since there are only **three** bits, `0b1000` is truncated into last three bits `0b000`. Here comes the issue. It is intolerable to have same memory bits affine to multiple value in domain set. **Overflow** happens!

### signed integer
Considering all existing integer, there are only three possibilities.
1. positive
2. negative
3. zero
In order to simulate real operation in mathematical world, it is necessary to make blob (binary large object) able to represent negative value and zero. To achieve our goal, we divide combinations into positive, negative value and zero.
#### One's complement
The most intuitive solution is to define the first bit as **sign bit**. With the sign bit, the only thing we have to do is to copy unsigned integer mechanism to signed integer just as following.

Yet, things become slightly weird but acceptable when we consider **zero**. In this system there would be two blob representing zero (many-to-one). Thus, one's complement wastes a combination. Previously, many CPU instruction support one's complement and use **negative zero** as a error sign representing error happens some where.

#### Complementary (Two's complement)
We try to define a pattern of memory bits that shares the same behavior in mathematical world (perfect world). The behavior includes following.
1. `0 == get_complement(0)`
2. `v + get_complement(v) == 0`
Considering these two criteria, one's complement fails. Thus, it is necessary to have other mechanism to represent value. Two's complement defines complementary operation as
```c=
negative_value = ~value + 1;
```
With two's complement, w bit of memroy blob is able to represent from $2^{w}-1$ to $-2^w$. One thing is worthy to mention is that (-1) in signed int means the largest value in unsigned system.
| binary | value | binary | value |
|--------|-------|--------|-------|
| 0b000 | 0 | 0b111 | -1 |
| 0b001 | 1 | 0b110 | -2 |
| 0b010 | 2 | 0b101 | -3 |
| 0b011 | 3 | 0b100 | -4 |
#### homework
```c=
// What is the result of printf?
#include <stdio.h>
#include <stdint.h>
void add_operands() {
uint32_t u = -1;
int32_t i = -1;
printf("result are %u and %d\n", u+i, u+i);
}
```
## Integer Operation
### Simple arithmetic
Things get a little bit complicated when operator get involved especially when two operands have different types. According to [C standard](https://wiki.sei.cmu.edu/confluence/display/c/INT02-C.+Understand+integer+conversion+rules), signed integer is converted to unsigned integer when two operands have different types.
```c=
uint32_t u = 10;
int32_t i = -5;
printf("u > i is %s\n", u > i? "true": "false"); // false
// 0x0000 000A > 0xFFFF FFFB
```
### Homework
Implement a function to detect whether the sum of two integers will overflow.
```c
#include <stdbool.h>
#include <stdint.h>
bool is_overflow(int32_t a, int32_t b) {
// ....
}
```
## Floating Point
### Representation
* [IEEE 754](https://zh.wikipedia.org/wiki/IEEE_754)
* Recall the logarithm calculation in high school
* characteristic 首數
* mantissa 尾數
* The only difference is **base = 2**
* A floating point is composed of three parts.
* sign bit
* exponential (exp)
* fraction (frac)
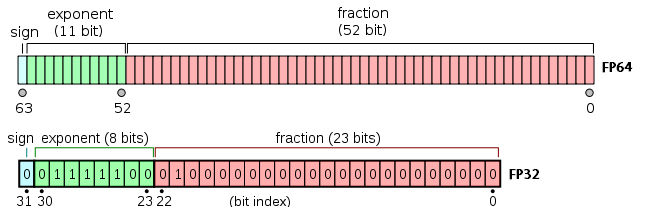
### Three formats
* The main difference is in **exponent**.

#### Special format
* If exponent is all **1**, the FP is either infinity or NaN (Not a Number).
* For infinity, fraction part is all **0**
* sing bit = 0 $(\ \infty)$
* sing bit = 1 $(-\infty)$
* Generally speaking, positive and negative infinity mean overflow. The result of two large numbers addition and multiplication.
* NaN often represents value undefined in real world. Ex: $\sqrt{-1}$ and $\infty-\infty$
#### Normalized format
* **Exponent** is either **not all 1** or **not all 0**.
* Normalized format focuses on representing value greater than 1 or less than -1.
<a id="Normalized_range"></a>

* In order to represent negative and positive value in **exponent** part, IEEE 754 defines a **bias** depending on its width. For a exponent with k digits, the bias value is $2^{k-1} - 1$. The resulting exponent $E = e - Bias$.
```c=
// In this example, our customized floating format has
// four digits long exponent.
// bias = 2^(k-1) -1 = 15
// -------- Min --------------
// e = 1
// Exp = 1 - 7 = -6
e = {0, 0, 0, 1}
// ---------------------------
// -------- Max --------------
// e = 14
// Exp = 14 - 7 = 7
e = {1, 1, 1, 0}
// ---------------------------
```
* Some beginners may feel comfused about Mantissa and fraction. For clarification, **fraction** is defined as bit array in memory. On the other hand, Mantissa represents actual mathematical value.
* As for fraction, just like logarithm in high school. It is restricted in certain range.
$$
0\leq f < 1
$$
Since we only care about the range greater than 1 and less than -1 as the [figure](#Normalized_range) above, and it is always possible to modulate exponent to make Mantissa falls in certain range, the first digit behind decimal point is always **1**.
$$
1\leq Mantissa < 2
$$
```c=
// Let's consider a FP example which is composed of
// a. 1 digit sign bit
// b. 5 digit exponent
// c. 2 digit mantissa
char bit_array[] = {
0, // sign bit
1, 1, 1, 0, // exponent = 7
1, 1, 1 // fraction
};
// fraction f = 0.111 -> 1/2 + 1/4 + 1/8
// Mantissa m = 1.111 -> 1 + 1/2 + 1/4 + 1/8
// Resulting value FP = + (1 + 1/2 + 1/4 + 1/8) * 2^7
```
#### Homework
```c=
// Please implement a function which extracts three parts
// of floating point.
void print_fp_three_parts(float fp) {
// ....
}
// hint:
// 1. shift operator (>> and <<)
// 2. binary mask
// 3. According to C standard, it is illegal to conduct bit
// operation on float variable. One should use a uint32_t
// variable to carry binary information.
uint32_t convert2uint(float fp) {
uint32_t *ptr = (uint32_t *)&fp;
return *ptr;
}
```
#### Denormalized format
* Exponent is **all zero**. Exponent value is fixed to $E=1-Bias$.
* Compared to **Normalized format** above, denormalized format focuses on the range within 1 and -1.
$$-1 < FP < 1$$
Mantissa is just what fraction represents, without adding **1** before decimal point.

```c=
char bit_array[] = {
0, // sign bit
0, 0, 0, 0, // exponent is fixed E = 1 - 7 = -6
1, 1, 1 // fraction
};
// Resulting value FP = + (1/2 + 1/4 + 1/8) * 2^(-6)
```
* There are two usage of **Denormalized format**.
* Representing zero
Since Normalized format force Mantissa starts from **1**, it is impossible to represent zero. However, ability of representing zero also cause the negative zero issue. According to C standard, C compiler views negative zero just like positive zero with [few exception](https://stackoverflow.com/a/5096205/13003697).
* Gradual underflow
If you watch carefully, it is easy to observe that both Normalized format and Denormalized format split the whole real number set into multiple ranges with unequaled length. Expecially for normalized format, when representing point approaches infinity, it skips further and further. On the contrary, the distance within $(1,-1)$ gradually becomes equal.
#### Sum up

#### Rounding Error
* Small quiz
```python=
>>> print(1.01 * 3 == 3.03)
>>> # True or False?
```
* How does rounding error happen? how to solve it?
The core of floating point is trying to represent whole unlimited real number set with limited point. Thus, chances are the actual value falls into the interval between points. To make sure whole computation goes smoothly and get an relatively acceptable output, we inevitably have to make some compromise. The issue is which point to choose?
* round-to-nearest
Round the actual value to either upper or lower nearest representable point.
* round-to-even
Round the actual value to the nearest representable point which ends with '0'.
* [Decimal module](https://docs.python.org/3/library/decimal.html) in Python
## As a model designer, should I care about these shit?
* Yes, and the shit is actaully really helpful.
* [Making floating point math highly efficient for AI hardware](https://engineering.fb.com/ai-research/floating-point-math/)
* [Speeding up Deep Learning with Quantization](https://towardsdatascience.com/speeding-up-deep-learning-with-quantization-3fe3538cbb9)