---
tags: summer_training
---
# Data Structure and Algorithm
## Time Complexity Approximation
* Constant $O(1)$

The execution time of algorithm doesn't depend on input(n). The nature of the description is that it only pictures the procedure has a **fixed** duration but actual execution time varies.

    void constant_func() {
        printf("helloworld\n");
    }    

Note that hash table is the data structure that has $O(1)$ for querying.
* linear $O(n)$

Considering a function gives output of an array, it's obvious that the execution time should depend on array length.

    uint32_t get_len(int *arr, int n) {
        int sum;
        // The for-loop runs n times.
        for (int i = 0; i < n; i++) {
            sum += arr[i]
        }
    }

* n square $O(n^2)$

Now let's consider a relatively advanced function. Following is function implements addition between two square matrix.

    int *square_mtx_add(int *arr1, int *arr2, int n) {
        int output[n][n];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                output[i][j] = arr1[i*n + j] + arr2[i*n + j];
    }

* Time Complexity Approximation

In practical world, these operations often exist consecutively. Therefore, time complexity analysis is often denoted as the dominant term. Please keep in mind that when we try to realize time complexity, what we really worry about is the execution scenario in the most extreme usecase. Also coefficient (係數) means nothing in time complexity analysis.

$$
O(2n^2+n+1) \approx O(2n^2) \approx O(n^2)
$$

* **[Exercise]** Fibonacci sequence

Please analysis time complexity of following Fibonacci caculation.

     int get_fibo(int n) {
         if (n == 0 || n == 1)
             return 1;
         else
             return get_fibo(n-1) + get_fibo(n-2)
     }
     
     // O(2^n)

## Sorting
When learning algorithm, sorting plays a really important role since sorting is a common operation and we often apply the technique hidden in sorting in our program.
### Merge Sort
Merge Sort is a typical demonstration of **Divide and Conquer**. When dealing with a difficult issue, why not we just descompose it into multiple relative small componant and solve it in that level.


/* C program for Merge Sort */
#include <stdio.h> 
#include <stdlib.h> 

// Merges two subarrays of arr[]. 
// First subarray is arr[l..m] 
// Second subarray is arr[m+1..r] 
void merge(int arr[], int l, int m, int r) { 
	int i, j, k; 
	int n1 = m - l + 1; 
	int n2 = r - m; 

	/* create temp arrays */
	int L[n1], R[n2]; 

	/* Copy data to temp arrays L[] and R[] */
	for (i = 0; i < n1; i++) 
		L[i] = arr[l + i]; 
	for (j = 0; j < n2; j++) 
		R[j] = arr[m + 1 + j]; 

	/* Merge the temp arrays back into arr[l..r]*/
	i = 0; // Initial index of first subarray 
	j = 0; // Initial index of second subarray 
	k = l; // Initial index of merged subarray 
	while (i < n1 && j < n2) { 
		if (L[i] <= R[j]) { 
			arr[k] = L[i]; 
			i++; 
		} 
		else { 
			arr[k] = R[j]; 
			j++; 
		} 
		k++; 
	} 

	/* Copy the remaining elements of L[], if there 
	are any */
	while (i < n1) { 
		arr[k] = L[i]; 
		i++; 
		k++; 
	} 

	/* Copy the remaining elements of R[], if there 
	are any */
	while (j < n2) { 
		arr[k] = R[j]; 
		j++; 
		k++; 
	} 
} 

/* l is for left index and r is right index of the 
sub-array of arr to be sorted */
void mergeSort(int arr[], int l, int r) { 
	if (l < r) { 
		// Same as (l+r)/2, but avoids overflow for 
		// large l and h 
		int m = l + (r - l) / 2; 

		// Sort first and second halves 
		mergeSort(arr, l, m); 
		mergeSort(arr, m + 1, r); 

		merge(arr, l, m, r); 
	} 
} 

/* UTILITY FUNCTIONS */
/* Function to print an array */
void printArray(int A[], int size) { 
	int i; 
	for (i = 0; i < size; i++) 
		printf("%d ", A[i]); 
	printf("\n"); 
} 

/* Driver program to test above functions */
int main() { 
	int arr[] = { 12, 11, 13, 5, 6, 7 }; 
	int arr_size = sizeof(arr) / sizeof(arr[0]); 

	printf("Given array is \n"); 
	printArray(arr, arr_size); 

	mergeSort(arr, 0, arr_size - 1); 

	printf("\nSorted array is \n"); 
	printArray(arr, arr_size); 
	return 0; 
} 

#### Time complexity
First, let's consider the level of a tree. The level of a **n** binary tree has $log_2n$ depth. Now after the **divide** part, how about the conquer part.


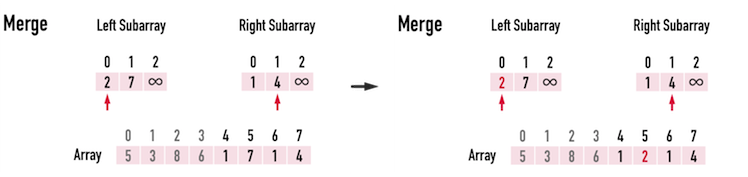
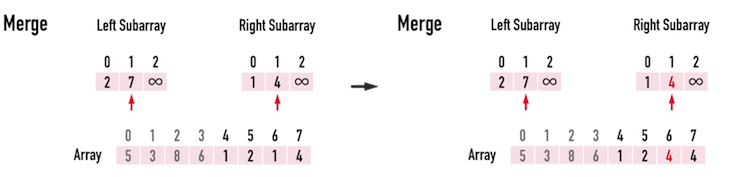
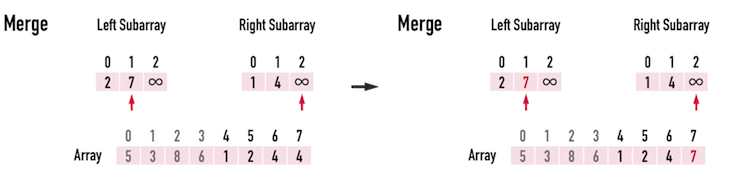
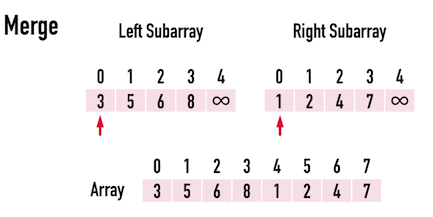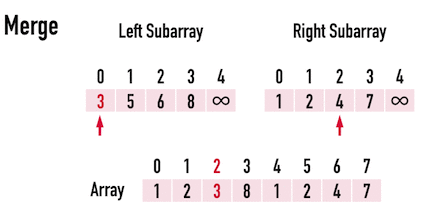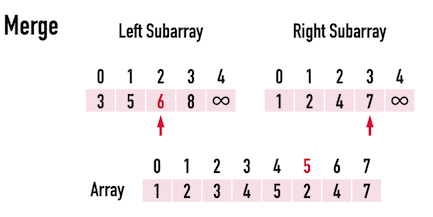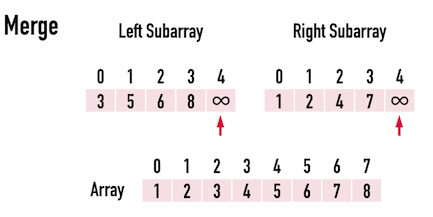
$$
Time\;Complexity =O(n\log n)
$$
> In each level every element should be iterated and there are $\log n$ levels.
> [color=#c14011]
#### Few thoughts
Recursive is **amazing** but unsecure. why?

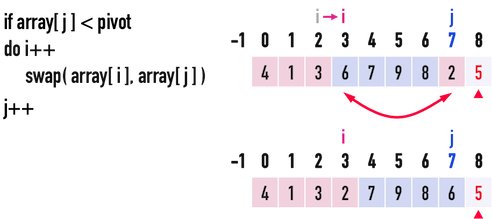
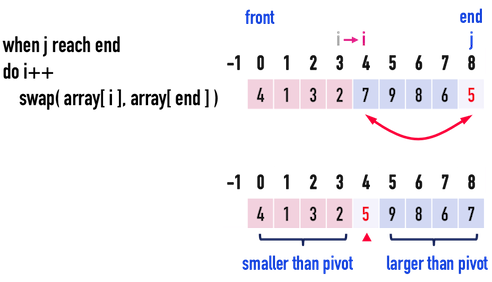
### Quick Sort
Recall that we just decribe above about **worst** condition. Quick sort is the case that has different complexity in different scenario. Let's review quick sort algorithm first. Note that the thought of **divide and conquer** is also applied in quick sort.

* Partition

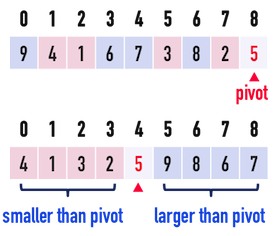
* Steps to create partition

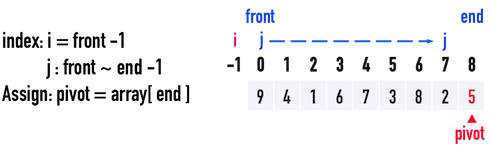
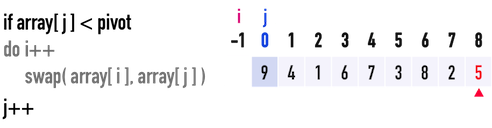
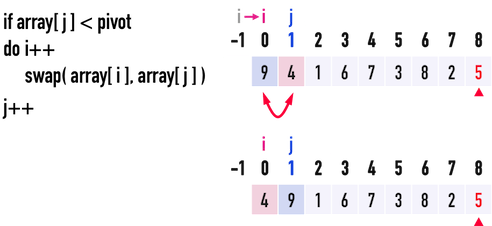
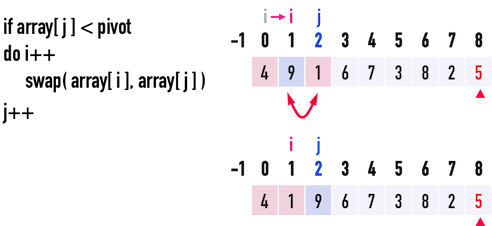
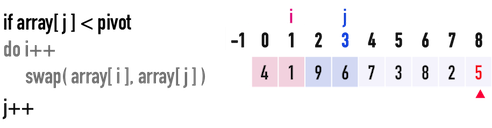
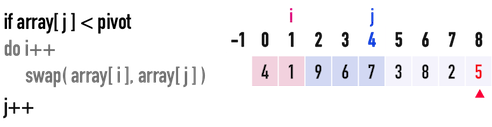
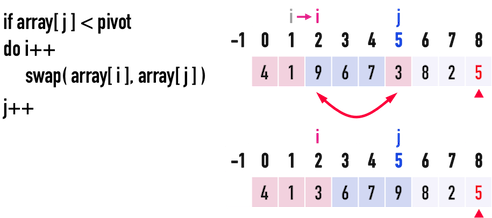
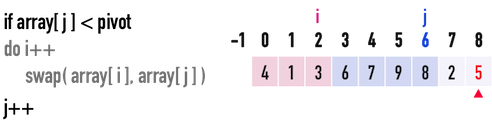
* Worst Case
What if you are sorting a array like this, and alway use the last one as pivot?

`[ 9, 8, 7, 6, 5, 4, 3, 2, 1]`
$$
Time\; Complexity\; in\; different\; cases \\
worst\; case\; O(n^2) \\
average\; case\; O(n\log n) \\
best\; case\; O(n\log n) \\
$$

## Common Data Structure
* Core idea in this data structure
* Classical application
* Please keep in mind that the key is not only that you understand high level concept. Make sure that you are able to implement from scratch.
### Stack


Stack is a simple data structure and it can be implemented with Linked List. Although you may not notice, stack is data structure that you encounter most frequently. **Scoping** in our familiar programming model is a typical stack usecase.

void foo() {
    // last scope in this example.
}
int main() {
    // highest level scope

    { 
        // sublevel scope
        // some stuff requires gardian...
        ...
        foo();
    }
    return 0;
}

Another common usecase is DFS in tree traversing. we'll leave it until tree section.

### Queue


Queue is another fundamental data structure. It often plays core in communication system, for instance network package sending and recieving in Linux kernel network stack.


Another classical usecase is [Producer and Consumer model](https://en.wikipedia.org/wiki/Producer%E2%80%93consumer_problem) in [Design Patten](https://en.wikipedia.org/wiki/Software_design_pattern).

Things even get more complex across multiple machines.

### Tree
Tree is wellknown data structure as well. Since it is a [special case](https://www.geeksforgeeks.org/difference-between-graph-and-tree/) in graph, the property that graph has is all suitable in tree. In Linux, tree is almost everywhere including PID tree and FileSystem.


The relation of Linux FileSystem and tree has two perspective.
* Layout of files
Linux organizes the files in tree format as the image I mention above. There are two types of file in Linux.
- Directory
- Normal file (other than Directory)
* Implementation
Filesystem is basically a huge Hash table whose key is file path and value is a bunch of binary object on disk.
+ Ext2
+ [Btrfs](https://en.wikipedia.org/wiki/Btrfs)
+ FAT32
#### Strong bonding between Algorithm and Data structure
Although data structure and algothim seems two seperable concepts, they are actually tied close unexpectedly.

#### **[Exercise]** lse

Please implement a program similar to `ls` which takes file path as an argument.
+ input regular file

> output the file size.

+ input directory file

> Traverse the directory until leaf and output the accumulated file size.

### Heap
In tree, we often store our data in each node. Here in heap, we focus on storing numbers in nodes following certain rule.

#### Application
+ [Huffman code (Compression)](https://www.techiedelight.com/huffman-coding/)
+ [Priority queue and interrupts handling](https://0xax.gitbooks.io/linux-insides/content/Interrupts/linux-interrupts-9.html)
+ [A* algorithm]()
## Reference
* [Queueing in the Linux Network Stack](https://www.coverfire.com/articles/queueing-in-the-linux-network-stack/)
* [Atomics & lock-free data structures c++](https://superchargedcomputing.com/2018/03/25/atomics-and-lockfree-data-structures-in-c/)
* [KubeMQ Docs](https://docs.kubemq.io/learn/message-patterns/queue)
* [Ext2 filesystem in Linux](https://en.wikipedia.org/wiki/Ext2)
* [Breaking Down Breadth-First Search](https://medium.com/basecs/breaking-down-breadth-first-search-cebe696709d9)
* [Introduction to Priority Queue using Binary heap](https://www.techiedelight.com/introduction-priority-queues-using-binary-heaps/)