# 圖 (Graph)

## 圖的表示方式

1. **鄰接矩陣 (Adjacent Matrix)**

利用矩陣來儲存圖中的頂點連接情形

使用鄰接矩陣處理的好處為實作上很容易，缺點是無法處理重邊（重邊：即同一對頂點相連接的邊，在有像圖中，還要求方向相同），在無向圖中，因為 **(Vi,Vj) = (Vj,Vi)** 所以從左上到右下把無向圖的鄰接矩陣分為兩個三角形後，這兩個三角形會對稱，只需要儲存其中一個三角形即可

因為矩陣共有 **|V|\*\*2** 項，所以建立鄰接矩陣時的時間和空間複雜度都會是 **O(|V|\*\*2)**，不過好處是查詢兩點間是否存在邊時，可以利用索引值直接存取對應資料，只需要 **O(1)**，修改時也只需要 **O(1)**

綜合來說，鄰接矩陣在建立時複雜度較大，而在日後存取和修改時較快。

另外如果邊上有權重，用鄰接矩陣來表示時，矩陣中存放的就不再是 0 和 1，而是對應邊的權重。

2. **鄰接列表 (Adjacent List)**

用對應個頂點的 **陣列 (Array)** 或 **鏈結串列 (Linked List)** 來紀錄點上的所有邊

舉例：

| Node | List |
| -------- | -------- |
| A | ->B->C->D |
| B | ->A->C |
| C | ->B->A->D |
| D | ->A->C |

建立鄰接列表的時間和空間複雜度都是 O(|V| + |E|)，因為總共有V個row（每個row都是一個列表），而所有列表的長度總和為 **2|E|** ，因此要建立起鏈結串列的開頭，並儲存全部共 **2|E|** 筆資料，就需要 **O(|V| + 2|E|) = O(|V| + |E|)** 的空間

若邊上有權重，則鏈結串列上的節點node會是一個結構，裡面儲存了邊連到頂點與邊上的權重，比如 A -> B,2 代表存在邊 (A,B)，其權重為 2

3. **前向星 (Forward Star)**

前向星是指用同一個陣列來儲存所有邊，並記錄每一個邊的起點和終點


考量到使用上的效率和簡便程度，最常用來儲存圖的資料結構是 **鄰接矩陣**和**鄰接列表**。

## 三種圖的比較

1. 鄰接矩陣 (Adjacent Matrix)

- 利用矩陣儲存圖中的頂點連接情形
- 優點：查詢和更新快，O(1)
- 缺點：浪費空間，O(|V|**2)
- 適用於**稠密**的圖：邊數 |E| ~ 最大可能數 |V|**2

2. 鄰接列表 (Adjacent List)

- 每項頂點皆有個別的陣列或鏈結串列來記錄該點上的所有邊
- 優點：節省空間，O(|V|+|E|)
- 缺點：查詢和新增都比鄰接矩陣花時間
- 適用於**稀疏**的圖：邊數 |E| ~ 最大可能邊數 |V|**2

3. 前向星 (Forward Star)

- 把邊都儲存在同一個陣列裡，並加以排序

一個 **稠密** 的圖是指圖中的頂點幾乎都與所有頂點有邊相連，**稀疏** 的圖中邊數很少，如果使用矩陣來儲存稀疏的圖，就會浪費空間再大量的 **0** 上

## 圖的分類

### 簡單圖 (Simple Graph)

簡單圖的定義如下：

1. 不包含重邊，即 **ei = ej & i != j**
2. 不包含自環，即 **e(vi,vi)**

### 有向無環圖 (Directed Acyclic Graph, DAG)

有向無環圖就是不包含 **環** 的圖，節點之間不會形成循環，即從任意一點出發，都不會回到原先的節點

要對一個圖進行 **拓墣排序** 的前提是該圖為一個 **有向無環圖**

### 二分圖 (Bipartite Graph)

二分圖代表一個無向圖中，可以把所有頂點分成兩個集合 V1、V2，使得所有邊 e(V1,V2)連接的V1、V2必定不在同一集合內

#### 無向圖的黑白染色

要分辨一個無向圖是否為二分圖，就必須遍歷該圖，也就是指定一個 **黑點**，把 **黑點** 相鄰的點都塗成 **白色**，再把白點相鄰的點都塗成黑色，依此類推，直到整張圖的每個節點都是黑色或是白色其中一種後，如果該無向圖為一 **二分圖**，圖中就不會有任何一個邊連接著 **黑點和黑點** 或 **白點和白點**，也就是說，圖中的黑點不會和黑點相鄰，白點不會和白點相鄰。

### 平面圖 (Planar Graph)

根據尤拉公式 (Euler Formula)：

**|V| + |E| + F = 2**

上述公式代表著，頂點個數減掉邊的個數，再加上區塊個數後會等於 **2**

舉例有一三角形，總共有 3個邊、3個頂點和 2 個區塊（三角形內部和外部），符合公式 3 - 3 + 2 = 2

### 連通圖 (Connected Graph)

連通圖分為兩種，一種為 **無向聯通圖**，一種為 **有向聯通圖**

#### 無向圖的聯通圖 (Undirected Connected Graph)

無向圖的聯通圖中，任兩點間一定存在一個路徑，否則就視為不聯通

#### 有向圖的聯通圖 (Directed Connected Graph)

有向圖的聯通圖中，因為邊是單向的，所以與無向圖相比，較不容易形成聯通圖，並且將聯通圖分為以下三種：

1. 強聯通 (Strongly Connected)：任兩點間必存在路徑
2. 弱聯通 (Weakly Connected)：將該圖化為無向圖後，任兩點間必存在路徑
3. 不聯通（Disconnected）：非強聯通，也非弱聯通的圖

#### 強聯通元件 (Strong Connected Component) SCC


一張圖可以被視為一些強聯通元件的集合，每個強聯通元件的內部都是強聯通的，比如上圖中，左邊四個頂點是強聯通元件，右邊四個頂點也是強聯通元件

### 完全圖 (Complete Graph)

完全圖是指圖中的任意頂點兩兩之間一定會有邊

無向完全圖，其邊數是：**|E| = |V| \* (|V| - 1) / 2**

有向圖中，因為 **A指向B** 和 **B指向A** 的邊是不同的，因此完全圖的邊數是：**|E| = |V| \* (|V| - 1)**

## AOV網路、AOE網路與拓墣排序

### AOV網路 (Activity on vertex)

AOV網路使用**頂點**來表示活動，表示的是個活動之間的發生順序

AOV網路是一個**有相無環圖(Directed Acyclic Graph)**

舉例，如若存在邊 e(vi,vj)，就代表只有辦完 vi 的活動後，才能辦理 vj 的活動

### 拓僕排序 (Topological Sort)

拓墣排序是針對**有相無環圖**或者**AOV(E)網路**，找到所有頂點的排列順序，使頂點和邊符合拓墣排序的順序關係

舉例：如若存在邊 e(a,b)，在拓墣排序後的順序中，a 就一定會在 b 之前

### AOV網路的拓墣排序

想要得到一個AOV網路的拓墣排序，須透過如下步驟進行

1. 從AOV網路中的其中一個入度(in_degree)的頂點出發，
2. 把該頂點的所有相鄰邊刪除
3. 重複步驟 A、B，直到找不到入度為 **0** 的點

### AOE網路 (Activity on Edge)

AOE網路使用**邊**來表示活動(不同於AOV網路)，邊上的權重代表該活動完成所需要花費的時間，頂點則代表**事件(Event)**

AOE網路與AOV網路同樣都為**有向無環圖(Directed Acyclic Graph)**

## AOE網路中的關鍵路徑 (Critical Path)

AOE網路的關鍵路徑分為兩種：

1. 最早開始時間 (Early time)

最早開始時間可表示為：E(Vj) = max(E(Vj),E(Vi) + w(Vi,Vj))
定義：E(Vi) = 前一節點、E(Vj) = 當前節點

2. 最晚開始時間 (Late Time)

最晚開始時間需要最早開始時間的的 **最終和**，並且所有節點的時間必須要初始化為最早開始時間，利用**反向拓墣排序**逐一計算，也就是按照拓墣排序的順序反向計算回去

最晚開始時間可表示為：E(Vj) = min(E(Vj),E(Vi) - w(Vi,Vj))
定義：E(Vi) = 前一節點、E(Vj) = 當前節點

## 最小生成樹 (MST)

貪婪演算法可以解決的一個問題就是找到一張圖中的最小生成樹(minimum spanning tree)。

### 樹、生成樹與最小生成樹

我們之前提到資料結構中的樹是有根樹(rooted tree)，也就是樹中有一個根節點。但其實樹不一定都有根節點，只要任意兩節點都有(也只有)一條邊相連的圖就稱作樹。

###### 圖片來源：[維基百科](https://en.wikipedia.org/wiki/Tree_(graph_theory))


而一個圖中的生成樹(spanning tree)，就是指連接該圖所有節點的樹，一個圖可能有不只一個生成樹。而最小生成樹就是指在有權圖中，權重總和最小的生成樹。例如下圖中綠色的部分，就是這個圖的最小生成樹。

###### 圖片來源：[維基百科](https://zh.wikipedia.org/wiki/%E6%99%AE%E6%9E%97%E5%A7%86%E7%AE%97%E6%B3%95)


那麼最小生成樹可以解決什麼問題呢？其中一種最直接的應用是線路設計，例如沿著街道(邊)為住家(節點)架設電纜的情境，最小生成樹可以作為成本最低的路徑。另外，最小生成樹也可以用來作為困難問題的近似解，或間接應用在人臉或字跡辨識等技術中。

### 貪婪解法

有許多演算法可以找到一個圖中的最小生成樹，下面寫到的幾種都是屬於貪婪演算法。這幾種方法雖然關注點或出發點不同，但同樣都是用貪婪策略，每一階段都選擇局部最佳解，以達到最終的整體最佳解。也表現出之前提到的，一個問題可能以多種貪婪演算法解決。

#### Prim's algorithm

普林演算法的策略與先前提到尋找最短路徑的Dijkstra演算法非常相似(事實上這個演算法也被Dijkstra再次發現與發表，所以也稱為Prim–Dijkstra algorithm)，它的作法是：

1. 先將任意節點加入到樹之中。

2. 選擇與樹距離最近的節點，加入到樹中，反覆此步驟直到所有節點均在樹中，即為最小生成樹。

以上方的圖為例，如果一開始選擇G節點，接下來將最近的節點E加入樹中，接下來將與G或E最近的節點C加入...以此類推，也就是每一階段樹都會納入距離最近的節點、增加一條邊，直到連接所有的節點。

#### Kruskal's algorithm

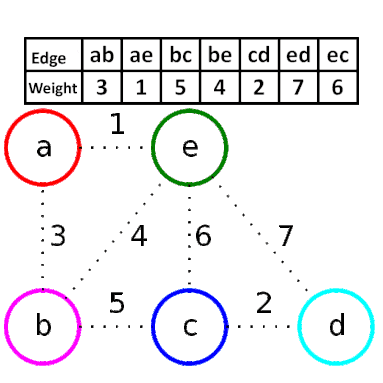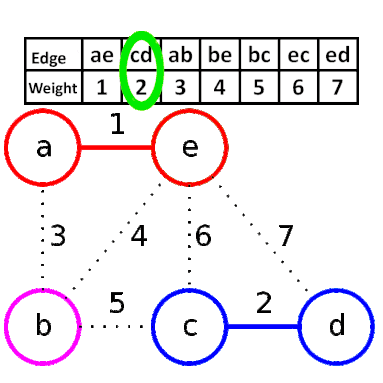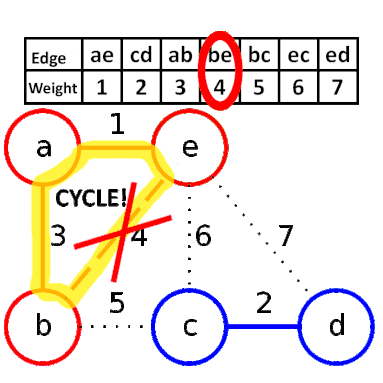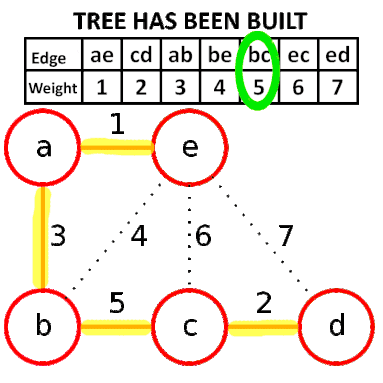
Kruskal演算法的方式是從所有邊中，反覆選擇最短的邊，它的步驟是：

1. 將所有的邊依照權重由小到大排序。

2. 從最小開始，選擇不會形成環的邊，直到連接所有節點。

如下圖，先將邊排序，依序選擇，其中邊be即是因為會形成環所以不選。


#### Borůvka's algorithm

Borůvka演算法則是利用節點的最短邊得出多棵樹，再將樹以最短邊相連：

1. 找尋每個節點的最短邊，可以重複選擇(例如下圖AC同時是A節點和C節點的最短邊)，如此一來會形成幾個不相連的樹，如下圖中經過第一步驟後得到AC、BD、EF等不同的樹，以不同顏色標示。
2. 以同樣的方式，反覆找尋每個樹的最短邊，每次操作樹的數量都會減少，直到最終只剩下一個樹即為最小生成樹。

### 圖論技巧

#### 二維矩陣的展平

二維矩陣轉換為一維矩陣的操作稱為 **Flatten (展平)**

二維矩陣座標轉換公式：

**公式:**
define node = 二維矩陣轉換過後的一維矩陣座標
define n = 10 => rows = 10 , cols = 10
node = y * cols + x
x = node / cols
y = node % cols

**證明:**
x = 0 , y = 0 => 0
x = 1 , y = 1 => 11
x = 3 , y = 3 => 33
x = 5 , y = 7 => 57

#### 二維矩陣的多方向遍歷

二維矩陣多方向遍歷可以用當前坐標來計算差值，藉此算出鄰居座標，具體技巧可以使用陣列來儲存 **4個方向** 或 **8個方向** 的差值，看題目具體給定

# 偽代碼
four_direction_maps = [[-1,0],[0,-1],[1,0],[0,1]]
eight_direction_maps = [[-1,0],[0,-1],[1,0],[0,1],[1,1],[-1,-1],[-1,1],[1,-1]]

for _x,_y in direction_maps:
    # 新的 x y 座標值
    new_x = x + _x
    new_y = y + _y
    
    if new_x < 0 or new_y < 0 or new_x >= rows or new_y >= cols: # 確認是否有超出邊界，有超出邊界則跳過
        continue
    

##### 參考資料
###### 圖片來源：[維基百科](https://en.wikipedia.org/wiki/Bor%C5%AFvka%27s_algorithm)


[Minimum Spanning Tree：Prim's Algorithm](http://alrightchiu.github.io/SecondRound/minimum-spanning-treeprims-algorithm.html)