• Python
• Chocolate
• Anaconda
• Github + Google (colab)
• Brewed coffee
• Good Will!

1. social skills!!!
   • documentation
   • team members
   • clients

2. Reproducibility/Replicability

3. Data analysis \(\neq\) Stats on a MacBook

collaboration

• Slack/MS Teams/Discord is not enough!
• team, team, team

1. "I work alone. I don't care"

• you collaborate with yourself
• your future self will need
  • documentation
  • debugging

you always need to collaborate

• looking for advice
  • blogs: bloggers share knowledge
  • books: authors share knowledge
• beta-testing
  • you are not the best programmer to test your own code
• why don't you ask for collaboration?!?!

2. "I work on a team"

• your future self is part of the same team
  • smart member
  • your future self will need documentation
• you (your code) have to interact with others
  • documentation
  • README file
  • end-user
    • how to run the code?
  • developer
    • how to start working on the code?

Reproducibility

• Reproducibility PI Manifesto :: Lorena A. Barba Group
  • slides
• Reproducible Science. PhD Training Programme at BSC

Data Science Template

• Cookiecutter Data Science
  • You will thank you

Install the template

• data science template

Directory Structure

• structure

Data is immutable

• Don't ever edit your raw data
  • especially not manually…
  • …and especially not in Excel
• Don't overwrite your raw data
• Treat the data (and its format) as immutable.
• data folder in .gitignore

Data version control

• databases
• Data Version Control · DVC
• Git Large File Storage
• AWS Amazon Simple Storage Service (S3)

• Data science project template
  • templates
  • documentation
  • README files
  • LICENSE
  • semantic versioning
  • collaboration
    • issues
    • Pull Requests

• tools
  • Github
  • CookieCutter
    • See also: Copier
  • documentation
    • Sphinx
    • MkDocs

Template for Workflows

• Snakemake template

AI Ethics

• Deon: An ethics checklist for data scientists

jupyter notebook

• Project Jupyter | Home
  • Try it online

Deployment

• according to wikipedia

  Software deployment is all of the activities that make a software system available for use.

notebooks are just for exploration

• I don't like notebooks - Joel Grus
• well…
• let's deploy jupyter notebooks

papermill + nbconvert

• run notebooks from command line
  • parameterize
    • from command line
    • from yaml config file
  • inject variables into the notebook
    • cell tagged parameters
• See how Netflix uses papermill

papermill + nbconvert

• jupyter notebook \(\rightarrow\) webpage (html)
• how to

• further reading:

  • Automated Report Generation with Papermill: Part 1 - Practical Business Python
  • Automated Report Generation with Papermill: Part 2 - Practical Business Python

• cons

  • nbconvert
    • no interactivity
    • javascript running in the browser

webapps / Dashboarding

• voilà
  • voilà: notebook running on heroku
• streamlit
  • GitHub - alonsosilvaallende/streamlit-test
  • Streamlit-Urbana
• anvil
  • local notebook to a webapp
    • simple tutorial
  • webapp with user registration

• Data Preparation
• Exploratory Data Analysis
• Visualization
• Features Engeneering
• Features Selection
• Modelling
• Deployment

Data Preparation

Raw Data

• structured data: data matrix
• graph: web and social networks
• spatial data
• time series
  • sensors data
  • stock exchange data
• unstructured data:
  • text
  • images

Data Cleaning

• extract data with different formats
  • excel, json, csv, pdf, jpg, mp4, etc.
• evaluation of data accuracy and reliability
  • presence of missing values
  • outliers
  • inconsitencies
  • level of noise

Data Consolidation

• consistency across different data sources
• consistency of units
• consistency of scales
• consistency of file, folder names, etc..
• data testing

Exploratory Data Analysis

Problem identification

• analysis before modelling
• the objective is to understand the problem in order to generate testable hypotheses
• clear, concise and measurable
• define
  • target/label (dependent variable)
  • features (indepent variables)
• crucial to select the right class of algorithms

Basic Statistics

• describe dimensions
• type of distributions
• descriptive statistics
  • mean, median, mode, std
• correlation between features
• relationships and pattern due to the structure of the data

Quintessential rules

Data visualization is a key part of communicating your work to others

• less is more
  • check properly the type of graph,
    with a graph you are able to tell a story
  • check dimension of axes marks
• reduce the clutter
  • avoid unecessary or distracting visual elements
    • ornametal shading, dark gridlines
    • 3D when not mandatory

Tips

A color can be defined using three components (aka RGB channels)

• hue: component that distinguishes “different colors”
  • vary hue to distinguish categorical data
• saturation: the colorfulness
  • vary saturation to stratify the plot
• luminance: how much light is emitted, ranging from black to white
  • vary luminance to rages/bins in numerical data

Sequential palettes

A sequential palette ranges between two colours ranging from a lighter shade to a darker one. Same or similar hue are used and saturation varies.

Viridis palette

• is implemented using blues and yellow sequences (and avoiding reds), in order to increase the readability for the visualizations
  
• When to use it:
  • intended to represent numeric values
  • range of the data without meaningful midponint, no highlighting a specific value

Diverging palettes

A diverging palettes can be created by combining two sequential palettes (e.g. join them at the light colors and then let them diverge to different dark colors)

Icefire palette

• When to use it:
  • two hue are used indicating a division, such as positive and negative values or booleans
  • there is a value of importance around which the data are to be compared

Visualization packages

• Matplotlib
  • used for basic graph plotting like line charts, bar graphs
  • it works with datasets and arrays
  • is more customizable and pairs well with Pandas and Numpy

• Seaborn
  • can perform complex visualizations with fewer commands
  • It works with entire datasets treated as solitary unit
  • it contains more inbuilt theme, and it is considerably more organized and functional than Matplotlib and treats the entire dataset as a solitary unit

Hands-on

• EDA pandas profiling
• Data preparation: Anime dataset notebook
  • Data Consolidation
  • EDA

ML WorkFlow

Process of solving a practical problem by

1. gathering a dataset
2. building a statistical model on that dataset

Machines don't learn
A learning machine finds a mathematical formula, which, when applied to a collections of input produces the desired output.
If you distort your data inputs, the output is very likely to become completely wrong

Why the name Machine Learning?

Arthur Lee Samuel was an American pioneer in the field of computer gaming and artificial intelligence.

He popularized the term "machine learning" in 1959 at IBM.

…Marketing reason…

Two Types of Learning

Supervised Learning

The dataset is a collection of labeled examples
\(\{(x_{i}, y_{i})\}_{i=1}^{N}\)
\(x_{i}, i=1, \dots, N\) is called feature vector
\(y_{i}, i=1, \dots, N\) is called label or target

Goal: use a dataset to produce a model that takes a feature vector as input and outputs informations that allows deducing the label for this feature vector

Unsupervised Learning

The dataset id a collection of unlabeled exaples
\(\{(x_{i})\}_{i=1}^{N}\)

Goal: create a model that takes a feature vector as input and either trasforms it into another vector or into a value that can be used to solve a practical problem

Classification Problem

Classification predictive modeling is the task of approximating a mapping function from input variables to discrete output variables.

A discrete output variable is a category, such as a boolean variable.

Example: Spam detection

Regression Problem

Regression predictive modeling is the task of approximating a mapping function from input variables to a continuous output variable.

A continuous output variable is a real-value, such as an integer or floating point value.

Example: House price prediction

Machine Learning Map

https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html

Scikit-Learn

https://scikit-learn.org

Linear Regression

\(\{(\textbf{x}_{i}, y_{i})\}_{i=1}^{N}\)

\(\textbf{x}_{i}\) D-dimensional feature vector of sample \(i=1, \dots, N\)

\(y_{i}\in \mathbb{R}\) \(i=1, \dots, N\), \(x_{i}^{(j)}\in \mathbb{R},\; j=1,\dots, D\)

Model:
\[f_{\textbf{w}, b}(\textbf{x})= \textbf{wx} +b, \; \\ \textbf{w}\;\mbox{is a D-dimesional vector of parameter}, b\in \mathbb{R}\]

Goal:
predict the unknown \(y\) for a given \(\textbf{x}\)
\[y = f_{\textbf{w}, b}(\textbf{x})\] find the best set of parameters \((\textbf{w}^{*}, b^{*})\)

How:
Minimize the objective function
\[\dfrac{1}{N}\sum_{i=1}^{N}(f_{\textbf{w}, b}(\textbf{x}_{i})-y_{i})^{2}\]

Logistic Regression

\(\{(\textbf{x}_{i}, y_{i})\}_{i=1}^{N}\)

\(\textbf{x}_{i}\) D-dimensional feature vector of sample \(i=1, \dots, N\)

\(y_{i}\in \{0,1\}\) \(i=1, \dots, N\), \(x_{i}^{(j)}\in \mathbb{R},\; j=1,\dots, D\)

Model:
\[f_{\textbf{w}, b}(\textbf{x})= \dfrac{1}{1+\exp(-(\textbf{wx}+b))}\]
where \(\textbf{w}\) is a D-dimesional vector of parameter; \(b\in \mathbb{R}\)

Goal: maximize the likelihood of the training set
\[L_{\textbf{w}, b}= \prod_{i=1}^{N} f_{\textbf{w}, b}(\textbf{x}_{i})^{y_{i}} (1- f_{\textbf{w}, b}(\textbf{x}_{i}))^{(1-y_{i})}\]
When \(y_{i}=1\) then \(f_{\textbf{w}, b}(\textbf{x})\)
When \(y_{i}=0\) then \((1- f_{\textbf{w}, b}(\textbf{x}))\)

No close solution, use numerical optimization via gradient descent

Feature Engineering

Problem of traforming raw data into a dataset

Everything measurable can be used as a feature

Define features with high predictive power

Feature creation

• creativity
• domain knowledge
• aggregation: define new features s.a. sum, product, linear combination, power, lags in time
• binning: from numerical data to categorical data
• encoding: from categorical data to numerical data
• normalization: reduce to same range, avoid numerical overflow

Feature Validation

• Missing data
  • data imputation techiques
• Imbalance data
  • algorithm based techniques: oversampling minority class using synthetic examples (SMOTE)

Choose the right algo for your problem

• Try all algos
• Explainability: black-box issue
• Nonlinearity of the data
• Number of features and examples

Splitting Techniques

• Training set \(\rightarrow\) built your model
  
• Holdout sets:
  
  • Validation set \(\rightarrow\) model selection and hyperparameter tuning
    
  • Test set \(\rightarrow\) evaluation

The rule of thumb
70% training set, 15% validation set, 15% test set

On Big Data: 95% training set, 2.5% validation set, 2.5% test set

Model Performace Visualization

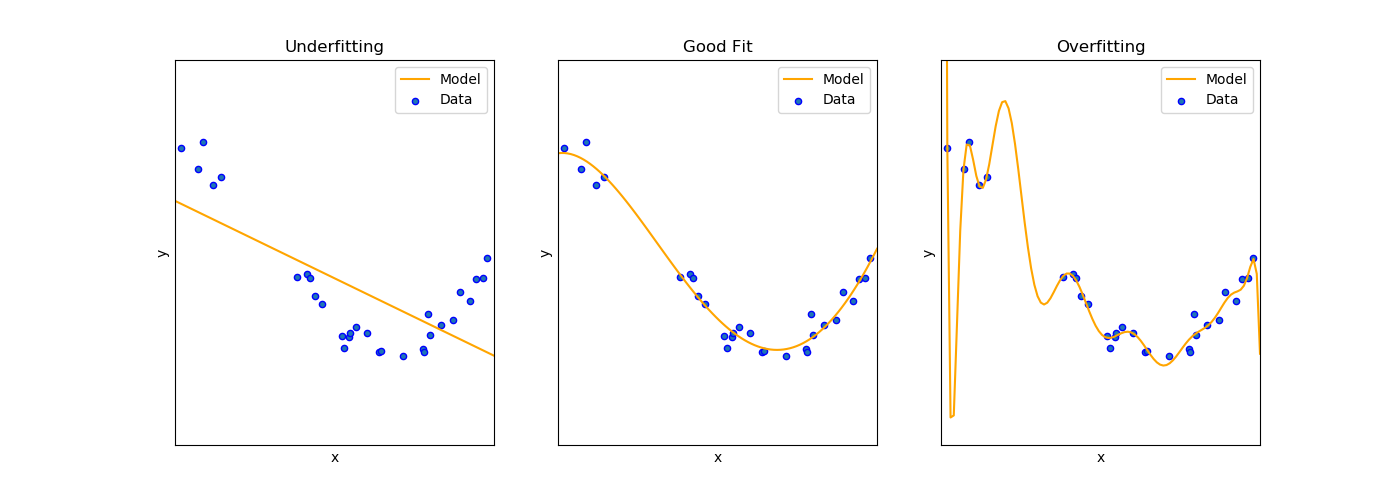
Model Performace

Overfitting

• high variance
• models the training set too well
• learns detail and noise in the training data and it negatively impacts the performance of the model on new data
  • probs: the models ability of the model to generalize

When:

• nonlinear model, flexibility when learning a target function

How to solve:

• try simpler model
• dimensionality reduction
• regularization

Underfitting

• high bias
• can neither model the training data nor generalize to new data
• probs: poor performance on the training data
• how to solve:
  • increase the algo complexity
  • engineer fetures with higher predictive power

Model Performance Metrics i

Qst: How good is my model on unseen data?

Linear regression metrics examples

• Mean squared error
  \(MSE=\dfrac{1}{N}\sum_{i=1}^{N}(y_{i}- \hat{y}_{i})^{2}\)

  • \(MSE(test)>>MSE(train)\rightarrow \mbox{Overfitting}\)

• Coefficient of determination
  \(R^{2}=1-\dfrac{\sum_{i=1}^{N}(y_{i}- \hat{y}_{i})^{2}}{mean(y_{i})}\)
  indication of the goodness of fit of a set of predictions to the actual values

Model Performance Metrics ii

Qst: How good is my model on unseen data?

Classification Metrics Example

• classification accuracy:
  ratio number of correct predictions on all predictions made
• confusion matrix
  table presents predictions on the x-axis and accuracy outcomes on the y-axis

Improve Model Performace

hyperparameter tuning
model configuration argument specified by the developer to guide the learning process for a specific dataset

• grid search:
  define a search space as a grid of hyperparameter values and evaluate every position in the grid

cross validation

• k-fold cross validation
• stratified cross validation
• rolling cross validation (time series)

Hands-on

1. exploratory data analysis

colab

• pandas-profiling
  • Titanic
  • 1978 Automobile dataset
  • Census Dataset
  • more examples

2. scikit-learn (Colab)

colab

• linear regression

colab

• logistic regression

project template

• Cookiecutter data science

• Data Consolidation
  • great-expectation
• EDA
  • pandas profiling
• Visualization
  • understand types of plots
  • matplotlib cheatsheet
• Choosing the right estimator, from scikit-learn
• RISE slides in jupyter notebook

• a BIG thanks to José Carlos Carrasco Jimenez
• CINECA course

Thanks to all the contributors

• learning
  • Machine Learning Mastery's FAQ
• tutorials
  • scikit-learn
  • Machine Learning Mastery
• books
  • Fluent in Python
    • Luciano Ramhamallo
  • The hundred-page machine learning book
    • Andriy Burkov
  • Machine Learning with PyTorch and Scikit-learn
    • Sebastian Raachka