# Merkle trees on Algorand
## Overview
A **Merkle tree** is a tree data structure (typically binary) in which every leaf node stores a cryptographic hash of a data block, and every non-leaf node stores a cryptographic hash of the joint of its child nodes. This structure allows efficient and secure verification of the contents of large data structures.
From Wikipedia:
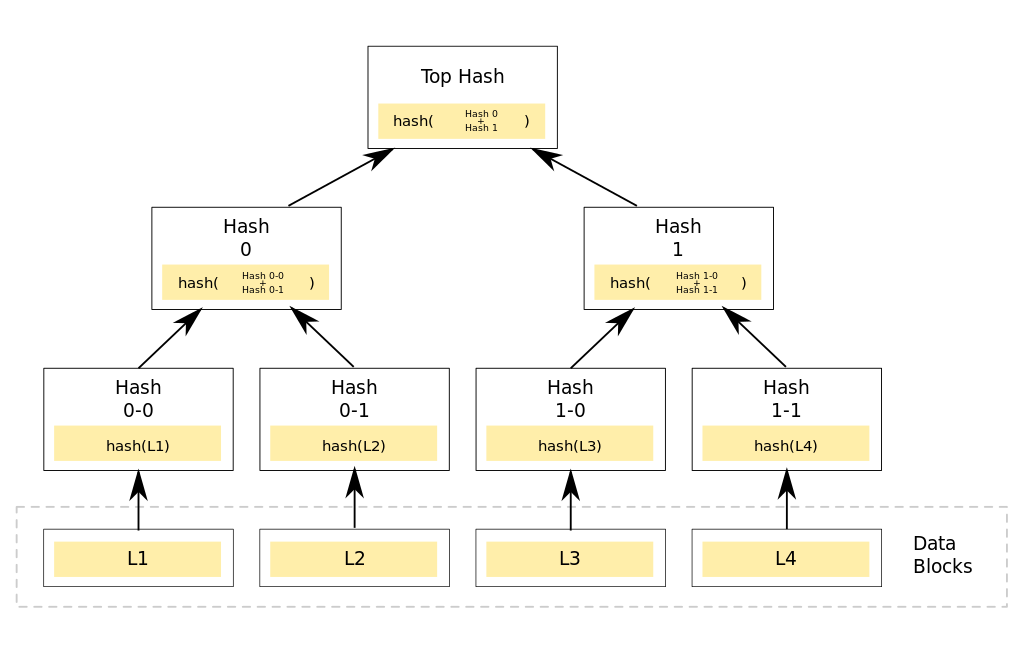
In this solution, we will demonstrate how to create and use Merkle trees using Algorand's **Smart Contracts** generated with **PyTeal** (TEAL v5).
### Design overview
#### State
Our smart-contract holds 2 global state variables:
1. **Root** - a byte slice holding the Top Hash of the tree.
2. **Size** - the number of elements in the tree.
At the beginning, `Size` is set to `0` and `Root` is computed as if the tree leaves are all hashes of empty byte slices (`e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855`).
This means that the `Root` value depends on the tree height.
#### Operations
Our Merkle tree supports 3 operations:
1. **append** - add a new data block to the end of the data sequence.
2. **verify** - verify that a data block is stored in the tree.
3. **update** - update an existent data block.
The above operations expects to receive input via the application arguments array, and all share the same schematics:
1. First argument: *command-name* - **append**, **verify** or **update**
2. Second argument: *value* - the value we wish to append/verify/update
3. Third argument and so on: *sibling1*, *sibling2*... - a list of siblings in the tree. More details below.
In addition, the **update** command also expects the last argument to be the new value to update.
##### - append command
This operation expects to receive the new data block to append, and its siblings along the path to the root. For example in the above diagram, in order to append `L1` (assuming the tree is empty) the user would provide `L1`, `Hash 0-1` and `Hash 1`.
The smart-contract will verify the position of `L1` is indeed empty and will then update the `Root` with the new value and increment the `Size`.
##### - verify command
Similar to the **append** operation, **verify** expects a value and siblings.
For example in the above diagram, in order to verify `L1` the user would provide `L1`, `Hash 0-1` and `Hash 1`.
The smart-contract will verify the position of `L1` actually holds its expected data block.
##### - update command
This operation can be thought of as a composition of the above operations.
In this case 2 values are expected: **old** value and **new** value.
The smart-contract will first verify the **old** value is in the correct position in the tree and will then compute and update the `Root` using the **new** value.
#### Passing the list of siblings
As mentioned above, all three commands expect to receive a list of siblings where each sibling is a byte-slice containing the hash value of its node in the tree.
Since Merkle trees are binary, we need to mark each sibling if it's **right** or **left**.
To do so, each sibling will hold its orientation as the first byte of the byte slice: `0xaa` for right and `0xbb` for left.
The first sibling in the list is the `1st` order sibling, the second is the `2nd` order (i.e. sibling of parent) etc.
With this method we assure that the position of value to append/verify/update is deterministic.
## PyTeal code
Now, let's get into the actual implementation.
We'll be using `PyTeal` to generate a `TEAL v5` script that will be executed on the `AVM 1.0` as a smart-contract.
### Helpful subroutines
Since computing the root is core, we'll introduce a TEAL subroutine just for that:
```python
@Subroutine(TealType.bytes)
def calc_root(init_value: Expr):
i = ScratchVar(TealType.uint64)
result = ScratchVar(TealType.bytes)
return Seq([
result.store(init_value),
For(i.store(Int(FIRST_SIBLING_INDEX)), i.load() <= Int(LAST_SIBLING_INDEX), i.store(i.load() + Int(1))).Do(
If(Substring(Txn.application_args[i.load()], Int(0), Int(1)) == Bytes('base16', 'aa')).Then(
result.store(
Sha256(
Concat(
result.load(),
Substring(Txn.application_args[i.load()], Int(1), Int(33))
)
)
)
).Else(
result.store(
Sha256(
Concat(
Substring(Txn.application_args[i.load()], Int(1), Int(33)),
result.load()
)
)
)
)
),
result.load()
])
```
`calc_root` simply iterates over the list of siblings, concatenates them according to each orientation and hash. The `init_value` is a TEAL Expression that evaluates to the hash of leaf value we wish the start our computation from.
Note that the `For` loop boundaries are constant: `FIRST_SIBLING_INDEX` which is set to `2` and the `LAST_SIBLING_INDEX` which is set to `FIRST_SIBLING_INDEX + TREE_HEIGHT - 1`.
The next subroutine is for computing the initial `Root` when the tree is empty:
```python
@Subroutine(TealType.bytes)
def calc_init_root(tree_height: Expr):
i = ScratchVar(TealType.uint64)
result = ScratchVar(TealType.bytes)
return Seq([
result.store(Sha256(Bytes(''))),
For(i.store(Int(0)), i.load() < tree_height, i.store(i.load() + Int(1))).Do(
result.store(Sha256(Concat(result.load(), result.load())))
),
result.load()
])
```
That will be used by the creation sequence:
```python
on_creation = Seq([
App.globalPut(Bytes('Root'), calc_init_root(Int(TREE_HEIGHT))), # init root
App.globalPut(Bytes('Size'), Int(0)), # init size
Approve()
])
```
#### append sequence
The **append** sequence first validates that the correct number of application arguments were received and that the value to append is not an empty byte-slice.
It then validates that the position (derived from the siblings' orientations) is empty by computing the expected root from the specific position and comparing it to the actual `Root`.
In case all assertions pass, the `Root` and `Size` state variables are updated to the new state.
```python
append = Seq([
Assert(Txn.application_args.length() == Int(NUM_APP_ARGS_APPEND)),
Assert(Txn.application_args[VALUE_INDEX] != Bytes('')),
Assert(App.globalGet(Bytes('Root')) == calc_root(
Sha256(Bytes(''))
)),
App.globalPut(Bytes('Root'), calc_root(
Sha256(
Txn.application_args[VALUE_INDEX]
)
)),
App.globalPut(Bytes('Size'), App.globalGet(Bytes('Size')) + Int(1)),
Int(1)
])
```
Note we have the following constants in the code:
- `NUM_APP_ARGS_APPEND` - the number of expected arguments for the **append** operation.
- `VALUE_INDEX` - index of the value in the application arguments array.
#### verify sequence
The **verify** sequence first validates that the correct number of application arguments were received.
It then computes the expected root according to the value and siblings array and compares it to the actual `Root`.
```python
verify = Seq([
Assert(Txn.application_args.length() == Int(NUM_APP_ARGS_VERIFY)),
Assert(App.globalGet(Bytes('Root')) == calc_root(
Sha256(Txn.application_args[VALUE_INDEX])
)),
Int(1)
])
```
`NUM_APP_ARGS_VERIFY` - the number of expected arguments for the **verify** operation.
#### update sequence
The **update** sequence first validates that the correct number of application arguments were received and that the value to update is not an empty byte-slice.
It then computes the expected root according to the value and siblings array and compares it to the actual `Root`.
In case all assertions pass, the `Root` state variables is updated to the new state.
```python
update = Seq([
Assert(Txn.application_args.length() == Int(NUM_APP_ARGS_UPDATE)),
Assert(Txn.application_args[UPDATE_VALUE_INDEX] != Bytes('')),
Assert(App.globalGet(Bytes('Root')) == calc_root(
Sha256(
Txn.application_args[VALUE_INDEX]
)
)),
App.globalPut(Bytes('Root'), calc_root(
Sha256(
Txn.application_args[UPDATE_VALUE_INDEX]
)
)),
Int(1)
])
```
Note we have the following constants in the code:
- `NUM_APP_ARGS_UPDATE` - the number of expected arguments for the **update** operation.
- `VALUE_INDEX` - index of the `old` value in the application arguments array.
- `UPDATE_VALUE_INDEX` - index of the `new` value in the application arguments array.
#### The approval program
The final approval program is simply a router to all the above sequences in addition to allowing `OptIn` to all
and restricting `DeleteApplication` and `UpdateApplication` from anyone other than the application creator.
```python
program = Cond(
[Txn.application_id() == Int(0), on_creation],
[Txn.on_completion() == OnComplete.OptIn, Approve()],
[Txn.on_completion() == OnComplete.DeleteApplication, Return(Txn.sender() == Global.creator_address())],
[Txn.on_completion() == OnComplete.UpdateApplication, Return(Txn.sender() == Global.creator_address())],
[
Txn.on_completion() == OnComplete.NoOp,
Cond(
[Txn.application_args[COMMAND_INDEX] == Bytes('verify'),
Return(verify)],
[Txn.application_args[COMMAND_INDEX] == Bytes('append'),
Return(append)],
[Txn.application_args[COMMAND_INDEX] == Bytes('update'),
Return(update)]
)
]
)
```
### some caveats
Using this smart-contract implementation with large trees might exceed the operational cost limit allowed smart-contracts on the AVM.
Luckily, we can use AVM's pooled opcode budget feature by grouping our original application calls with "Dummy" application calls and thus increasing our operational budget.
For example, we could create the following approval code to use as a "Dummy" application:
```python
def dummy_approval():
return Approve()
```
The above has the minimal operation cost for a TEAL program and thus grouping calls to it with other "expensive" calls will substantially increase our operational budget.