# Modul 2: Core Quantum Physics for Quantum Computing

## Objektif

1. Peserta memahami perbedaan fundamental antara bit klasik dan qubit.
2. Peserta memahami konsep superposisi sebagai kemampuan qubit untuk berada di banyak state sekaligus.
3. Peserta memahami pengukuran (measurement) sebagai proses untuk mendapatkan hasil klasik dari qubit dan sifatnya yang probabilistik.
4. Peserta memahami keterkaitan kuantum (entanglement) sebagai koneksi antar-qubit yang saling memengaruhi.
5. Peserta memahami Bloch Sphere sebagai alat visualisasi untuk satu qubit.
6. Peserta memahami fungsi gerbang kuantum dasar (H, X, Z, CNOT).

## Dasar Teori
### Qubit
Bit klasik hanya dapat berada dalam satu dari dua state, yaitu 0 atau 1. Sebaliknya, qubit dapat berada dalam superposisi dari kedua state tersebut, yang memungkinkan komputasi kuantum memiliki potensi yang jauh lebih besar dibandingkan komputasi klasik. Secara praktis, qubit dapat dicapai dengan berbagai cara, seperti menggunakan spin elektron, polaritas foton, atau tingkat energi atom. Bootcamp ini tidak akan membahas implementasi fisik qubit, tetapi fokus pada konsep dasar dan cara operasi dilakukan pada qubit.

### Superposition
Pada ukuran partikel yang sangat kecil, seperti elektron atau foton, partikel-partikel dapat berada dalam beberapa state sekaligus. Misalnya, sebuah qubit dapat berada dalam state 0 dan 1 secara bersamaan, yang dikenal sebagai superposisi. Ketika qubit di-*measure*, ia akan *collapse* ke salah satu dari dua state tersebut. Ketika dalam keadaan superposisi, qubit dapat direpresentasikan sebagai kombinasi linear dari state 0 dan 1 dengan menggunakan notasi dirac, yaitu:
$$\large |q\rangle = \alpha |0\rangle + \beta |1\rangle$$
di mana $\alpha$ dan $\beta$ adalah koefisien kompleks yang memenuhi kondisi normalisasi:
$$\large |\alpha|^2 + |\beta|^2 = 1$$

Masing-masing $|\alpha|^2$ dan $|\beta|^2$ dapat diartikan sebagai probabilitas mengukur qubit dalam keadaan $|0⟩$ atau $|1⟩$.

State dasar qubit dapat direpresentasikan dalam bentuk vektor kolom sebagai berikut:
$$\large |0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad |1\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$$

State |0⟩ berarti qubit berada dalam state 0 dengan probabilitas 100%, sedangkan state |1⟩ berarti qubit berada dalam state 1 dengan probabilitas 100%. Kombinasi linear dari kedua state ini dapat direpresentasikan sebagai:
$$\large |q\rangle = \alpha \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \beta \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix}$$

Perlu diingat dan ditekankan bahwa ketika dalam superposisi, qubit tidak berada di antara 0 dan 1, tetapi benar-benar berada di kedua state tersebut sekaligus.

### Measurement
Measurement merupakan aspek penting dalam komputasi kuantum karena hasil akhir dari algoritma kuantum harus diubah menjadi informasi klasik yang dapat dipahami dan digunakan. Oleh karena itu, memahami bagaimana measurement bekerja dan bagaimana probabilitasnya dihitung sangat penting bagi siapa saja yang ingin bekerja dengan komputasi kuantum.

Ketika qubit di-*measure*, state superposisinya akan *collapse* menjadi salah satu dari dua state dasar, yaitu |0⟩ atau |1⟩. Proses ini bersifat probabilistik, di mana probabilitas mendapatkan hasil tertentu ditentukan oleh koefisien $\alpha$ dan $\beta$. Secara matematis, probabilitas mengukur qubit dalam state |0⟩ adalah $|\alpha|^2$, sedangkan probabilitas mengukur qubit dalam state |1⟩ adalah $|\beta|^2$. Setelah *measurement*, qubit tidak lagi berada dalam superposisi, melainkan berada dalam state hasil pengukuran tersebut. Qubit yang telah di-*measure* tidak dapat kembali ke state superposisi sebelumnya, kecuali melalui proses kuantum tertentu terlebih dahulu.

Dalam praktisnya, salah satu cara untuk melakukan measurement adalah dengan melakukan measurement dengan frekuensi yang besar. Misalnya, ketika kita memiliki qubit dalam state superposisi dengan probabilitas 70% untuk |0⟩ dan 30% untuk |1⟩, kita dapat melakukan measurement sebanyak 1000 kali. Dari 1000 kali measurement tersebut, kita mungkin mendapatkan mendekati 700 hasil |0⟩ dan 300 hasil |1⟩.

### Entanglement
Sebuah properti unik dari quantum particle lainnya adalah *entanglement*. Ketika dua qubit atau lebih berada dalam keadaan *entangled*, state dari satu qubit tidak lagi dapat dijelaskan secara independen dari state qubit lainnya, bahkan jika mereka dipisahkan oleh jarak yang sangat jauh. Ini berarti bahwa pengukuran pada satu qubit akan langsung memengaruhi state qubit lainnya.

Secara intuitif, kita dapat membayangkan suatu sistem yang terdiri dari dua elektron yang memiliki spin masing-masing. Elektron hanya memiliki dua kemungkinan spin, yaitu +1/2 (up) atau -1/2 (down). Jika kita tahu bahwa total spin dari sistem tersebut adalah nol, maka ketika kita mengukur spin dari salah satu elektron dan menemukan bahwa spinnya adalah "up", kita secara otomatis tahu bahwa spin dari elektron lainnya pasti "down", tanpa perlu mengukurnya secara langsung. Akan tetapi, sebelum measurement dilakukan, kedua elektron tersebut berada dalam superposisi dari kedua kemungkinan spin tersebut. Ini adalah contoh sederhana dari *entanglement*. Measurement suatu qubit akan langsung memengaruhi state qubit lainnya, terlepas dari jarak fisik di antara mereka.
### Bloch Sphere
Untuk memvisualisasikan state dari satu qubit, kita dapat menggunakan representasi geometris yang disebut Bloch Sphere. Bloch Sphere adalah sebuah bola tiga dimensi di mana setiap titik pada permukaan bola tersebut merepresentasikan state superposisi dari qubit. Pada Bloch Sphere, state |0⟩ direpresentasikan oleh titik di kutub utara, sedangkan state |1⟩ direpresentasikan oleh titik di kutub selatan. Setiap state superposisi lainnya dapat direpresentasikan oleh titik-titik di antara kedua kutub tersebut. Berikut adalah ilustrasi dari Bloch Sphere:


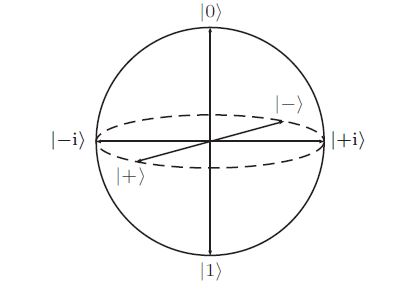
Seperti yang dapat kita lihat, bloch sphere memiliki tiga sumbu utama, yaitu sumbu X, Y, dan Z. Setiap state qubit dapat direpresentasikan sebagai vektor yang berasal dari pusat bola menuju permukaan bola. Vektor ini dapat dinyatakan dalam koordinat bola dengan dua sudut, yaitu θ (theta) dan φ (phi). Sudut θ mengukur jarak dari kutub utara (state |0⟩) ke titik pada permukaan bola, sedangkan sudut φ mengukur rotasi di sekitar sumbu Z.

### Quantum Gates
Mirip dengan logika gerbang pada komputasi klasik, komputasi kuantum juga memiliki gerbang kuantum (quantum gates) yang berfungsi untuk memanipulasi state dari qubit. Quantum gates adalah operasi matematis yang diterapkan pada qubit untuk mengubah state-nya. Beberapa contoh quantum gates yang umum digunakan antara lain:
- **Pauli-X Gate (NOT Gate)**: Berfungsi sebagai NOT gate pada komputasi klasik, yang membalik state |0⟩ menjadi |1⟩ dan sebaliknya.
- **Hadamard Gate (H Gate)**: Mengubah state dasar |0⟩ menjadi superposisi (|0⟩ + |1⟩)/√2 dan |1⟩ menjadi (|0⟩ - |1⟩)/√2.
- **CNOT Gate (Controlled-NOT Gate)**: Gerbang ini memiliki dua qubit sebagai input. Jika qubit kontrol (qubit pertama) berada dalam state |1⟩, maka qubit target (qubit kedua) akan dibalik (|0⟩ menjadi |1⟩ dan sebaliknya). Jika qubit kontrol berada dalam state |0⟩, maka qubit target tidak berubah.
- **Toffoli Gate (CCNOT Gate)**: Gerbang ini memiliki tiga qubit sebagai input. Jika kedua qubit kontrol (qubit pertama dan kedua) berada dalam state |1⟩, maka qubit target (qubit ketiga) akan dibalik. Jika salah satu atau kedua qubit kontrol berada dalam state |0⟩, maka qubit target tidak berubah.
- **Rotational Gate (RX, RY, RZ)**: Gerbang ini berfungsi untuk memutar state qubit di sekitar sumbu X, Y, atau Z pada Bloch Sphere. Rotational gate dapat digunakan untuk mengubah fase dan amplitudo dari state qubit.
- **U Gate**: Gerbang ini adalah gerbang kuantum universal yang dapat digunakan untuk merepresentasikan semua operasi kuantum pada satu qubit. U gate dapat dikonfigurasi dengan tiga parameter sudut (θ, φ, λ) untuk menghasilkan berbagai transformasi pada state qubit.
- **SWAP Gate**: Gerbang ini berfungsi untuk menukar state antara dua qubit. Jika qubit A berada dalam state |0⟩ dan qubit B berada dalam state |1⟩, setelah melalui SWAP gate, qubit A akan berada dalam state |1⟩ dan qubit B akan berada dalam state |0⟩.
- **Phase Gates (S, T)**: Gerbang ini menambahkan fase tertentu pada state |1⟩ tanpa mengubah state |0⟩. Misalnya, S gate menambahkan fase π/2 (90 derajat) pada state |1⟩, sedangkan T gate menambahkan fase π/4 (45 derajat).

### Quantum Circuits
Pada quantum computing, quantum circuits adalah serangkaian operasi kuantum yang diterapkan pada qubit untuk melakukan komputasi. Rangkaian kuantum terdiri dari qubit sebagai input, quantum gates sebagai operasi, dan hasil akhir yang diperoleh setelah measurement. Rangkaian kuantum dapat direpresentasikan secara grafis menggunakan diagram sirkuit, di mana qubit digambarkan sebagai garis horizontal dan quantum gates digambarkan sebagai simbol-simbol yang ditempatkan di sepanjang garis tersebut. Berikut adalah contoh sederhana dari rangkaian kuantum:
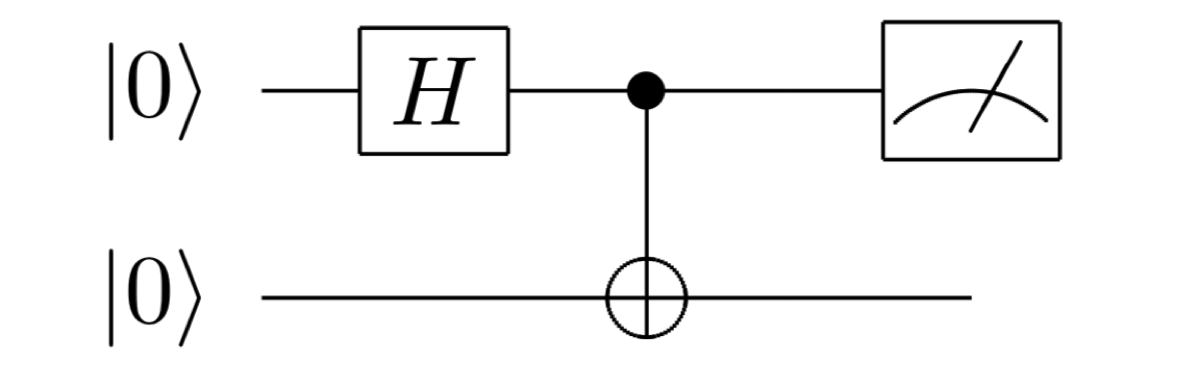
Pada contoh di atas, kita memiliki dua qubit sebagai input. Qubit diinisialisasi dalam state |0⟩. Kemudian, qubit pertama melewati Hadamard gate (H), yang mengubahnya menjadi superposisi. Setelah itu, kedua qubit melewati CNOT gate, di mana qubit pertama berfungsi sebagai control qubit dan qubit kedua sebagai target qubit. Akhirnya, qubit di-*measure* untuk mendapatkan hasil klasik (0 atau 1).

Quantum circuits dapat digunakan untuk mengimplementasikan berbagai algoritma kuantum. Dalam praktis sebenarnya, sebuah quantum circuit tidak mewakili rangkaian fisik di dunia nyata, tetapi hanya sebagai representasi dari operasi kuantum yang dilakukan pada qubit dalam urutan waktu. Quantum circuit dapat dioptimalkan untuk mengurangi jumlah quantum gates yang digunakan, sehingga meningkatkan efisiensi. Dengan memahami konsep dasar qubit, superposisi, measurement, entanglement, dan quantum gates, kita dapat mulai merancang dan menganalisis quantum circuit untuk berbagai implementasi.