# Modul 3: Bulding Blocks of Transformer: Attention Mechanism and MLP
## Objektif
Setelah menyelesaikan modul ini, peserta diharapkan dapat:
1. Memahami input dan output softmax function
2. Memahami intuisi dari self-attention mechanism pada Transformer
3. Memahami konsep matriks Query, Key, dan Value untuk membentuk attention pada Transformer
4. Memahami cara mengolah input menjadi matriks Query, Key, dan Value dengan python
5. Memahami konsep transformasi linear dan non-linear pada MLP
6. Memahami cara mengolah output attention logits dengan MLP

## Dasar Teori
### 1. Pendahuluan
Pada modul sebelumnya, kita telah melihat arsitektur Transformer secara garis besar, yang terdiri dari tumpukan Encoder dan Decoder. Kita juga telah belajar bahwa setiap blok penyusunnya memiliki dua komponen inti: sebuah lapisan Self-Attention dan sebuah lapisan Feed-Forward Neural Network (FFN). Namun, sebelum sebuah kalimat bisa diproses oleh Transformer, kalimat tersebut harus diubah terlebih dahulu ke dalam format yang bisa dipahami oleh komputer: angka.


Tokenization digunakan untuk memecah kalimat menjadi unit kecil token yang memiliki id unik. Kemudian setiap token ini akan diubah menjadi word embedding merepresentasikan makna dari token tersebut dalam sebuah ruang multi-dimensi. Kumpulan vektor embedding dari sebuah kalimat inilah yang menjadi input sesungguhnya bagi lapisan pertama Transformer, yaitu Self Attention.

### 2. Intuisi Self-Attention
Self-Attention adalah otak utama dari Transformer, ini adalah perbedaan utama antara Transformer dengan model sekuensial sebelumnya seperti RNN dan LSTM. Self-Attention menjadi solusi dari permasalahan menghubungkan sebuah kata dengan kata lain yang posisinya sangat jauh di dalam kalimat, yang dikenal sebagai masalah konteks jangka panjang. Contohnya dalam masalah ambiguitas:

1. The animal didn't cross the street because it was too tired.
2. The animal didn't cross the street because it was too wide.

Bagi manusia, perbedaannya jelas, dimana pada kalimat pertama kata ganti "it" merujuk ke "animal". Namun, pada kalimat kedua kata ganti "it" merujuk ke "street". Dimana, makna kata "it" ini bergantung pada **Konteks**. Sebuah mesin bisa mengerti permasalahan akibat perbedaan ini berkat Self-Attention. Alih-alih memproses kata satu per satu, mekanisme self-attention memungkinkan setiap kata dalam sebuah kalimat untuk "melihat" semua kata lain di kalimat yang sama secara bersamaan (Paralel).

### 3. Mekanisme Attention: Query, Key, dan Value
Cara dari transformer untuk "melihat" dan "menimbang" untuk mendapatkan konteks adalah dengan menggunakan 3 vektor khusus: Query, Key, dan Value.


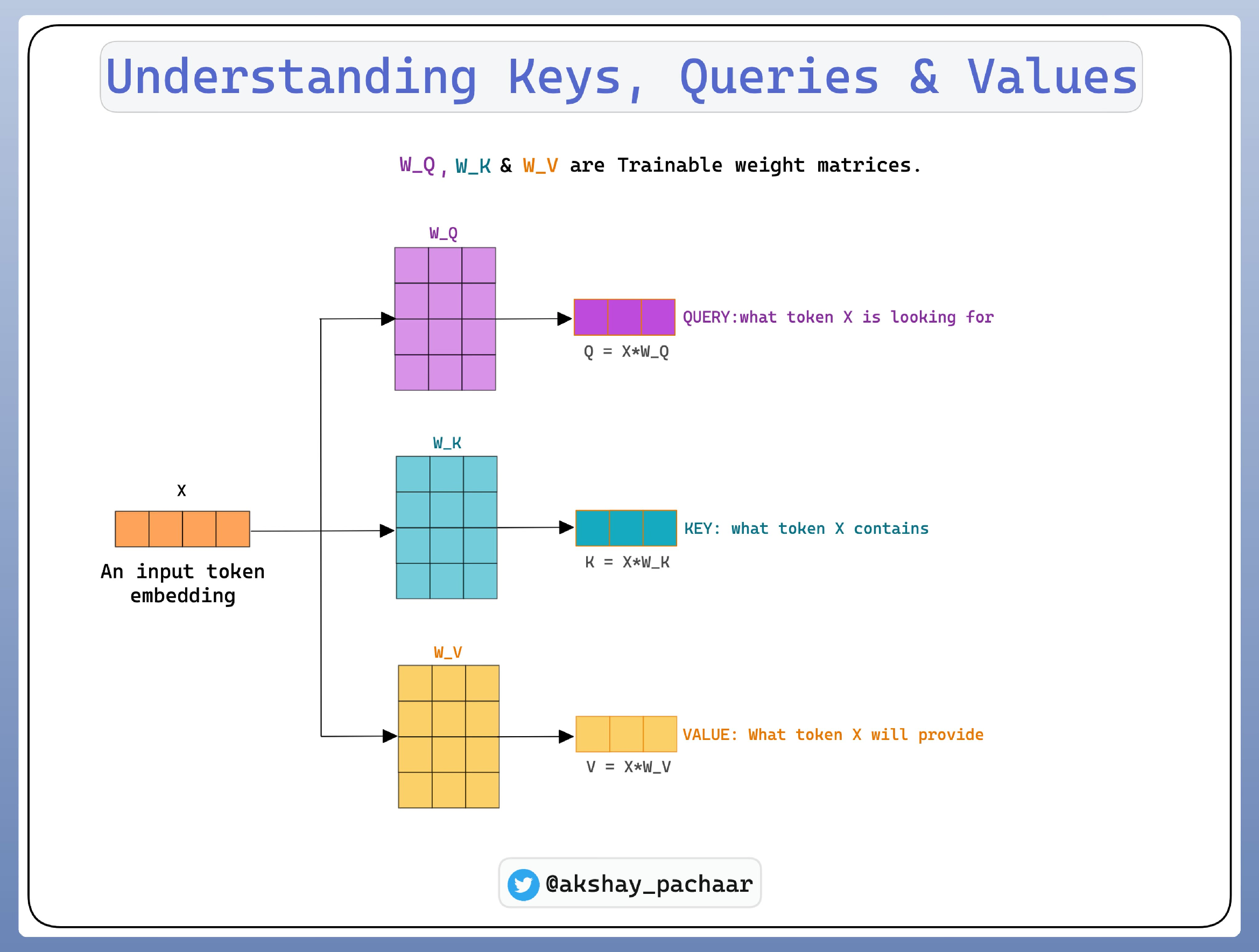
1. Query (Q): Vektor yang merepresentasikan kata saat ini yang sedang aktif mencari konteks. Ia adalah "pertanyaan" yang diajukan oleh kata tersebut.
2. Key (K): Vektor yang berfungsi sebagai "label" atau "kunci" dari sebuah kata. Ia menawarkan diri untuk dicocokkan dengan sebuah Query.
3. Value (V): Vektor yang berisi makna atau informasi sesungguhnya dari sebuah kata. Vektor inilah yang akan diambil jika Key-nya cocok dengan Query.

### 4. Langkah-langkah Perhitungan Self-Attention
1. Membuat Matriks Q, K, dan V

Vektor Embedding yang sudah didapatkan tidak langsung digunakan, tetapi dibuat 3 proyeksi linear yang berbeda untuk setiap kata. Caranya adalah mengalikan matriks input embeddings (X) dengan tiga matriks bobot berbeda (Wq, Wk, Wv) yang dipelajari selama proses training.

$$Q = X \cdot W^Q$$
$$K = X \cdot W^K$$
$$V = X \cdot W^V$$

2. Menghitung Skor (Score)

Untuk menentukan seberapa relevan setiap kata lain terhadap sebuah kata yang sedang diproses, maka diperlukan skor. Skor ini didapatkan dengan melakukan operasi perkalian titik (dot product) antara vektor Query dari kata saat ini dengan vektor Key dari setiap kata lain dalam kalimat (termasuk dirinya sendiri). Semakin besar skornya, maka menandakan relevansi yang semakin kuat.


3. Pembagian & Normalisasi (Scaling)

Dot product dapat menghasilkan nilai yang sangat besar, yang dapat menyebabkan masalah saat training. Untuk menstabilkan ini, para peneliti membagi skor dengan akar kuadrat dari dimensi dari Key Vektor ($d_k$) untuk memastikan bahwa nilai-nilai skor tetap berada dalam rentang yang wajar.

4. Fungsi Softmax

Angka yang dinormalisasi tadi masih dalam angka mentah (logits). Sehingga, masih perlu diubah dalam distribusi probabilitas yang merupakan nilai antara 0 dan 1, di mana total jumlahnya adalah 1. Oleh karena itu, digunakan lah fungsi **Softmax** untuk didapatkan **Attention Weight**.

5. Menghasilkan Output

Output didapatkan dari mengalikan Attention Weight dengan vektor value (V) dari setiap kata, lalu menjumlahkannya. Hasilnya adalah sebuah vektor baru yang telah diperkaya dengan informasi kontekstual dari kata-kata paling relevan di seluruh kalimat.


Contoh kode yang dapat dicoba di python:

import numpy as np

np.set_printoptions(precision=3, suppress=True)
rng = np.random.default_rng(0)

# 1) Input embeddings: 3 token, dim=4 
X = np.array([
    [1.0, 0.0, 0.0, 0.1],  # token-1
    [0.0, 1.0, 0.0, 0.1],  # token-2
    [0.0, 0.0, 1.0, 0.1],  # token-3
], dtype=float)                    # shape: (L=3, d_model=4)

# 2) Inisialisasi Wq, Wk, Wv (di model asli: parameter terlatih)
#    Di sini pakai angka acak yang tetap (seeded) supaya reproducible.
d_model = X.shape[1]
Wq = rng.normal(0, 0.5, size=(d_model, d_model))
Wk = rng.normal(0, 0.5, size=(d_model, d_model))
Wv = rng.normal(0, 0.5, size=(d_model, d_model))

# 3) Q, K, V = X @ W
Q = X @ Wq   # (L, d_model)
K = X @ Wk   # (L, d_model)
V = X @ Wv   # (L, d_model)

print("X (embeddings):\n", X, "\n")
print("Q:\n", Q, "\n")
print("K:\n", K, "\n")
print("V:\n", V, "\n")

# 4) Attention logits = QK^T / sqrt(d_k)
dk = Q.shape[1]
scores = (Q @ K.T) / np.sqrt(dk)  # (L, L)
print("Attention logits (QK^T / sqrt(dk)):\n", scores, "\n")

# 5) Softmax row-wise → attention weights (tiap baris jumlahnya = 1)
def softmax(a, axis=-1):
    a = a - np.max(a, axis=axis, keepdims=True)  # stabilitas numerik
    e = np.exp(a)
    return e / e.sum(axis=axis, keepdims=True)

weights = softmax(scores, axis=-1)  # (L, L)
print("Attention weights (softmax per baris):\n", weights, "\n")

# 6) Weighted sum atas V → context vectors
context = weights @ V  # (L, d_model)
print("Context vectors (weights @ V):\n", context, "\n")

# Token yang paling diperhatikan tiap baris
for i in range(weights.shape[0]):
    j = int(np.argmax(weights[i]))
    print(f"Token {i} paling fokus ke token {j} (bobot={weights[i,j]:.3f})")

### 5. FFN dalam Transformer

Setelah mendapatkan vektor output yang kaya makna pada lapisan self-attention, vektor ini perlu diproses lebih lanjut agar model dapat "memikirkan" dan "memahami" informasi tersebut secara lebih mendalam. Inilah fungsi dari Feed-Forward Network (FFN). Jika self-attention adalah tentang mengumpulkan informasi dari tetangga, maka FFN adalah tentang memproses informasi itu secara individual. Tujuan utamanya adalah untuk menambah kapasitas model dengan lebih banyak parameter yang dapat dipelajari, sehingga dapat meningkatkan kemampuan untuk memahami pola yang kompleks. Dalam FFN ini juga diterapkan metode Non-Linearitas. Non-Linearitas inilah yang membantu model untuk belajar hubungan yang jauh lebih rumit daripada sekadar kombinasi linear, sehingga model dapat belajar pola yang rumit dan melengkung, seperti hubungan kompleks dalam bahasa. Input dari FFN ini merupakan output dari lapisan self-attention.

### 6. Arsitektur FFN: Transformasi Linear dan Non-Linear

FFN memiliki bentuk arsitektur yang terdiri dari 2 lapisan linear yang dipisahkan oleh sebuah fungsi aktivasi non-linear. Proses didalamnya terjadi dalam 3 langkah:
1. Lapisan Linear Pertama (Ekspansi)

Lapisan ini adalah transformasi linear, dimana akan mengambil vektor input dan memperbesar dimensinya. Dalam paper 'Attention All You Need' dimensi input 512 diperbesar menjadi 2048. Tujuannya adalah untuk memberi model lebih banyak ruang kerja untuk memisahkan dan mempelajari hubungan antar fitur yang kompleks.

2. Fungsi Aktivasi Non-Linear

Lapisan ini adalah transformasi non-linear, dimana setelah diekspansi, hasilnya akan dilewatkan ke fungsi aktivasi (ReLU/GeLU/dll).


Ini adalah langkah yang memungkinkan model mempelajari pola yang rumit. Tanpa "patahan" yang diciptakan oleh fungsi aktivasi, seluruh FFN hanya akan menjadi satu operasi linear besar, yang sangat membatasi kemampuan belajar model.

3. Lapisan Linear Kedua (Proyeksi Kembali)

Lapisan ini adalah transformasi linear kembali, dimana output dari fungsi aktivasi akan diproyeksikan kembali ke dimensi semula. Tujuanny adalah untuk mengubah vektor ke dimensi yang sesuai agar bisa menjadi input untuk blok Transformer berikutnya.