[TOC]

---

# Part 1 簡介 Introduction

## 1.1 統計基本概念與專有名詞
1. **統計學(Statistics)** : 統計學為**蒐集、整理、展示、分析、解釋**資料，並由樣本推論群體，使在不確定的情況下做成決策的科學方法。
2. **群體(population)** : 由具有**共同特性**之個體所組成的整體。
3. **樣本(sample)** : **群體**之一部分。
4. **參數(parameter)** : 由**群體**資料所計算之群體**表徵值**。
5. **統計量(statistic)**: 由**樣本**資料所計算之樣本**表徵值**。
6. **統計學的主要目的(The objective of Statistics)** : 由**樣本**所得之資訊來推論**母體參數**。
7. **統計學的範圍** : 統計學可分為**敘述統計(Descriptive Statistics)** 及**推論統計(Inferential Statistics)** :
<br>
 <br>
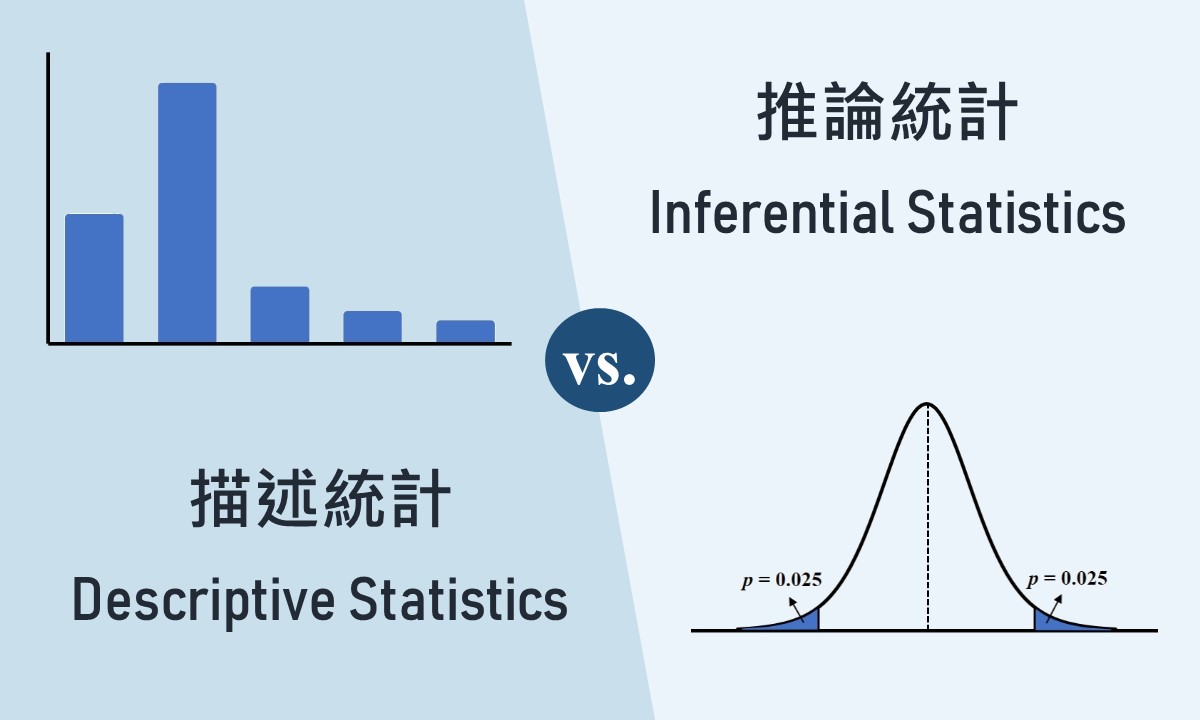<br><br>

8. **進行統計分析之五大步驟** :
- Step 1 : 定義欲研究之問題及與該問題相關之群體。
- Step 2 : 規劃實驗或問卷。
- Step 3 : 收集及分析資料。
- Step 4 : 進行統計推論。
- Step 5 : 衡量統計推論之可靠度。

9. **隨機變數(Random Variable, R.V.)** : 研究者對所欲研究問題定義之群體所或感興趣的一項或多項特質，稱為**隨機變數**。觀察各項隨機變數之結果稱為資料(data)。

**隨機變數之類別(Types of Variables)** :
- **定性**變數(**Qualitative** random variables) : 定性變數產生**類別**資料，即隨機變數的各結果**不能以數量**表示，而僅能依其特性之**類別**表之。
例如 : 性別、國籍、造成產品變異之可能原因
- **定量**變數(**Quantitative** random variables) : 定量變數產生**數值**資料，即隨機變數的各結果**可以數量**表之。
- **離散型**資料(**Discrete** Random variables) : 經由**計數**的方式取得變數之資料。例如 : 不良品個數、一份文件的錯字數、晶圓上的缺陷點數
> 離散型變數之可能值 : 0 或正整數。
- **連續型**變數(**Continuous** data) : 經由**量測**的方式取得變數資料。例如 : 重量、高度
> 連續型變數之可能值 : 任何實數。
> 定量隨機變數通常以大寫英文字母$X$或$Y$表示。

10. **實驗單位(Experimental Unit)** : 研究者由所欲研究之**人或物**上取得**隨機變數**之**量測值，這些人或物**稱為**實驗單位**。

### 參數
- 群體平均數 : M (mu)
- 群體標準差 : $\sigma$ (sigma)
- 群體比例 : P，代表群體(population)
- 樣本統計量 : $\bar{x}$ (x-bar)
- 樣本標準差 : s
- 樣本比例 : $\hat{p}$

## 1.2 常用統計圖表

資料蒐集後，可依**隨機變數**類別建立統計表格(Statistical table)，再利用此表格繪製統計圖，已取得以下資訊 :
- **隨機變數之**資料分佈(data distribution)
- **隨機變數之**那些數據出現最多次或最少次

### 1.2.1 Graphs for Categorical Data
條圖(Bar Graph)、單圓圖(Pie Chart)與柏拉圖(Pareto Diagram)通常用來表示**類別變數**(**定性**資料)之資料分佈。

**條圖** : 主要用來比較及對照不同類別或時期間的差異。
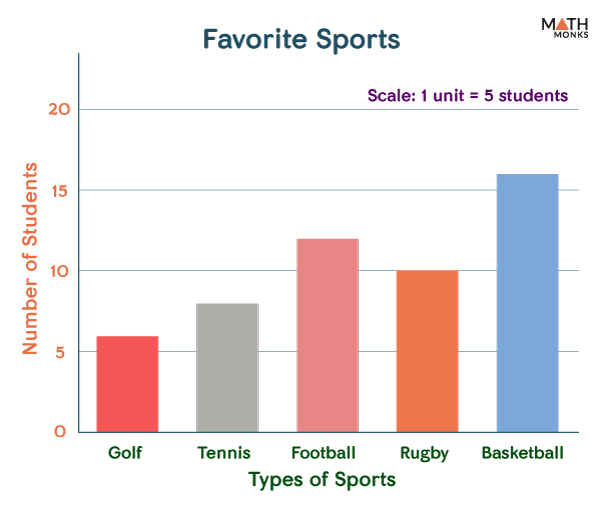<br><br>

**單圓圖** : 主要用來顯示一個**單一總和量**如何攤分於各種類別中。

<br><br>

- **柏拉圖** : 工業界最常使用之**定性**(類別型)資料圖形。可以依據柏拉圖提出之「**重要少數，瑣細多數**」理論，找出造成問題最關鍵之少數因素，以進行改善。
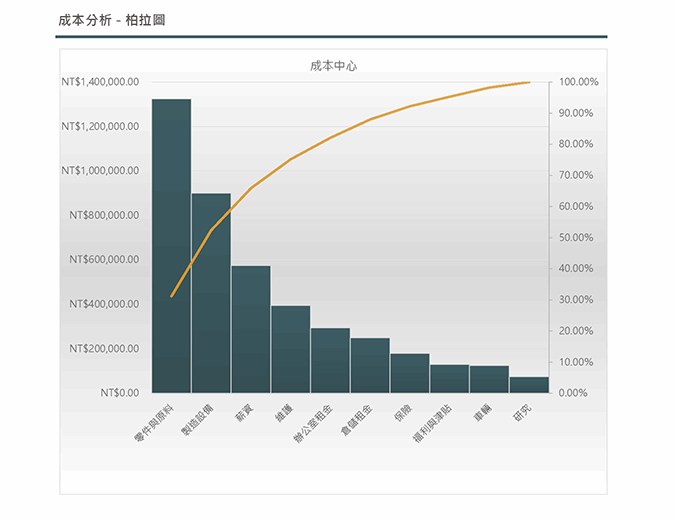<br>
> 每一條中間不能有空隙，且必須經過排列，由高到低。

### 1.2.2 定量型資料常用之圖表
莖葉圖(Stem-and-Leaf Display)、直方圖(Histogram)、散佈圖(Scatter Diagram)與時間序列圖(Line Chart)常用來表**數值變數**(**定量**資料)。

- **莖葉圖** : 每筆資料由莖(前頭的數字)與葉(最後一個數字)所快速組成。<br>
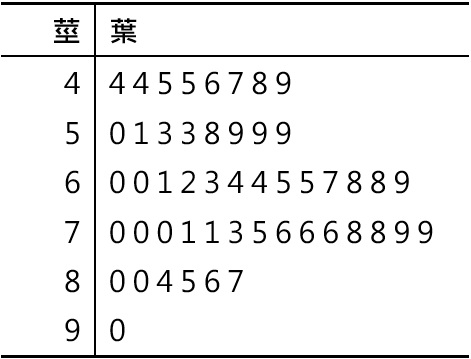<br><br>

- **直方圖** : **連續型**資料最常使用的圖形，用來展示**資料之分佈**。<br>
<br>

- **散佈圖** : **散佈圖**主要用來表示資料**兩個變數**間的關係。
<br>

- **時間序列圖** : **時間序列圖(line chart)**是用來表示資料在不同**時間**的**關係圖**，通常**時間**為**橫軸**，而**縱軸**則表示**觀測值的單位數量**。<br>
<br>

## 1.3 數據取得方式

1. **普查** : 在欲研究之群體中蒐集每一個體之資料，也就是100%的全檢。
2. **抽查(Sampling)** : 利用一種程序或方法，由群體中抽出樣本。常用的**抽樣方法**有下列四種 :
- 簡單隨機抽樣
- 系統抽樣
- 分層隨機抽樣
- 部落抽樣

### 1.3.1 簡單隨機抽樣
指群體中每一個體被抽種之機會均相同。
作法 : 對群體內的每個個體編號，再以亂數表、電腦模擬亂數或製作紙籤的方法決定欲抽取之樣本。
**優點** : 取樣方法簡便。
**缺點** : 有時會因抽到的樣本過於集中在某部分之群體，而造成樣本之**代表性不足**。

### 1.3.2 系統抽樣
只做第一次隨機抽樣，然後依固定間隔數抽出一樣本，直至抽出所欲知樣本數。
**優點** : 抽出第一個種子號碼後，僅需每間隔數個樣本抽樣即可，取樣方法簡便。
**缺點** : 樣本在**編號排序**時，必須與研究者所關心的變數**無關**，否則會造成樣本之**代表性不足**。

### 1.3.3 分層隨機抽樣
作法 : 先將群體依某依衡量標準分成數個不重疊的子群(稱為層)，再從每一子群(層)中利用簡單隨機方式抽取樣本。
分層隨機抽樣之原則是同層內的性質差異要小，而不同層間之差異則要越大越好。

### 1.3.4 部落抽樣
常用在群體中之個體分離相當遠，且很難蒐集到其樣本資料時。
作法 : **部落抽樣**先將群體分成數個**部落**，再從同一個部落中抽出一個或數個部落進行**普查**。
**部落抽樣**是假設每一個部落都是**群體**的縮影，因此不同部落間個體性質的差異要小，而同一部落內個體性質的差異性大。

<br>

---

# Part 2 利用指標來描述資料 Describing Data with Numerical Measures

## 2.1 如何以數值指標來描述資料

**連續型資料有以下四個特性:**
1. **集中趨勢(Central Tendency)(or Location)**
2. **分散或變異趨勢(Dispersion or Variability)**
3. **偏態(Skewness)**
4. **峰度(Kurtosis)**
<br>

### 2.1.1 集中趨勢
指資料有往資料之**中央位置**靠近的趨勢。「**集中趨勢**指標」是表示一組數據**中央點**位置所在的一個**指標**。
常用的**集中趨勢指標** : <b> 平均數(mean)、中位數(median)、眾數(mode)。 </b>

1. 平均數 : <br>
群體平均數 : $\mu = \frac{\sum X_i}{N}$ <br>
樣本平均數 : $\bar{X} = \frac{\sum X_i}{n}$ <br>
其中$N$表群體大小，$n$表樣本大小。$\bar{X}$ 是 $\hat{M}$(M的估計值)的一種。

2. 中位數 : 將一組數據由小至大排序後，**最中間**的那一個數值稱為**中位數**。
**群體**中位數 : $\eta$ (eta)
**樣本**中位數 : $\tilde x$ (x-tilde)

找中位數之方法 :
- 當 n = 奇數，$\tilde x$ = 排序第 $\frac{(n+1)}{2}$ 位之數值。
- 當 n = 偶數，$\tilde x$ = 排序第 $\frac{n}{2}$ 位及第 $\frac{n}{2}+1$ 位的兩數值之**平均數**。

3. 眾數 : 在一組數據，出現次數**最多**的數值。

**何時用平均數? 何時用中位數或眾數?**
**平均數**對**離群值**非常**敏感**，而**中位數**或**眾數**則對**離群值**較**不敏感**。因此當資料中有**離群值**時，則使用**中位數或眾數**，反之使用**平均數**。
<br>

### 2.1.2 分散 (Dispersion) 或變異 (Variability) 趨勢
「**分散趨勢指標**」是表示一組數據**差異大小**或**數值變化**的一個**量數**。
常用來量測**分散趨勢**的指標 : <b> 全距(Range)、變異數(Variance)、標準差(Standard Deviation)及變異係數(Coefficient of Variation, CV) </b>

1. **全距$(R)$** : **全距**是用來衡量一組數據**分散程度**最簡單的方法。
公式 : R = 最大值 - 最小值<br>
**全距之缺點** :
當一組數據中有**離群值**出現或資料**筆數太多(n>10)**時，全距並非一個很好衡量數距分散程度的量數，因其無法解釋最小值與最大值之間數距分佈的情形。

2. **變異數和標準差**
<b>
群體變異數 : $\sigma^2 = \frac{\sum^N_{i=1}(X_i-\mu)^2}{N}$ <br>
樣本變異數 : $S^2 = \frac{\sum^N_{i=1}(X_i-\bar X)^2}{n-1}$ = $\frac{\sum^N_{i=1}X^2_i-\frac{(\sum X_i)^2}{n}}{n-1}$ = $\frac{平方和-\frac{和的平方}{數據總數}}{數據總數-1}$<br>
群體標準差 : $\sigma = \sqrt{\sigma^2}$<br>
樣本標準差 : $S = \sqrt{S^2}$<br>
</b>
如何用**全距**來估計**標準差**?<br>
**群體標準差 : $\sigma = \frac{R_{population}}{4}$** ; **樣本標準差 : $S = \frac{{R_sample}}{4}$**

3. **變異係數(CV)**
**標準差**和**變異數**是衡量一組數據**絕對**變異(absolute variation)的指標，此指標之大小與數距的**單位尺度**有關，因此若要比較數組單位尺度不同的數據時，需使用一個衡量**相對變異**的指標，即**變異係數**。<br>
變異係數是一個綜合**標準差**跟**平均數**的指標，用來衡量數組資料的**相對分散程度**。$CV$指標是以一組數據之標準差佔其平均數的百分比，是一個**無單位**的指標。<br>
群體相對變異 : $CV = \frac{\sigma}{\mu} * 100\%$<br>
樣本相對變異 : $CV = \frac{S}{\bar x} * 100\%$
<br>

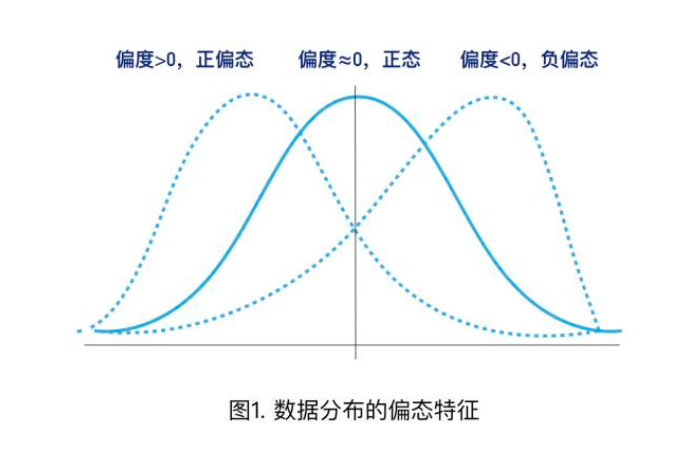
### 2.1.3 偏態(Skewness)
說明一組**數據分佈的型態**(shape of a distribution)。

**單峰**分佈有三種型態 :
1. **對稱(symmetric) : 平均數 = 中位數 = 眾數**
2. **右偏或正偏(right skewness or positive skewness) : 平均數 >> 中位數**
3. **左偏或負偏(left skewness or negative skewness) : 平均數 << 中位數**

#### 偏態係數(Skewness Coefficient, $g_1$) :
- 樣本偏態係數 : $g_1 = \frac{\frac{\sum^n_{i=1}(X_i-\bar{X})^3}{(n-1)}}{S^3}$<br>

偏態係數 = **0** 表示樣本分佈**對稱(symmetric)**
偏態係數 = **+** 表示偏態分佈**偏右(right-skewed)**
偏態係數 = **-** 表示樣本分佈**偏左(left-skewed)**

<br>
<br>

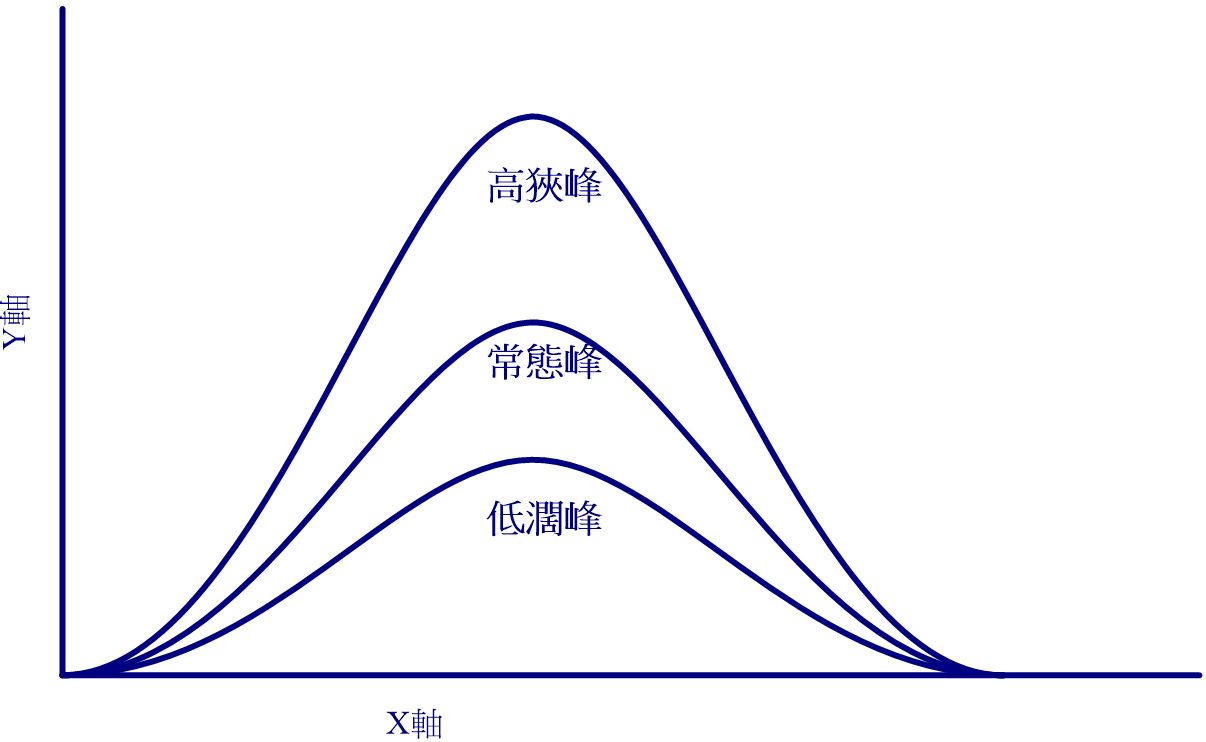
### 2.1.4 峰度(Kurtosis)
- 樣本**峰度係數** : $g_2 = \frac{\frac{\sum^n_{i=1}(X_i-\bar{X})^4}{(n-1)}}{S^4} - 3$<br>

峰度係數 = 0 表示分佈呈**常態峰**
峰度係數 < 0 表示分佈呈**低闊峰**
峰度係數 > 0 表示分佈呈**高狹峰**

<br>
<br>

### 2.1.5 非中趨勢指標(Measures of Non-central Tendency)
1. **百分位(Percentiles)**
**第 p 百分位數**代表在數據資料中有p x 100%的資料**小於或等於**此**第 p 百分位數**。

2. **四分位數(Quartiles)**
第一四分位數$Q_1$ (The first quartile)、第二四分位數$Q_2$ (The second quartile)、第三四分位數$Q_3$ (The third quartile)。

**如何找個四分位數?**
先將資料**排序**，計算$Q_1$的位置 $= 0.25(n+1)$ ; $Q_3 的位置 = 0.75(n+1)$。如$Q_1或Q_3$位置點不是整數，則估算其所在兩位置點間的距離。
<br>

### 2.1.6 衡量分散趨勢的另一個指標(Another Measure of Variability)
1. **中四分位距(Interquartile Range, IQR) : 可避免極端值(extreme values)或離群值(outlier)對全距(Range)在衡量數距變異程度準確性的影響。**
公式 : $IQR = Q_3 - Q_1$
<br>

## 2.2 數據的應用
如何利用**集中趨勢、分散趨勢**及**其他指標**決定**數據之分佈?**
1. **利用經驗法則(The Empirical Rule)**
2. **利用柴比雪夫法則(The Chebyshev's Rule)**
3. **利用盒鬚圖(Box-Whisker Plot)**
4. **利用$Z$分數(Z-Score)**
<br>

### 2.2.1 經驗法則 (The Empirical Rule)
又稱<b>68%-95%-99.73%</b>法則。
> 此法則只適用於**連續型**資料，且資料呈**鐘型**分佈。

- 若數據呈**鐘型**分佈，則約有
68.26% 的數據在 $\mu \pm \sigma$ 範圍內
95.44% 的數據在 $\mu \pm 2\sigma$ 範圍內
99.73% 的數據在 $\mu \pm 3\sigma$ 範圍內
- **如何利用經驗法則找出離群值?**
若有數距落在 **$\mu \pm 3\sigma$ 範圍外**，則該筆數據稱為**離群值(Outlier)**。
<br>

### 2.2.2 利用柴比雪夫法則 (The Chebyshev's Rule)
不論數據呈何種分佈，**至少有$(1-\frac{1}{K^2}) * 100\%$** 的數值會落在 **$\mu \pm K\sigma$ 範圍內
> 此法則只適用於**連續型**資料，資料可為**任何分佈**
<br>

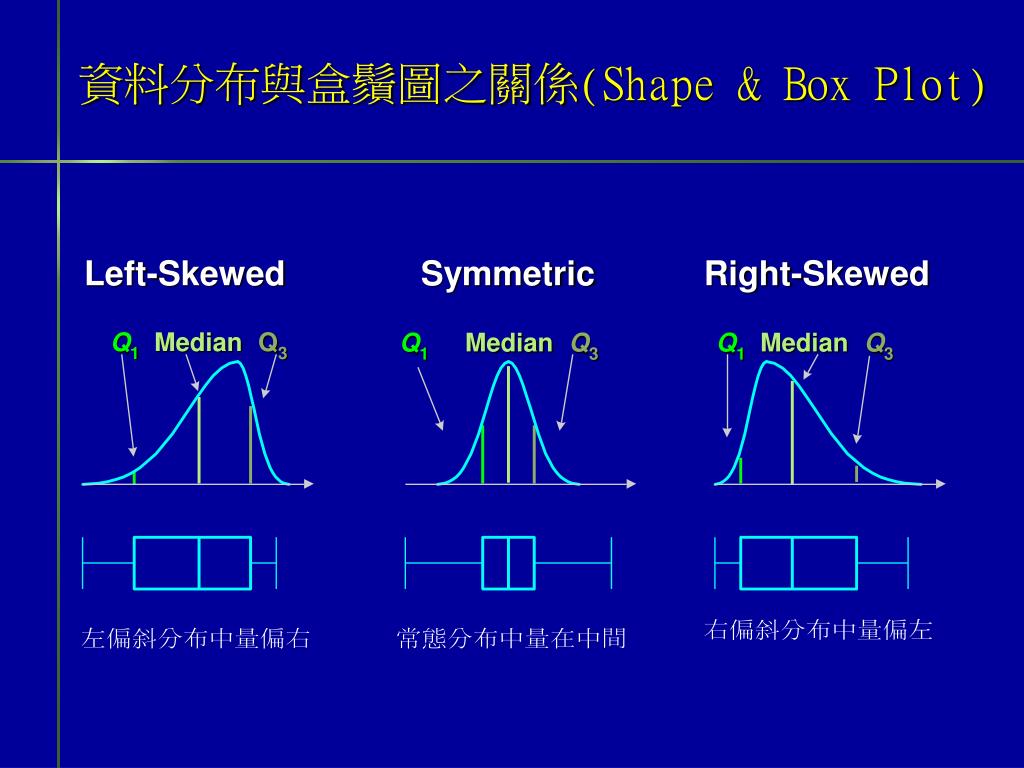
### 2.2.3 盒鬚圖(Box-and-Whisker Plot, Box plot)
**盒鬚圖**是**資料分佈**的一種圖形。可以同時標出資料的**集中趨勢、離中趨勢、偏態、最小值、最大值**等(稱**five-number-summery plot**)，適用於**任何資料分佈**，無論資料為**連續**型或**離散**型。

<br>

- **盒鬚圖主要功用** :
從**視覺上**可有效判斷**資料分佈**及找出資料主要**表徵值**。
- **盒鬚圖其他功用** :

1. **可同時比較數組資料**
2. **可辨認出離群值**
- 超過盒鬚圖之盒 **$1.5 (Q_3-Q_1) 至 3 (Q_3-Q_1)$ 距離內**之值可當作**可能之離群值**。
- 超過盒鬚圖之盒 **$3 (Q_3-Q_1)$ 距離外**之值可當作**非常可能之離群值**。
- **$(Q_3-Q_1) = IQR$**

即一組資料**正常值**的範圍為 **$(Q_1-1.5IQR, Q_3+1.5IQR)$**，此判斷法又稱**中四分位距法**。
<br>

### 2.2.4 Z分數 (Z-score)
Z-score 是一個**標準化**數值，代表**原始數據$(x_i)$偏離其平均數$(\mu)$Z**個**標準差**。<br>

公式 : **$Z_i = \frac{(x_i-\mu)}{\sigma}$**

若 Z-score > 0 代表原始數 $X_i$ **大於**其平均值
若 Z-score < 0 代表原始數 $X_i$ **小於**其平均值
若 Z-score < 0 代表原始數 $X_i$ **等於**其平均值
<br>

## 2.3 加權平均

加權平均數 :
- 群體加權平均數 : $\mu_W = \frac{\sum W_iX_i}{\sum W_i}$, $i = 1, ..., N$<br>
- 樣本加權平均數 : $\bar{X_W} = \frac{\sum W_iX_i}{\sum W_i}$, $i = 1, ..., n$<br>

其$N$表**群體大小**，$n$表**樣本大小**
<br>

---

# Ch3 利用指標來描述雙變量資料 Describing Bivariate Data

## 3.1 什麼是二元變數資料
在進行研究調查時，需要蒐集及分析多個變數的資料，以探究變數間的關聯性。
<br>

## 3.2 常見二元類別變數圖形

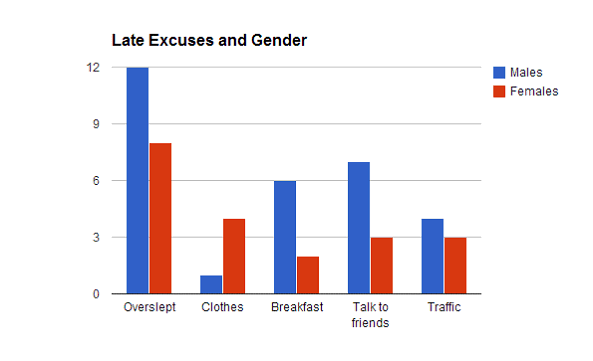
- **Side-by-side Bar Chart** : 將**多類別**資料並列之**條圖**
<br>

- **Stacked Bar Chart** : 將**多類別**相疊再一起之**條圖**
<br>

- **Side-by-side Pie Chart** : 將**多類別**資料並列之**圓餅圖**
<br>

## 3.3 常見二元數值變數圖形

- **二維散佈圖 (x-y Scatter Plot)**
- 觀察到的圖案(直線、曲線、或點隨機分佈)
- 圖案是否**明顯**
- 圖案中是否有**離群值(outlier)**
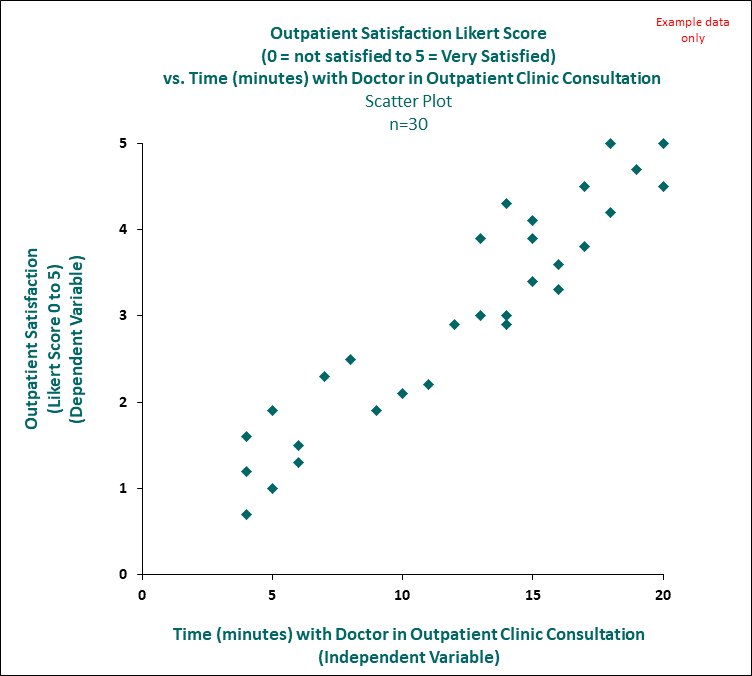<br>

## 3.4 二元數值變亮之量化指標
用來表示兩組數據間**線性**關係的**強弱**及**方向**

- 衡量兩個數值變數間線性**關係**的指標有以下兩種 :
1. **共變異數(Convariance, Cov)**

群體共變異數 : $Cov(x,y) = \sigma_{xy} = \frac{\sum^N_{i=1} (x_i-\mu_x)(y_i-\mu_y)}{N}$<br>
樣本共變異數 : $Cov(x,y) = S_{xy} = \frac{\sum^N_{i=1} (x_i-\bar x)(y_i-\bar y)}{n-1} = \frac{\sum xy - \frac{(\sum x)(\sum y)}{n}}{n-1}$<br>

2. **相關係數 (Correlation Coefficient)**
兩個數值的相關係數是兩變數之共變異數除以各變數之標準差的乘積。

**群體**相關係數 : $p = \frac{Cov(x,y)}{\sigma_x \sigma_y} = \frac{\sigma_{xy}}{\sigma_x \sigma_y}$<br>
**樣本**相關係數 : $r = \frac{Cov(x,y)}{S_x S_y} = \frac{S_{xy}}{S_x S_y}$<br>
$-1 \leq p \leq 1$，$-1 \leq r \leq 1$
越靠近一越強，正表示正線性關係，負表示負線性關係越靠近零越弱。
<br>

## 3.5 x-y 之直線方程式 (迴歸方程式或最小平方線)
x-y 二組數據間如有**線性關係**，則可適配一條**直線**方程式，又稱**迴歸方程式(regression equation)或最小平方線(least-square line)

公式 : **$\hat y = a + bx$**

其中 y 表**dependent** variable, x 表 **independent** variable, a 表 **intercept**截距，b 表**slope**斜率。

公式 : **$b = r(\frac{S_y}{S_x}), a = \bar y - b \bar x$**

<br>

<hr>

# Ch4 機率及機率分佈 Probability and Probability Distributions

## 4.1 機率概念之介紹
### 定義一 : 實驗(Experiment)
實驗是指一個可記錄一些觀察體 (observations) 量測值的過程 (Process)
<br>

### 定義二 : 樣本空間(Sample Space, S)
一個實驗所有可能出現的結果之集合稱為**樣本空間**
<br>

### 定義三 : 事件(Event)
事件為實驗的一個結果

- 簡單事件 (Simple Event)
一個事件若**無法分解**成**兩個**(含)以上其他事件，則此事件稱為**簡單**事件。
- 複合事件 (Compound Event) (Joint event)
一個事件若**能分解**成**兩個**(含)以上其他事件，則此事件稱為**複合**事件。
<br>

### 定義四 : 事件A的機率

**$P(A) = \frac{\#(A)}{\#(S)}$**

其中，$\#(A)$ 表A事件中元素個數，$\#(S)$表示樣本空間中元素個數。

- 機率三原理 :
- 對樣本空間中任一事件A，$0 \leq P(A) \leq 1$
- $P(\emptyset) = 0，P(S) = 1$
- 若$A_1 \cup A_2 \cup ... \cup A_K$ 為**互斥**事件，則 $P(A_1 \cup A_2 \cup ... \cup A_K) = \sum^K_{i=1} P(A_i)$
<br>

## 4.2 條件機率
條件機率 $P(A|B)$ 表在已知 B 事件已發生的條件下 A 事件發生的機率。

$P(A|B) = \frac{P(A \cap B)}{P(B)}$，其中假設 $P(B) > 0$
<br>

## 4.3 貝式定理 (Bays'Theorem)
$P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{P(B|A) \cdot P(A)}{P(B|A) \cdot P(A) + P(B|\bar A) \cdot P(\bar A)}$<br>
$P(B)$ 為全機率 (total probability)