# 李宏毅深度學習教程

## 目錄
[TOC]

---
Github Link : https://github.com/datawhalechina/leedl-tutorial

---

## 第一章 : 深度學習基礎

### 1.1 局部極小值與鞍點
當參數對損失微分為零時，梯度下降就不能再更新參數了，訓練停下來，損失也不會再下降。

梯度為零可能是 : 局部極小值(Local minimum)、局部極大值(Local maximum)、鞍點(Saddle point)，統稱為**臨界點(Critical point)**。

<br>

#### 判斷臨界值種類的方法 :
::: success
**$L(θ') + (θ-θ')^Tg + 1/2(θ-θ')^T H(θ-θ')$**
:::

在泰勒級數近似(Taylor series appoximation)中：
- **$L(θ')$** : 當 $θ$ 與 $θ'$ 很近時，$L(θ)$ 和 $L(θ')$ 應該蠻近的。
- **$(θ-θ')^Tg$** : $g$ 代表梯度(向量)，可以彌補 $L(θ)$ 和 $L(θ')$ 之間的差距，有時會寫成 $\nabla L(θ')$。$g_i$ 是向量 $g$ 的第 $i$ 個元素，$θ$ 的第 $i$ 個元素的微分，即 : $g_i = \cfrac{∂L(θ')}{∂θ_i}$。
- **$\cfrac{1}{2}(θ-θ')^TH(θ-θ')$** : 跟海森矩陣(Hessian matrix) $H$ 有關。$H$ 裡面是二次微分，第 $i$ 行，第 $j$ 列的值 $H_{ij}$ 就是把 $θ$ 的第 $i$ 個元素對 $L(θ')$ 作微分，再把 $θ$ 的第 $j$ 個元素對 $\cfrac{∂L(θ')}{∂θ_i}$ 作微分後的結果，即 : $H_{ij} = \cfrac{∂^2}{∂θ_i∂θ_j}L(θ')$

在臨界點時，梯度 $g$ 為零，因此 $(θ-θ')^Tg$ 為零，所以在臨界點時，損失函數可被近似為 :
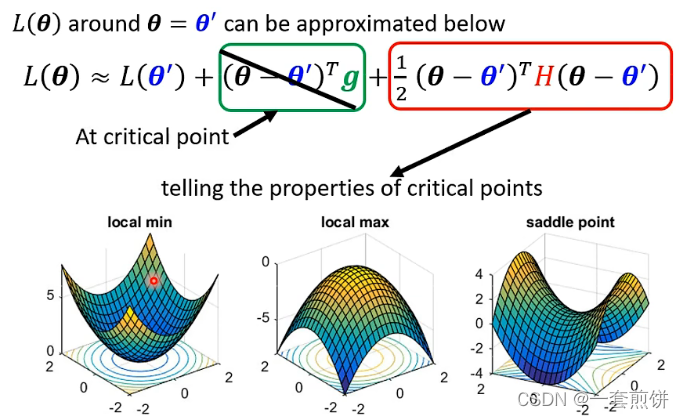
<br>

因此可以根據 **$\cfrac{1}{2}(θ-θ')^T H(θ-θ')$** 來判斷 $θ'$ 附近的誤差表面(Error surface)，$L(θ')$ 的三種情況 :
- $\cfrac{1}{2}(θ-θ')^TH(θ-θ') > 0$ : 局部極小值
- $\cfrac{1}{2}θ-θ')^TH(θ-θ') < 0$ : 局部極大值
- 有時 $\cfrac{1}{2}(θ-θ')^TH(θ-θ') > 0$，有時 $\cfrac{1}{2}(θ-θ')^TH(θ-θ') < 0$ : 鞍點

不過實際上，並不可能帶入全部的 $θ$，因此只要查看 **$H$特徵值**。
若 $H$ 所有特徵值都是正的，則為正定矩陣，臨界點是局部極小值 ; 若 $H$ 所有特徵值都是負的，則為負定矩陣，臨界點是局部極大值 ; $H$ 特徵值有正有負，臨界點是鞍點。

### 1.2 批量和動量
實際上在計算梯度時，是將所有數據分成多個**批量(Batch)**。每次更新參數時，會取出批量大小的資料，計算損失和梯度更新參數。歷遍所有批量的過程，稱為一個**回合(Epoch)**。

<br>

**Best Batch Size** :
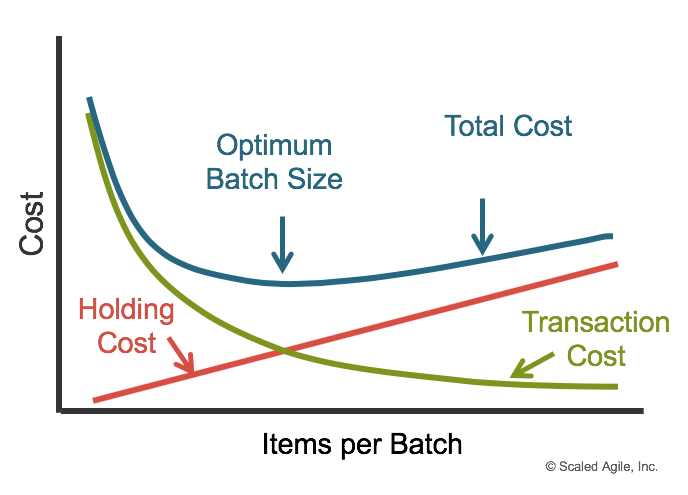
**Situation in Different Batch Size**
<br>

**批量梯度下降(Batch Gradient Descent, BGD) v.s. 隨機梯度下降(Stochastic Gradient Descent, SGD)**

- 批量梯度下降 : 使用全批量(Full batch)數據來更新一次參數
- 隨機梯度下降 : 使用批量大小數據來更新一次參數 (算出來的損失比較有噪聲)

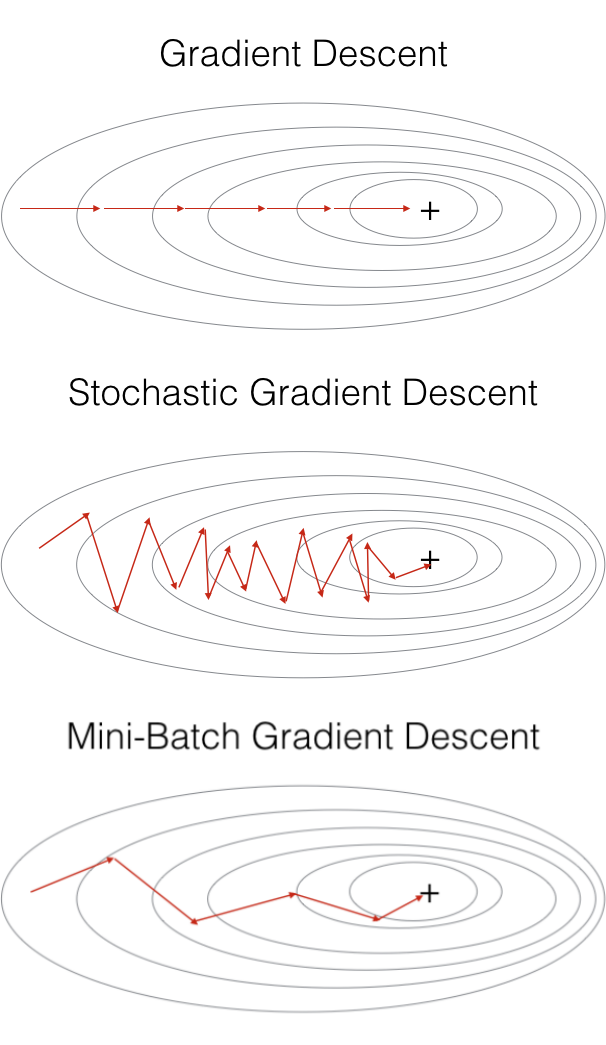
<br>

**隨機梯度下降的梯度上，引入隨機噪聲，因此在非凸優化問題中，相比批量梯度下降，更容易逃離局部極小值。** ($L_1$和$L_2$函數不一樣，梯度不一定等於零)

<br>

在誤差表面中，大的批量大小，傾向於走到「峽谷」(壞的極小值) ; 小的批量大小，傾向於走到「盆地」(好的極小值)，小的批量大小容易跳出峽谷。
<br>

#### 動量法 (Momentum method)
在物理的世界中，一顆球如果從高處滾下來，就算滾到鞍點或是局部極小值，因為慣性的關係，他還是會繼續走。如果將其應用到梯度下降中，就是動量。

一般的梯度下降 :
計算完梯度後，往梯度的反方向去更新參數 $θ_n = θ_{n-1} - ηg_{n-1}$，反覆進行。
<br>

引入動量後的梯度下降 :
不只往梯度的反方向來移動參數，而是**根據梯度的反方向，加上前一步移動的方向**來決定移動方向。更新方向為 $m_n = λm_{n-1} - ηg_{n-1}$ ($n > 0, n = 0$ 則為 $0$)，反覆進行。
<br>

$η$ 是學習率，$λ$ 是前一個方向的權重參數。動量是梯度的負反方向加上前一次移動的方向; 當角度加上動量時，更新的方向不只考慮現在的梯度，而是考慮過去所有梯度的總和。
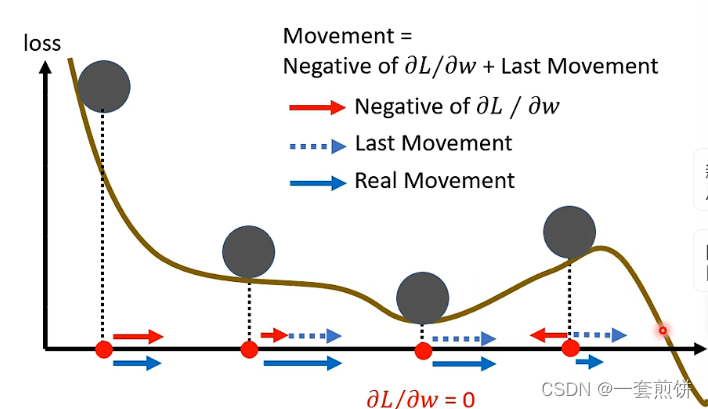
<br>

### 1.3 自適應學習率
當走到臨界點時，代表梯度非常小，但當損失不在下降時，梯度不一定真的很小。梯度可能只是在山谷的兩個谷壁間，不斷來回震盪，損失也不會再下降。
<br>

引入**自適應學習 (Adaptive learning rate)** 的方法給每個參數不同的學習率。如果在某個方向上梯度值小、非常平坦，則會希望學習率調大 ; 若在某個方向非常陡峭、坡度很大，則會希望學習率設小。
<br>

#### 常見的自適應學習率方法
- **AdaGrad** : 在算均方根時，每一個梯度都有同等的重要性。
- **RMSProp** : 在算均方根時，可以調整每個梯度的重要性。
<br>
- **Adam** : 當今最常用的優化器 (optimizer)，RMSProp 加上動量 (Momentum)，其使用動量作為參數更新方向，並能夠自適應調整學習率。

### 1.4 學習率調度
累積很多梯度較小的數值，到一定程度後會「梯度爆炸」，出現暴增的情況，當梯度很大時，$σ$ 會變得很大，學習率就會變很小，參數更新的距離也會變小，暴增的部分就會被修正。使用學習率調度可以解決這個情況。

學習率調度中最常見的策略是**學習率衰減 (learning rate decay)**，隨著參數不斷更新讓 $η$ 越來越小。
<br>
另一個經典的學習率調度方式是**預熱 (warmup)**。預熱方法，是讓學習率先變大後變小，變大、變小的速度是超參數。殘差網路、Bert、Transformer 的訓練都有使用預熱。
<br>

---

## 第二章 : 卷積神經網路 (Convolutional Neural Network, CNN)
每個神經元和輸入向量中的每個數值都需要一個權重，更多的參數為模型帶來更好的彈性和能力，但也增加過擬合(overfitting)的風險。因此考慮到圖像本身的特性，並不一定需要做到全連接網路(fully connected network)。

獨熱向量(One-Hot Vactor) $y'$ 的長度決定模型可以辨識多少不同種類，模型的輸出通過 softmax 後是 $\hat y$，$y'$ 和 $\hat y$ 的交叉熵(cross entropy)越小越好。

### 2.1 Pattern
檢測圖像中有沒有出現重要 pattern，這些 pattern 代表某種特徵。
<br>

### 2.2 Receptive field
每個神經元都只關心自己的 Receptive field。
在下圖中，藍色方框代表 Receptive field，神經元只需要關心這個範圍，把寬、高、通道相乘即為向量，並給每個維度的向量一個權重，最後再加上偏置(Bias)得到輸出。

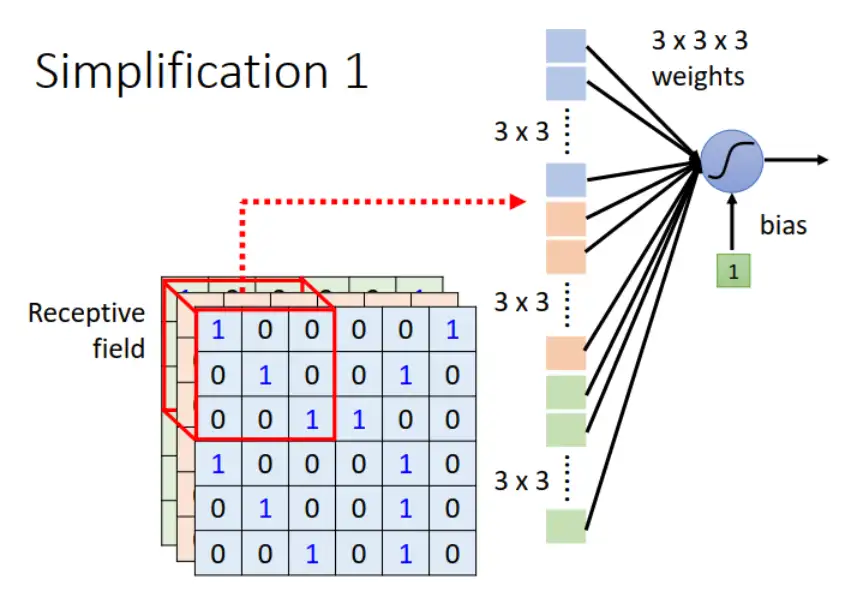
<br>

同個範圍可以有多個不同的神經元 :
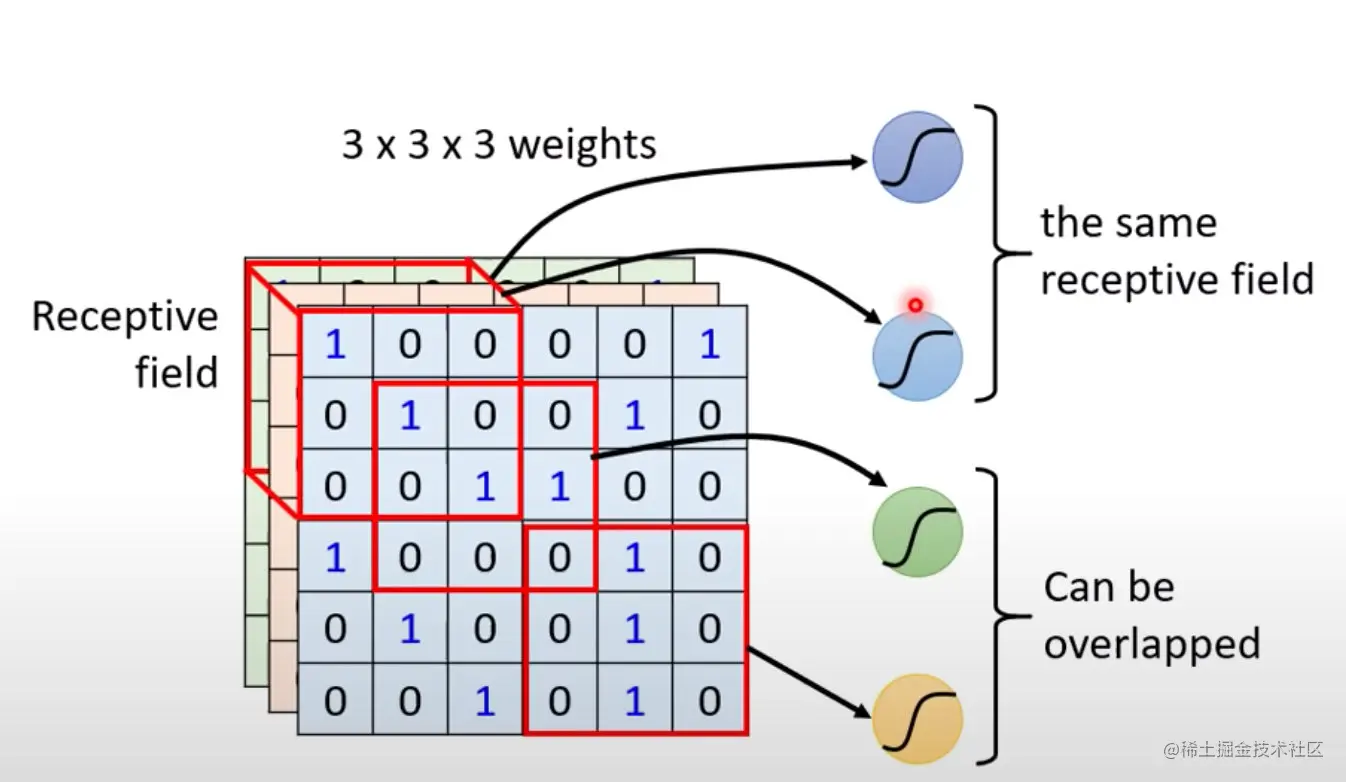
<br>

Receptive field 移動的量叫做步輻(stride)，是一個超參數(hyperparameter)。當 Receptive field 超出圖像範圍時，做填充(padding)，一般使用零填充(zero padding)。
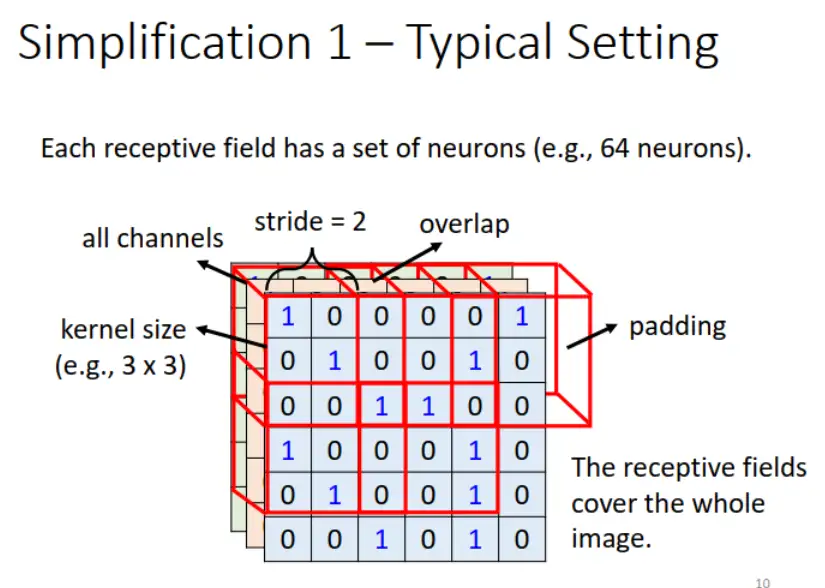
<br>

### 2.3 同樣的 Pattern 可能出現在圖像的不同區域
如果不同的 Receptive field 都要有同樣的檢測神經元，參數量會太多，因此需要簡化。

### 2.4 共享參數(parameter sharing)
儘管兩個神經元的參數是一樣的，但他們的輸入不一樣，Receptive field也會不一樣。

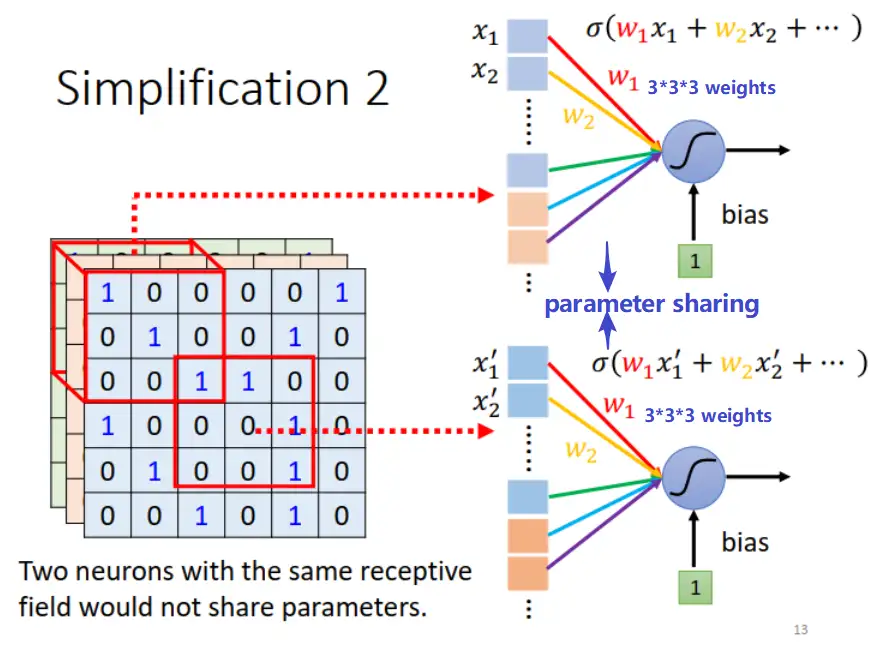
<br>
這些參數稱為濾波器(filter) :
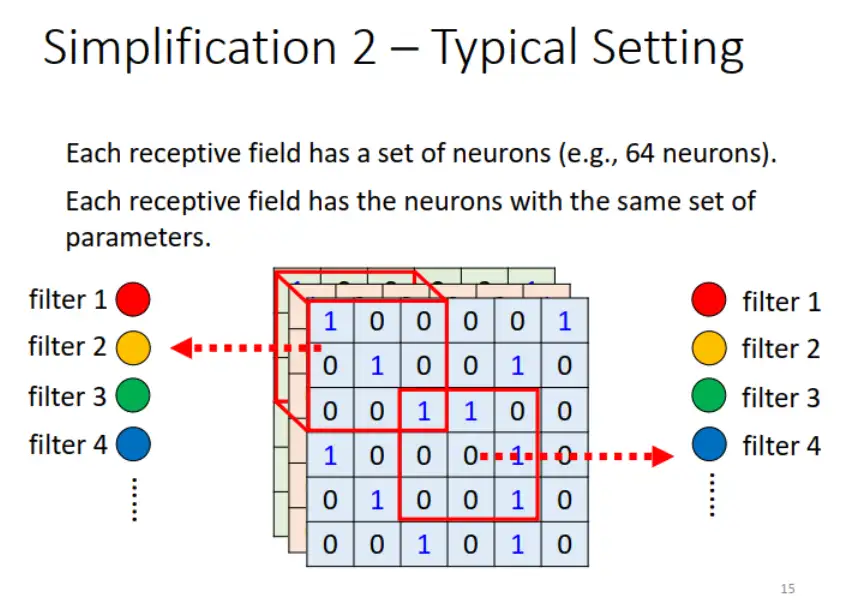
<br>

### 2.5 小結

- 全連接層(Fully connected layer) : 可以決定要看整張圖像還是小範圍。

- 卷積層(Convolutional layer) : Receptive field + Parameter sharing，卷積神經網路的偏差較大，因此靈活度(Flexibility)較低，比較不容易過擬合。

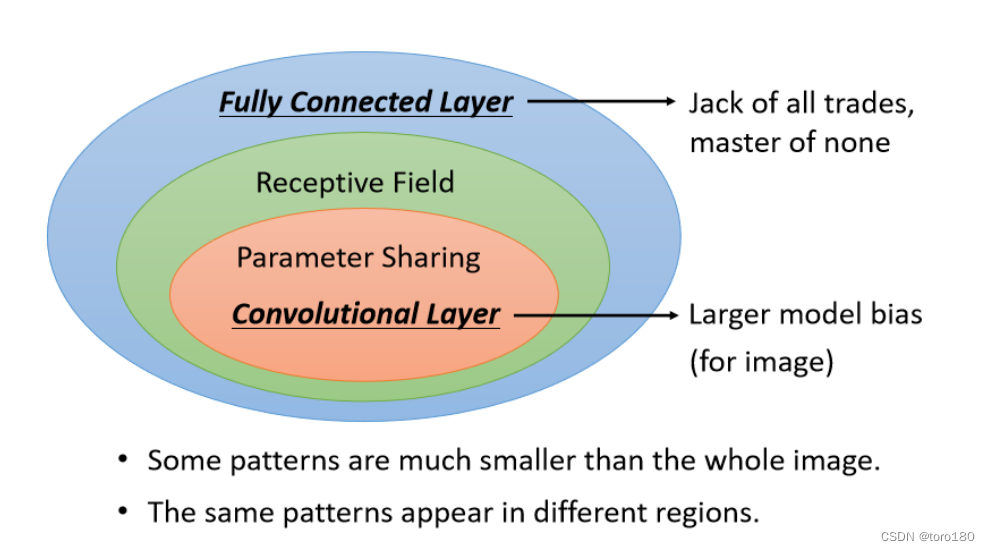
- 當圖像通過卷積層中的所有濾波器後，就會產生一個特徵映像(feature map)。

### 2.6 池化(pooling)
做完卷積後，往往會搭配池化。池化會把圖像變小，一般在實踐上，卷積層會和池化層交替使用。不過池化對於模型的性能(performance)可能會帶來一點傷害，所以近年圖像的網路設計漸漸不採用池化，做全卷積的神經網路。

池化最主要的作用是減少運算量，通過下採樣把圖像變小。
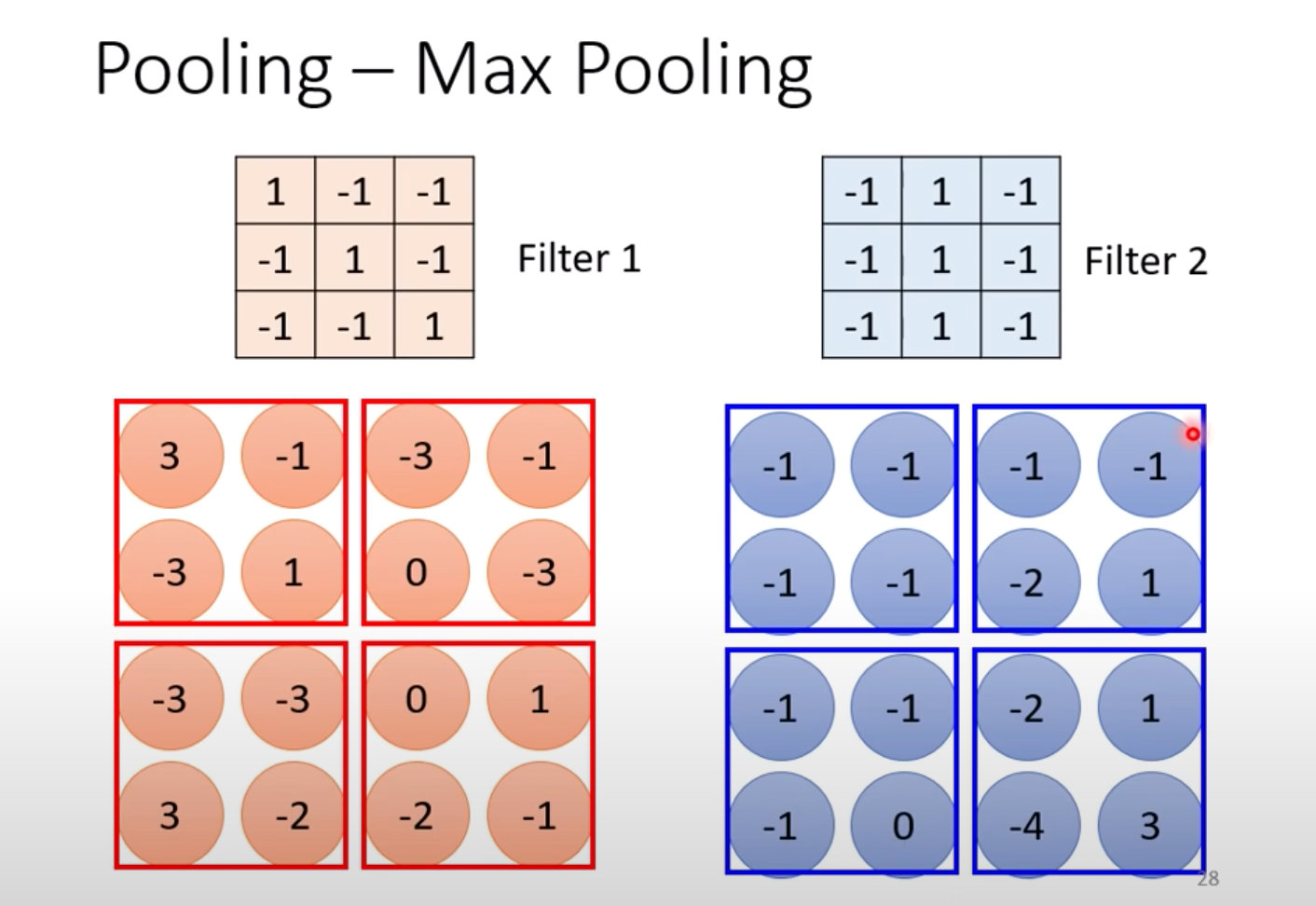
<br>
<br>

在經典的圖像識別網路中，做完幾次卷積層和池化層，會把池化層的輸出做扁平化(flatten)，再把這個向量丟進全連接層，最後再透過 softmax 來得到圖像識別的結果。

---

## 第三章 : 自注意力機制(Self-attention)
輸入可以看作是一個向量，如果是回歸問題，輸出是一個純量 ; 如果是分類問題，輸出是一個類別。

### 3.1 輸入是向量序列的情況

#### 類型 1 : 輸入與輸出數量相同
例子 : 詞性標註(Part-Of-Speech tagging, POS tagging)，判斷該詞是名詞、動詞、形容詞等。

#### 類型 2 : 輸入是一個序列，輸出是一個標籤
例子 : 情感分析(sentiment analysis)，判斷這段話是積極(positive)還是消極(negative)。

#### 類型 3 : 序列到序列
輸入是 $N$ 個向量，輸出是 $N'$ 個向量(由機器決定)。這類任務又稱序列到序列(Sequence to Sequence, Seq2Seq)任務。
例子 : 語音識別。

### 3.2 自注意力的運作原理
考慮整個序列的信息，再來決定應該要輸出什麼樣的結果。

自注意力模型可以疊加很多次，將全連接網路與自注意力模型交替使用，全連接網路專注於某一個位置的信息，自注意力再把整個序列信息再整理一次，"Attention Is All You Need"。

<br>

計算注意力的模塊使用兩個向量作為輸入，輸出數值 $α$，$α$ 即為兩個向量的關聯程度(注意力的分數)。

常見計算 $α$ 的做法是用點積 (dot product)，把輸入的兩個向量分別乘上兩個不同的矩陣，左邊乘上矩陣 $W^q$，右邊乘上矩陣 $W^k$，得到向量 $q$ 和 $k$，再把 $q$ 跟 $k$ 做點積，做逐元素(element-wise)的相乘，全部加起來後就得到一個純量(scalar) $α$。

另一個作法是相加(additive)，把兩個向量通過 $W^q$、$W^k$ 得到 $q$ 和 $k$，(在這步不是做點積)，而是把 $q$ 和 $k$ 相加後，丟進一個 $tanh$ 函數，乘上矩陣 $W$ 得到 $α$。

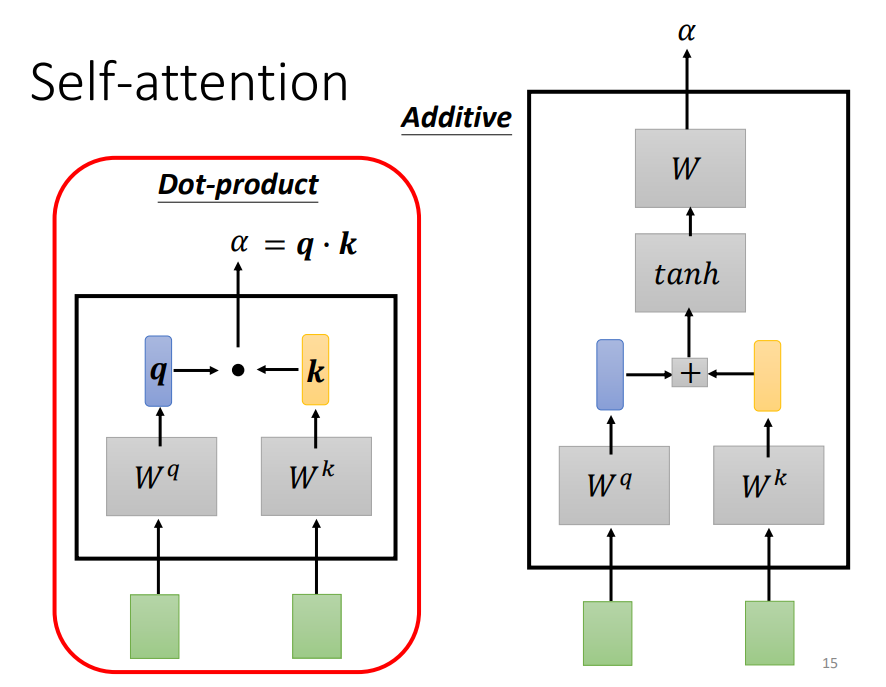
<br>

一般在實踐時，$α^1$ 也會算跟自己的關聯性。接下來對所有關聯性做 softmax 處理，也就是歸一化(normalize)得到 $α'$
**不一定要使用 softmax，也可以使用其他激活函數**

計算 $α^1$ 跟 $α^2$、$α^3$、$α^4$ 之間的關聯性 :
<br>

把向量 $α^1$ 到 $α^4$ 乘上 $W^v$ 得到新向量 : $v^1$、$v^2$、$v^3$、$v^4$，再把每個向量乘上注意力分數 $α'$ 並相加。

如果 $α^1$ 和 $α^2$ 的關聯性很強，即 $α'_{1,2}$ 的值很大。在做加權和(weighted sum)以後，得到的 $b^1$ 的值會比較接近 $v^2$。因此何者的注意力分數最大，其 $v$ 就會主導(dominant) 抽出來的結果。

<br>

每個 $α'$ 都分別產生 $q$、$k$、$v$ :
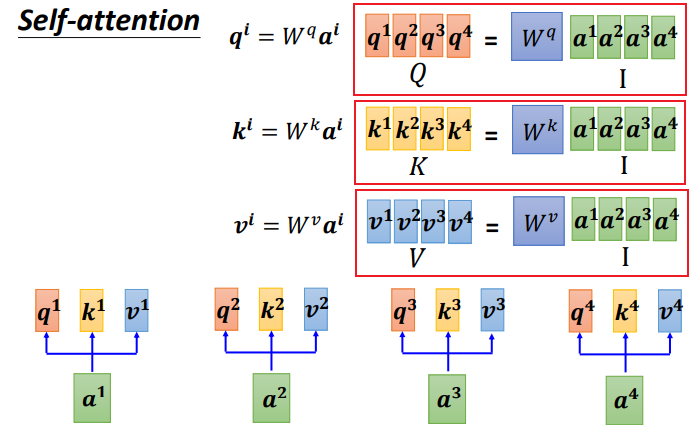
<br>

每一個 $q$ 跟每一個 $k$ 做內積，取得注意力分數，可以看成是 $q^n$ 去乘上 $(k^n)^T$ 矩陣。
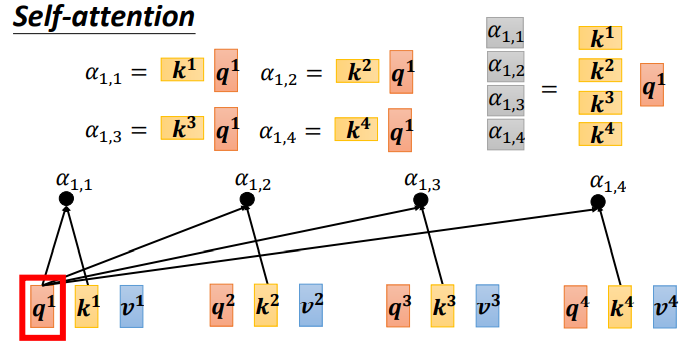
<br>

最後將注意力分數，對 $A$ 每一列做歸一化(normalization)，得到結果 $A'$。
<br>

自注意力的輸入是一組向量，將向量排列後可得矩陣 $I$，輸入 $I$ 分別乘上三個矩陣 : $W^q$、$W^k$、$W^v$，得到三個矩陣 $Q$、$K$、$V$。接下來 $Q$ 乘上 $K^T$ 得到矩陣 $A$，做歸一化後得到 $A'$。
$A'$ 稱為注意力矩陣(attention matrix)，乘上 $V$ 可以得到自注意力層的輸出 $O$。

自注意力層中，唯一需要學習的參數只有 $W^q$、$W^k$、$W^u$，需要通過數據訓練學習出來，其他都是人為設定好的。
<br>

### 3.3 多頭注意力(Multi-head Self-attention)
使用自注意力計算相關性時，用 $q$ 去找相關的 $k$，但相關有很多種不同形式，所以可以有多個 $q$，不同的 $q$ 負責不同種類的相關性，就是多注意力。

<br>

### 3.4 位置編碼(Positional encoding)
位置編碼為每個位置設定一個向量，即位置向量(positional vector)。位置向量用 $e^i$ 表示，上標 $i$ 代表位置。

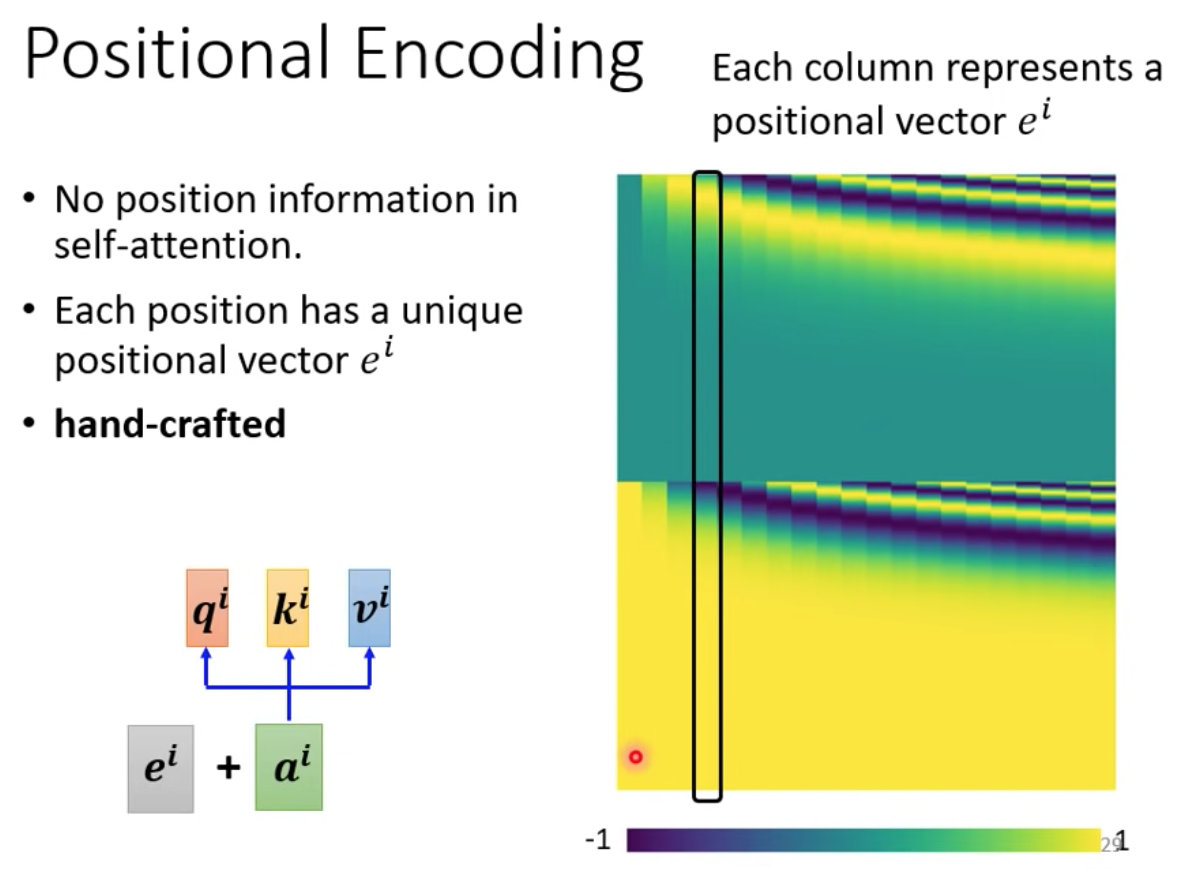
<br>

### 3.5 截斷自注意力(Truncated self-attention)
截斷自注意力指在執行自注意力時，考慮小範圍以代替整體，這樣就可以加快運算速度。

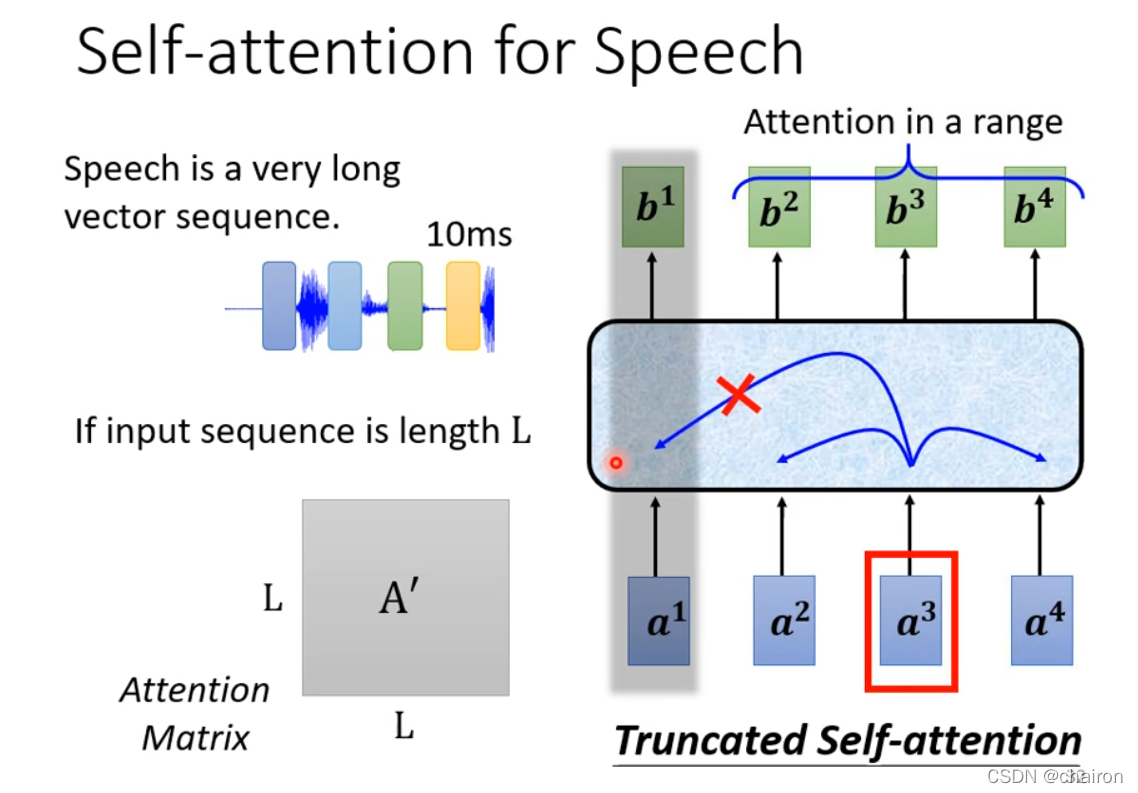
<br>

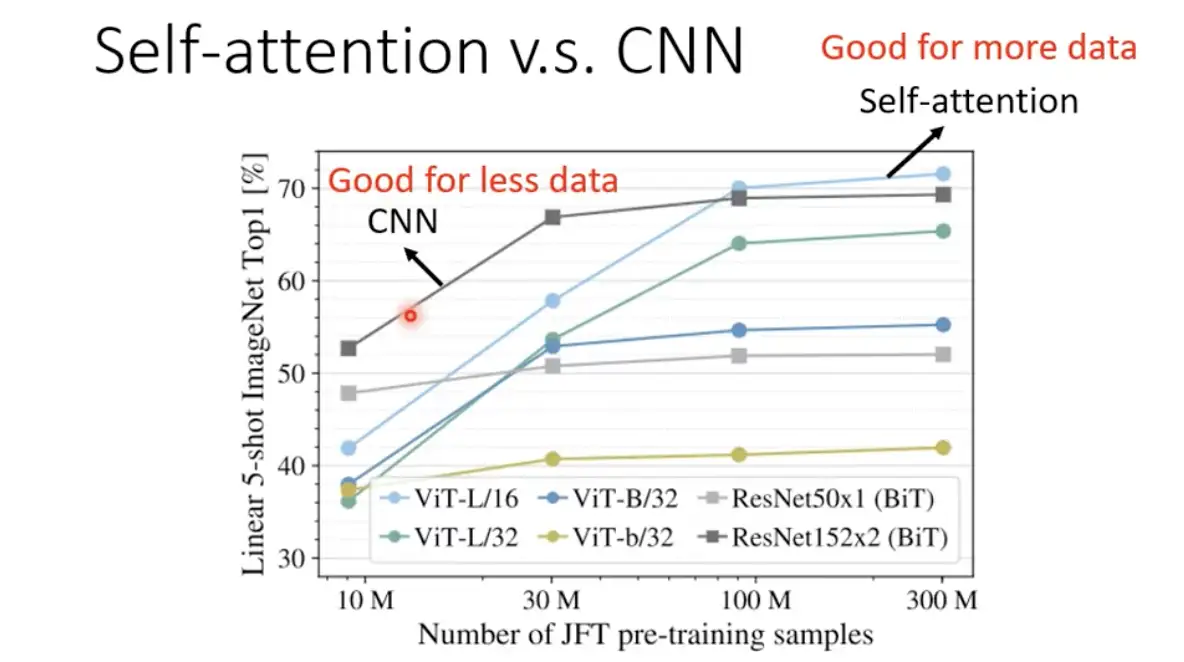
### 3.6 自注意力與卷積神經網路對比
自注意力是靈活的卷積神經網路，卷積神經網路是受限制的自注意力。自注意力的彈性比較大，所以需要比較多的訓練數據，較少的訓練數據會過擬合 ; 而卷積神經網路的彈性較小，在訓練數據少時，結果比較好。

<br>
<br>

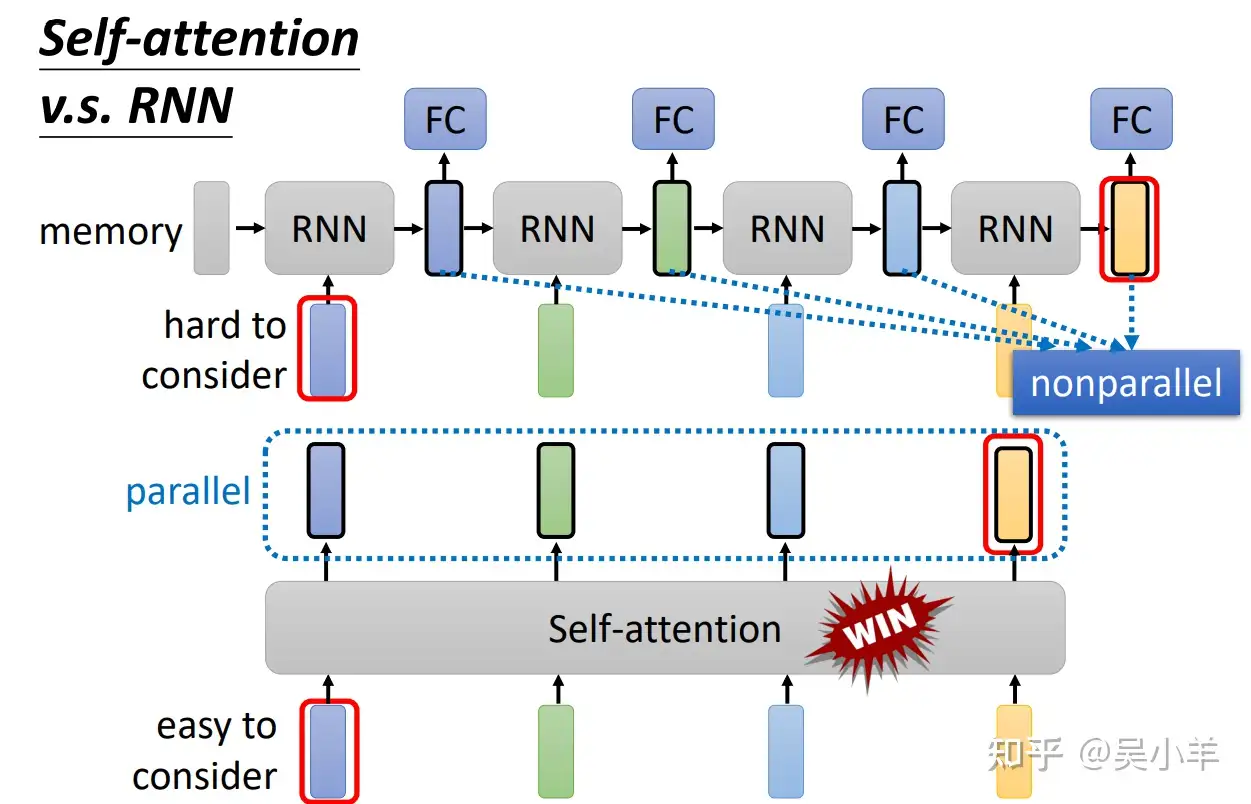
### 3.7 自注意力與循環神經網路對比
循環神經網路(Recurrent Neural Network, RNN)，跟自注意力一樣是處理序列。循環神經網路中，有一個輸入序列、一個隱狀態的向量、一個循環神經網路的區塊(block)，隱狀態儲存歷史信息，可以看做是一種記憶(memory)。
當第二個向量作為輸入時，前一個時間點的輸出也會作為輸入，一起放進循環神經網路產生新的向量，再給全連接網路。

自注意力與循環神經網路的不同在於，**自注意力的每個向量都考慮整個輸入的序列**，而循環神經網路的每個向量只考慮左邊已輸入的向量，沒有考慮右邊的。
但循環神經網路也可以是雙向的，如果用雙向循環神經網路(Bidirectional Recurrent Neural Network, Bi-RNN)，那每一個隱狀態的輸出也是考慮整個輸入的序列。

不過雙向循環神經網路與自注意力在執行上還是有些微差別，對於循環神經網路，最右邊的向量需要考慮左邊的輸入，因此必須把最左邊的輸入存在記憶裡面，一路帶到右邊，才能在最後一個時間點被考慮。在自注意力機制，可以輕易從整個序列上距離遠的向量抽取訊息。另一點是循環神經網路無法並行處理所有輸出，但自注意力可以。

<br>

自注意力也可以用在圖上面，圖可以看作是向量，如果是向量，就可以用自注意力處理。但是自注意力在圖上的應用比較不一樣，除了圖中的節點(node)可以表示成一個向量，還有邊(edge)的信息。

如果節點之間是相連的，**圖上的邊即已經表示了節點與節點之間的關聯性，不需要機器自動找出**。所以將自注意力用在圖上時，計算注意力矩陣只計算有邊相連的節點就好。(沒有相連就不需計算，直接設為 0)
當把自注意力用在圖時，就是一種圖神經網路(Graph Neural Network)。

---

## 第四章 : Transformer

### 4.1 序列到序列模型
Transformer 是一個**序列到序列(Sequence-to-Sequence, Seq2Seq)** 的模型，意即輸入與輸出都是一個序列。輸入與輸出序列長度有兩種，一種是長度一樣，一種是機器決定輸出長度。

### 4.2 序列到序列模型的應用

- **語音辨識、機器翻譯與語音翻譯**

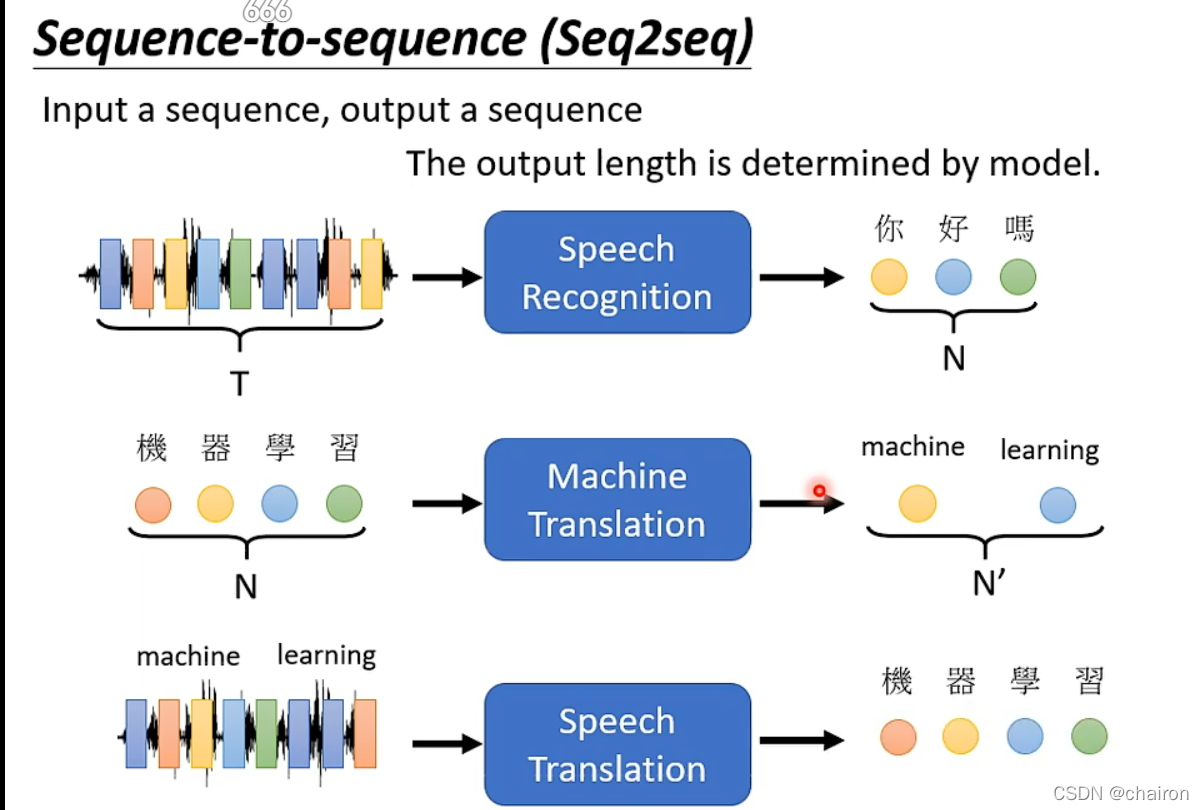
<br>

- **語音合成(Text-To-Speech, TTS)**
目前還沒有端到端(ent-to-end)的模型，使用的模型還是分成兩階段，首先模型把一號文字轉成二號文字，在把二號文字轉成聲音信號(通過序列到序列模型 echotron 實現)。

- **聊天機器人**

- **問答任務**
自然語言處理(Natural Language Processing, NLP)領域應用，例如翻譯、自動摘要情感分析。

- **句法分析(Syntactic parsing)**
在句法分析的任務中，輸入是一段文字，輸出是一個樹狀結構，每個樹狀結構可以看成是一個序列，就可以用序列到序列模型做句法分析。

- **多標籤分類(Multi-label classification)**
多分類問題(multi-class classification)是指分類的類別數大於二，而多標籤分類是指同一個東西可以屬於多個類。

多標籤分類問題不能當作是多分類問題，分類器只會輸出分數最高的答案(儘管取閾值，也只會輸出前幾名)，由於每篇文章對應的類別數量不一樣，因此此方法不可行。所以要用序列到序列模型來做，輸出的類別由機器決定。

### 4.3 Transformer 結構
一般的序列到序列模型會分成**編碼器與解碼器**，編碼器負責處理輸入的序列，在傳遞至解碼器，由解碼器決定輸出的序列。

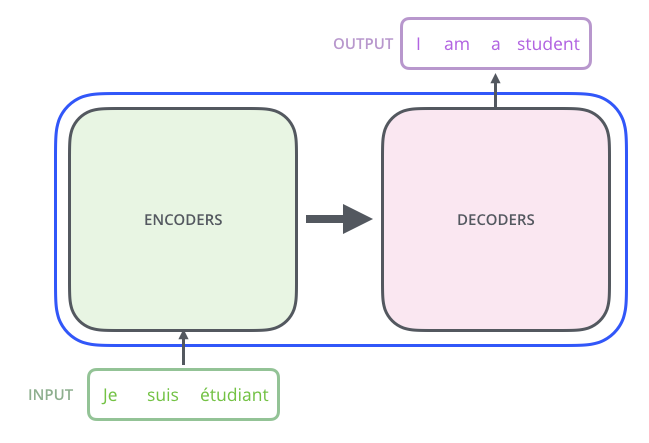
<br>

### 4.4 Transformer 編碼器
Transformer 編碼器使用的是自注意力。
編碼器裡面會分成很多區塊(block)，每一個區塊都是輸入一排向量，輸出一排向量。

<br>

Transformer 編碼器的每個區塊並不是神經網路層，在每個區塊裡，輸入一排向量後做自注意力，考慮整個序列的信息，輸出一排向量，並將其放進全連接網路，輸出另一排向量，這排向量就是區塊的輸出。

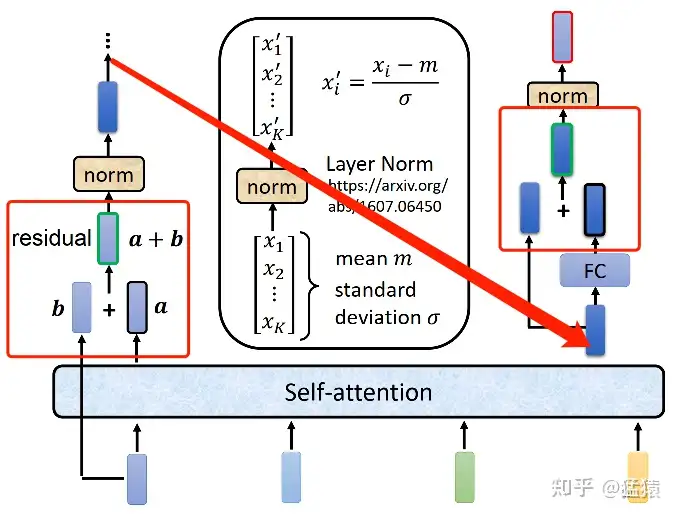
Transformer 加入殘差連接(Residual connection)的設計，最左邊的向量 $b$ 輸入到自注意力層後得到向量 $a$，輸出向量 $a$ 加上其輸入向量 $b$ 得到新的輸出。得到殘差結果以後，在做層歸一化(layer normalization)。

<br>

層歸一化比批量歸一化(batch normalization)簡單，不需要考慮批量(batch)信息。層歸一化會計算輸入向量的均值(mean)和標準差(standard deviation)。

批量歸一化是對不同樣本(example)、不同特徵的同一個維度去計算均值和標準差，但層歸一化是對同一個特徵、同一個樣本裡的不同維度去計算均值跟標準差，接著做歸一化。

輸入向量 $x$ 裡的每一個維度減掉均值 $m$，在除以標準差 $σ$ 以後得到 $x'$ 就是層歸一化的輸出。得到層歸一化的輸出後，將作為全連接網路的輸入，輸入到全連接網路後，還有殘差連接，把全連接網路的輸入跟輸出加起來得到新的輸出，將殘差的結果再做一次層歸一化得到的輸出就是 Transformer 編碼器裡的一個區塊的輸出。

**為什麼 Transformer 使用層歸一化，而不使用批量歸一化?**
經過論文證明在 Transformer 模型裡，批量歸一化不如層歸一化，並提出能量歸一化(power normalization)，能量歸一化甚至比層歸一化好一點。

### 4.5 Transformer 解碼器

- **自回歸解碼器**
解碼器較常見的是自回歸(autoregressive)解碼器。要讓解碼器產生輸出，首先要給定一個代表開始的特殊符號 BOS(Begin Of Sequence)，這是一個特殊的詞元(token)，要讓解碼器停止運作，也需要一個 EOS。

解碼器的輸入是前一個時間點的輸出，並會把自己的輸出當作接下來的輸入，因此解碼器有可能會得到錯誤資訊並產出錯誤輸出，造成誤差傳播(error propagation)。

回顧一下結構圖 :

<br>

類似編碼器，解碼器也有多頭注意力、殘差連接和層歸一化、前饋神經網路，解碼器最後再做 softmax，使其輸出變成一個概率。此外，解碼器使用掩蓋自注意力(masked self-attention)，可以透過一個掩碼(mask)來阻止每個位置選擇其後面的輸入訊息。

原來的自注意力是根據 $a^1$ 到 $a^4$ 的所有信息去輸出 $b^1$，掩蓋自注意力則是產生 $b^1$ 時，只能考慮 $a^1$ 的信息。

**為什麼需要在注意力中掩碼?**
自注意力是 $a^1$ 到 $a^4$ 一次整個輸進去模型，編碼器是一次把 $a^1$ 到 $a^4$　都讀進去，但解碼器是一個一個讀進去的，先讀 $a^1$、再讀 $a^2$... 因此只考慮左邊的東西，沒辦法考慮右邊的。

- **非自回歸解碼器**
非自回歸(non-autoregressive)解碼器有以下優點:
- 平行化
自回歸解碼器是一個一個產生，非自回歸解碼器可以一次產生完整的結果。
- 較能控制輸出長度
用一個分類器決定非自回歸解碼器應該輸出的長度。

平行化是非自回歸解碼器的最大優勢，但性能(performance)往往不如自回歸解碼器。


<br>

### 4.6 編碼器-解碼器注意力
編碼器和解碼器通過編碼器-解碼器注意力(encoder-decoder attention)傳遞信息，是為連接橋梁。解碼器中編碼器-解碼器注意力的鍵和值來自編碼器的輸出，查詢來自解碼器中前一個層的輸出。

### 4.7 Transformer 的訓練過程
解碼器的輸出是一個概率分布，我們要計算標準答案(ground truth)跟分布之間的交叉熵，交叉熵越小越好。
解碼器訓練過程中，在輸入時就給正確答案，希望解碼器的輸出跟正確答案越近越好，稱為教師訓練(teacher forcing)。

### 4.8 序列到序列模型訓練常用技巧

- **複製機制(copy mechanism)**
對很多任務而言，解碼器沒有必要自己創造輸出，例如人名，因此可以從輸入裡複製。

- **引導注意力**
引導注意力會使注意力有一個固定的樣貌，例如注意力位置應該由左到右，最適用於語音識別。

- **束搜索(beam search)**
貪心搜索(greedy search)不一定是最好的，窮舉搜索(exhaustive search)是不現實的。
束搜索用比較有效的方法找一個近似解，但在某些情況下效果不好。適用於答案非常明確，識別結果只有一種可能的任務，反之若是需要發揮一些創造力的任務，束搜索則較沒有幫助。

- **加入噪聲**
在訓練時加入噪聲，讓機器看過更多不同的可能性，會使模型增強魯棒性，較能對抗沒有看過的狀況。

- **使用強化學習訓練**
遇到優化無法解決的問題(無法優化的損失函數)，可以用強化學習訓練(把損失函數當強化學習的獎勵，解碼器當成智能體)。

- **計畫採樣**
在測試時，解碼器看到自己的輸出(會有錯誤)，但在訓練時，解碼器看到是完全正確的，這種不一致現象叫曝光偏差(exposure bias)。
因此不要都給解碼器正確答案，參雜一些錯誤，會讓解碼器學得更好，這叫計畫採樣(sheduled sampling)。

---

## 第五章 : 自監督學習(Self-Supervised Learning, SSL)

## 第六章 : 遷移學習(Transfer learning)

## 第七章 : 強化學習(Reinforcement Learning, RL)