# Key-Recovery Attacks on GCM with Repeated Nonces

# Kiến thức tổng quát

### **Authenticated encryption(AE):**

**Authenticated encryption**(AE) là một sơ đồ mã hóa đồng thời đảm bảo tính bảo mật dữ liệu (còn được gọi là quyền riêng tư: không thể hiểu được tin nhắn được mã hóa nếu không biết khóa bí mật) và tính xác thực (nói cách khác, nó không thể giả mạo: tin nhắn được mã hóa bao gồm một [authentication tag](https://en.wikipedia.org/wiki/Authentication_tag) (thẻ xác thực) mà người gửi chỉ có thể tính toán nếu sở hữu khóa bí mật ). Ví dụ về các chế độ mã hóa cung cấp AE là GCM, CCM.

Nhiều (không phải tất cả) lược đồ AE cho phép tin nhắn chứa "associated data(dữ liệu liên quan)"(AD) không được giữ bí mật nhưng tính toàn vẹn của nó được bảo vệ (nghĩa là nó có thể đọc được nhưng sẽ bị phát hiện giả mạo). Một ví dụ điển hình là tiêu đề của gói mạng chứa địa chỉ đích của nó. Để định tuyến gói tin đúng cách, tất cả các nút trung gian trong đường dẫn tin nhắn cần biết đích đến, nhưng vì lý do bảo mật, chúng không thể sở hữu khóa bí mật. Các lược đồ cho phép dữ liệu liên quan cung cấp mã hóa xác thực bằng dữ liệu liên quan hoặc AEAD.


### **Message authentication code(MAC)**

Trong mật mã, **Message authentication code(**mã xác thực tin nhắn - MAC), đôi khi được gọi là thẻ xác thực (**authentication tag**), là một đoạn thông tin ngắn được sử dụng để xác thực tin nhắn. Nói cách khác, để xác nhận rằng tin nhắn đến từ người gửi đã nêu (tính xác thực của nó) và không bị thay đổi. Giá trị MAC bảo vệ tính toàn vẹn dữ liệu của tin nhắn cũng như tính xác thực của nó bằng cách cho phép người xác minh (người cũng sở hữu khóa bí mật) phát hiện bất kỳ thay đổi nào đối với nội dung tin nhắn.

# The Galois/Counter Mode of Operation (GCM)

GCM là chế độ mã hóa khối được triển khai rộng rãi nhất để xác thực mã hóa với dữ liệu liên quan (AEAD). Về cơ bản nó chỉ là chế độ CTR với một chức năng xác thực gọi là MAC bao bọc quanh nó. Chức năng MAC hoạt động bằng những phép toán học trên một đa thức thuộc $GF(2^{128})$.

(Chi tiết: [https://en.wikipedia.org/wiki/Galois/Counter_Mode#Patents](https://en.wikipedia.org/wiki/Galois/Counter_Mode#Patents))

## Sơ đồ mã hóa


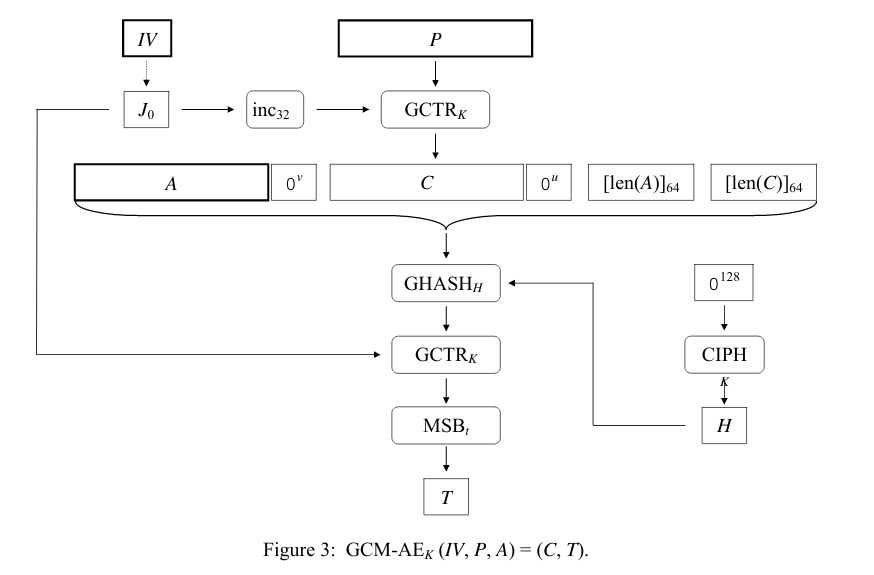
IV bao gồm 96 bit Nonce và 32 bit counter. Vì counter bắt đầu từ 0 và sẽ tăng lên một đơn vị với mỗi block phía sau nên mỗi các block khác nhau cũng có các IV khác nhau.

Quy ước biến:

- $K$ = AES key
- $P$ = plaintext
- $C$ = ciphertext
- $A$ = associated data
- $H = AES(K, 0^{128})$
- $J_0 = Nonce||0^{31}1$
- $EJ = AES(K, J_0)$
- $GHASH_H(X) = H*X \in GF(2^{128})$ với đa thức bất khả quy $x^{128} + x^7 + x^2 + 1$
- $L = Len(A) + Len(C) = L_A + L_C$

Lưu ý: Trong $GF(2^{128})$ phép cộng tương đương với phép xor

→ ta có thể thay thế phép xor bằng phép cộng.

## Giải thích GHASH

Sử dụng các biến đã quy ước ở trên:

Giả sử, ta có:

- C: 32 byte → 2 block, mỗi block 128bit (C1||C2)
- A: 16 byte → 128bit

Để khởi tạo một **authentication tag (**gọi ngắn gọn là tag**) T,** thuật toán sẽ như sau:

$T = (((((((H*A) + C1)*H)+C2)*H)+L)*H)+EJ$

Tương đương với:

$T = A*H^4+C1*H^3+C2*H^2+L*H+EJ$

Ta sẽ khởi tạo đa thưc với H là biến:

$G(X) = A*X^4+C1*X^3+C2*X^2+L*X+EJ$

Và tiến hành tính Tag: T = G(H)

Hacker có thể biết tấn cả các thông số ngoại trừ $H$ và $EJ$

# ****Forbidden Attack****

****Forbidden Attack là**** một cuộc tấn công vào AES-GCM lợi dụng việc sử dụng lại nonce trong quá trình mã hóa. Cuộc tấn công có thể tiết lộ giá trị của $H$, sau đó có thể giúp kẻ tấn công giả mạo thẻ xác thực (**authentication tag**) $T$.

Gỉa sử $G1(X)$ là đa thức trên bản rõ đầu tiên, $G2(X)$ là đa thức trên bản rõ thứ 2 và cả hai bản rõ đều có cùng chiều dài.

$$
G_1(X) = C_{1,1}*X^3 + C_{1,2}*X^2 + L*X+EJ
$$

$$
G_2(X) = C_{2,1}*X^3 + C_{2,2}*X^2 + L*X+EJ
$$

Ta không biết $EJ$ nên không thể tính Tag theo cách thông thương, tuy nhiên nếu ta cộng hai đa thức với nhau ta sẽ được kết quả như sau:

$$
P(X) = (C_{1,1}+C_{1,2})*X^3 + (C_{1,2}+C_{2,2})*X^2 + (L+L)*X+(EJ+EJ)
$$
Vì phép cộng tương đương với phép xor nên: `a + a = a ^ a = 0`
=> đa thức được rút gọn như sau:
$$
P(X) = (C_{1,1}+C_{1,2})*X^3 + (C_{1,2}+C_{2,2})*X^2
$$

Ta sẽ viết lại $P(X)$ như sau:

$$
T1+T2 = (C_{1,1}+C_{1,2})*H^3 + (C_{1,2}+C_{2,2})*H^2
$$

Cuối cùng chuyển vế phương trình đã biến đổi (trong $GF(2^m)$ phép cộng và phép trừ là như nhau)

$$
(C_{1,1}+C_{1,2})*H^3 + (C_{1,2}+C_{2,2})*H^2 + T1+T2 += 0
$$

Như vậy, xét phương trình trên ta đã có tất cả các hệ số trừ H, từ đó ta đơn giản chỉ cần tìm nghiệm của phương trình bậc 3. Việc còn lại chỉ là tìm $H$ trong 3 nghiệm của phương trình.

Sau khi tìm được $H$, ta chỉ việc thế $H$ vào phương trình $T1$ hoặc $T2$ thì sẽ tìm được $EJ$:

$$
EJ = C_{1,1}*H^3 + C_{1,2}*H^2 + L*H + T1
$$

# CTF challenge

## CRYPTOHACK/****SYMMETRIC CIPHERS/FORBIDDEN FRUIT****

source:

from Crypto.Cipher import AES
import os

IV = ?
KEY = ?
FLAG = ?

@chal.route('/forbidden_fruit/decrypt/<nonce>/<ciphertext>/<tag>/<associated_data>/')
def decrypt(nonce, ciphertext, tag, associated_data):
    ciphertext = bytes.fromhex(ciphertext)
    tag = bytes.fromhex(tag)
    header = bytes.fromhex(associated_data)
    nonce = bytes.fromhex(nonce)

    if header != b'CryptoHack':
        return {"error": "Don't understand this message type"}

    cipher = AES.new(KEY, AES.MODE_GCM, nonce=nonce)
    encrypted = cipher.update(header)
    try:
        decrypted = cipher.decrypt_and_verify(ciphertext, tag)
    except ValueError as e:
        return {"error": "Invalid authentication tag"}

    if b'give me the flag' in decrypted:
        return {"plaintext": FLAG.encode().hex()}

    return {"plaintext": decrypted.hex()}

@chal.route('/forbidden_fruit/encrypt/<plaintext>/')
def encrypt(plaintext):
    plaintext = bytes.fromhex(plaintext)
    header = b"CryptoHack"

    cipher = AES.new(KEY, AES.MODE_GCM, nonce=IV)
    encrypted = cipher.update(header)
    ciphertext, tag = cipher.encrypt_and_digest(plaintext)

    if b'flag' in plaintext:
        return {
            "error": "Invalid plaintext, not authenticating",
            "ciphertext": ciphertext.hex(),
        }

    return {
        "nonce": IV.hex(),
        "ciphertext": ciphertext.hex(),
        "tag": tag.hex(),
        "associated_data": header.hex(),
    }

### Solution

Sever cho ta encrypt và decrypt tùy thích nhưng khi encrypt bản rõ có chứa chuỗi con‘flag’ thì chỉ nhận được ciphertext, không nhận được các thành phần còn lại. Ví dụ:

import requests
from pwn import xor
from Crypto.Util.Padding import pad

#@chal.route('/forbidden_fruit/encrypt/<plaintext>/')
def encrypt(plaintext):
    return requests.get(f'https://aes.cryptohack.org/forbidden_fruit/encrypt/{plaintext.hex()}/').json()

#@chal.route('/forbidden_fruit/decrypt/<nonce>/<ciphertext>/<tag>/<associated_data>/')
def decrypt(nonce, ciphertext, tag, associated_data):
    return requests.get(f'https://aes.cryptohack.org/forbidden_fruit/decrypt/{nonce}/{ciphertext}/{tag}/{associated_data}').json()

print(encrypt(pad(b'a',16)))
print(encrypt(pad(b'give me the flag', 16)))

Ta sẽ nhận được output như sau:

{'associated_data': '43727970746f4861636b', 'ciphertext': '40668a7ee83beb1adc3a4ba60f9e99c7', 'nonce': 'd37388ce56af78cfbc922683', 'tag': '0aa50c4cea6fe576fe72a8ca3c9a7b68'}
{'ciphertext': '4600f314c7598135a75d218966fdf7af99025304231bc044b5211e5f1563946d', 'error': 'Invalid plaintext, not authenticating'}

Ta có thể tái sử dụng `associated_data` và `nonce` vì chúng được giữ nguyên. Mục đích của ta là tìm `tag` của chuỗi `give me the flag` sau khi được mã hóa. Giống hệt như kịch bản đã nêu ở trên. Lúc này ta dang trong vai hacker, sở hữu tất cả các tham số trừ `H` và `EJ`. Bây giờ, chỉ cần áp dụng lý thuyết đã được giải thích ở trên vào challenge này.

Đầu tiên, ta sẽ gửi 2 thông điệp bất kì không chứa chuỗi con `flag` và nhận uotput mà sever trả về:

payload1 = b'a'*32
payload2 = b'b'*32

print(encrypt(payload1))
print(encrypt(payload2))

Output:

{'associated_data': '43727970746f4861636b', 'ciphertext': '4008e41086558574b25425c861f0f7a9e8732275526ab135c4506f2e6412e51c', 'nonce': 'd37388ce56af78cfbc922683', 'tag': '3add4bcab3dc6285b556ba75a659947b'}
{'associated_data': '43727970746f4861636b', 'ciphertext': '430be71385568677b15726cb62f3f4aaeb7021765169b236c7536c2d6711e61f', 'nonce': 'd37388ce56af78cfbc922683', 'tag': '501976ec05644211fd671f1c69f2bff2'}

Bây giờ ta sẽ khôi phục H và tìm tag cho thông điệp `give me the flag`

(sử dụng code có sẵn ở: [https://meowmeowxw.gitlab.io/ctf/utctf-2020-crypto/](https://meowmeowxw.gitlab.io/ctf/utctf-2020-crypto/))

from Crypto.Util.number import long_to_bytes as lb
from Crypto.Util.number import bytes_to_long as bl
from binascii import unhexlify, hexlify
from sage.all import *
import struct

def bytes_to_polynomial(block, a):
    poly = 0 
    # pad to 128
    bin_block = bin(bl(block))[2 :].zfill(128)
    # reverse it to count correctly, wrong don't reverse it lol
    # bin_block = bin_block[::-1]
    for i in range(len(bin_block)):
        poly += a^i * int(bin_block[i])
    return poly

def polynomial_to_bytes(poly):
    return lb(int(bin(poly.integer_representation())[2:].zfill(128)[::-1], 2))

def convert_to_blocks(ciphertext):
    return [ciphertext[i:i + 16] for i in range(0 , len(ciphertext), 16)]

def xor(s1, s2):
    if(len(s1) == 1 and len(s1) == 1):
        return bytes([ord(s1) ^^ ord(s2)])
    else:
        return bytes(x ^^ y for x, y in zip(s1, s2))

F, a = GF(2^128, name="a", modulus=x^128 + x^7 + x^2 + x + 1).objgen()
R, x = PolynomialRing(F, name="x").objgen()

# Set correct values
C1 = convert_to_blocks(bytes.fromhex("4008e41086558574b25425c861f0f7a9e8732275526ab135c4506f2e6412e51c"))
T1 = bytes.fromhex("3add4bcab3dc6285b556ba75a659947b")
C2 = convert_to_blocks(bytes.fromhex("430be71385568677b15726cb62f3f4aaeb7021765169b236c7536c2d6711e61f"))
T2 = bytes.fromhex("501976ec05644211fd671f1c69f2bff2")
C3 = convert_to_blocks(bytes.fromhex("4600f314c7598135a75d218966fdf7af99025304231bc044b5211e5f1563946d"))

L = struct.pack(">QQ", 0 * 8, len(C1) * 8)
C1_p = [bytes_to_polynomial(C1[i], a) for i in range(len(C1))]
C2_p = [bytes_to_polynomial(C2[i], a) for i in range(len(C2))]
C3_p = [bytes_to_polynomial(C3[i], a) for i in range(len(C3))]
T1_p = bytes_to_polynomial(T1, a)
T2_p = bytes_to_polynomial(T2, a)
L_p = bytes_to_polynomial(L, a)
# Here G_1 is already modified to include the tag
G_1 = (C1_p[0] * x^3) + (C1_p[1] * x^2) + (L_p * x) + T1_p
G_2 = (C2_p[0] * x^3) + (C2_p[1] * x^2) + (L_p * x) + T2_p
G_3 = (C3_p[0] * x^3) + (C3_p[1] * x^2) + (L_p * x)
P = G_1 + G_2
auth_keys = [r for r, _ in P.roots()]
for H, _ in P.roots():
    EJ = G_1(H)
    T3 = G_3(H) + EJ
    print("H: " + str(H) + "\nT3: " + str(polynomial_to_bytes(T3).hex()))

Output như sau:

H: a^126 + a^125 + a^124 + a^122 + a^120 + a^119 + a^117 + a^116 + a^115 + a^114 + a^107 + a^101 + a^99 + a^98 + a^97 + a^95 + a^93 + a^92 + a^90 + a^87 + a^86 + a^84 + a^83 + a^82 + a^81 + a^80 + a^76 + a^75 + a^71 + a^66 + a^64 + a^63 + a^62 + a^60 + a^56 + a^54 + a^53 + a^49 + a^48 + a^47 + a^46 + a^44 + a^43 + a^41 + a^40 + a^36 + a^33 + a^31 + a^24 + a^22 + a^21 + a^19 + a^18 + a^16 + a^15 + a^14 + a^13 + a^8 + a^7 + a^5 + 1 
T3: 8c7b37c02480f38bee660f61448d6c7b
H: a^127 + a^120 + a^119 + a^118 + a^117 + a^116 + a^115 + a^110 + a^108 + a^107 + a^105 + a^104 + a^101 + a^100 + a^99 + a^97 + a^96 + a^94 + a^93 + a^90 + a^87 + a^86 + a^85 + a^83 + a^82 + a^81 + a^79 + a^78 + a^74 + a^73 + a^71 + a^69 + a^68 + a^67 + a^65 + a^63 + a^62 + a^60 + a^58 + a^57 + a^56 + a^55 + a^49 + a^48 + a^47 + a^46 + a^45 + a^42 + a^41 + a^40 + a^37 + a^36 + a^31 + a^30 + a^29 + a^28 + a^27 + a^25 + a^22 + a^19 + a^13 + a^11 + a^10 + a^9 + a^8 + a^4 + a^2   
T3: 48c02959b58c7ecca33e43687c4f9ed4
H: a^127 + a^126 + a^125 + a^124 + a^122 + a^118 + a^114 + a^110 + a^108 + a^105 + a^104 + a^100 + a^98 + a^96 + a^95 + a^94 + a^92 + a^85 + a^84 + a^80 + a^79 + a^78 + a^76 + a^75 + a^74 + a^73 + a^69 + a^68 + a^67 + a^66 + a^65 + a^64 + a^58 + a^57 + a^55 + a^54 + a^53 + a^45 + a^44 + a^43 + a^42 + a^37 + a^33 + a^30 + a^29 + a^28 + a^27 + a^25 + a^24 + a^21 + a^18 + a^16 + a^15 + a^14 + a^11 + a^10 + a^9 + a^7 + a^5 + a^4 + a^2        
T3: fd6ab9e0d050978f857c4a859386ad5a

Thử lần lượt T3 với vai trò là tag và gửi lên sever với chế độ decrypt thì sẽ thu được flag.

crypto{https:...}

### References

[https://meowmeowxw.gitlab.io/ctf/utctf-2020-crypto/](https://meowmeowxw.gitlab.io/ctf/utctf-2020-crypto/)

[https://en.wikipedia.org/wiki/Galois/Counter_Mode#Patents](https://en.wikipedia.org/wiki/Galois/Counter_Mode#Patents)