# 資料結構(sparse table, BIT, segment tree)
## Sparse Table
### RMQ 問題
> 給定一個$n$項的陣列，然後會有$q$筆詢問，第$i$筆詢問要輸出第$l_i$項到第$r_i$項的最小值

模板題：<a href="https://cses.fi/problemset/task/1647/">CSES Static Range Minimum Queries</a>
### 想法
把區間$[L, R]$拆成兩個大小為$2^x(0\leq x\leq\lfloor\log_2 n\rfloor)$的區間，透過預處理所有可能的大小為$2^x$的區間，可以達到預處理$O(n\log n)$、每筆詢問$O(1)$求值。

對於所有可能的大小為$2^x$的區間$[L, R]$，我們可以把他改寫成$[L, L + 2^x)$，因為$L+2^x\leq n+1$，
因此所有可能的區間$[L, L + 2^x)$的數量為$n+(n-1)+(n-2)+(n-4)+\dots +(n-2^{\lfloor\log_2 n\rfloor})=O(n\log n)$個區間。

如何對於任意的區間$[L,R]$都求出它的答案？
找到一個$x$使得$[L, L + 2^x) \bigcup (R - 2^x, R] = [L, R]$即可！
那麼當$x=\lfloor\log_2 (R-L+1)\rfloor$時，上式永遠成立！

### 實作
只要用for迴圈就可以跑過所有可能的區間了。
::: spoiler AC code

#include <bits/stdc++.h>
using namespace std;

int main(){
	int n, q;
	cin >> n >> q;
	vector<int> arr(n);
	for(int i = 0; i < n; i++){
		cin >> arr[i];
	}
	int logn = __lg(n);
	vector<vector<int>> mn(logn + 1, vector<int>(n));
	for(int i = 0; i < n; i++){
		mn[0][i] = arr[i];
	}
	for(int i = 1; i <= logn; i++){ // 計算大小為2^i的區間最小值
		int pre_len = 1 << (i-1);
		for(int j = 0; j + pre_len < n; j++){
			mn[i][j] = min(mn[i-1][j], mn[i-1][j+pre_len]);
		}
	}
	while(q--){
		int ql, qr;
		cin >> ql >> qr;
		ql--; qr--;
		int lg = __lg(qr-ql+1); // 取log的函式(回傳整數)
		int len = 1 << lg;
		cout << min(mn[lg][ql], mn[lg][qr+1-len]) << "\n";
	}
	return 0;
}

:::
<!--
#include <bits/stdc++.h>
using namespace std;
int main(){
int n,q;
cin>>n>>q;
vector <int> arr(n);
for(int i=0;i<n;i++){
cin>>arr[i];
}
vector <vector <int> > mn(20,vector <int>(n));
for(int i=0;i<n;i++){
mn[0][i]=arr[i];
}
for(int i=0;i+1<20;i++){
int len = 1 << i;
for(int j=0;j+len<n;j++){
mn[i+1][j]=min(mn[i][j],mn[i][j+len]);
}
}
while(q--){
int ql,qr;
cin>>ql>>qr;
ql--,qr--;
int lg=__lg(qr-ql+1);
int len = 1 << lg;
cout<<min(mn[lg][ql],mn[lg][qr+1-len])<<"\n";
}
return 0;
} -->

<!-- TO DO -->

## 例題
<a href="https://zerojudge.tw/ShowProblem?problemid=d539">ZJ d539 區間 MAX</a>

## BIT
### 資結中毒
當你學會BIT、線段樹等強力資料結構的時候，你會有一段時間**看到什麼題目都想要把資結砸下去**，
這時就稱為資結中毒，會寫這段是要提醒你們，**用資結之前一定要先三思**，
儘管它很好用，把它刻出來還是需要一點時間，而且有些題目會故意卡它的複雜度或是記憶體，讓你過不了。
### 單點修改區間求和問題
> 給定一個$n$項的陣列，然後會有$q$筆操作，每個操作會輸入一行，
> 格式為：「$1$ $x$ $val$」或「$2$ $l$ $r$」，
> 分別代表「使陣列第$x$項的值增加$val$（這項操作不須輸出）」
> 與「輸出目前陣列第$l$項到第$r$項的總和」
模板題：<a href="https://cses.fi/problemset/task/1648/">CSES Dynamic Range Sum Queries</a>

### 區間修改單點求和問題
> 給定一個$n$項的陣列，然後會有$q$筆操作，每個操作會輸入一行，
> 格式為：「$1$ $l$ $r$ $val$」或「$2$ $x$」，
> 分別代表「使陣列第$l$項到第$r$項每一項的值都增加$val$（這項操作不須輸出）」
> 與「輸出目前陣列第$x$項的值」
模板題：<a href="https://cses.fi/problemset/task/1651">CSES Range Update Queries</a>
### 問題分析
如果是一次做完所有修改再一次詢問，那麼用前綴和就可以了，但是這兩題都是要求在線
（邊修改邊輸出）的，所以行不通，這時就要使用BIT(Fenwick Tree)了，
它可以有效解決這兩個問題，複雜度$O((n+q)\log n)$。
至於區間修改區間求和問題，則需要開兩棵BIT或是使用線段樹，
線段樹會在之後的章節提到，而兩棵BIT的做法請參考<a href="https://cp.wiwiho.me/fenwick-tree/#%E6%87%89%E7%94%A8">wiwiho的文章</a>。
### 模板

### 原理
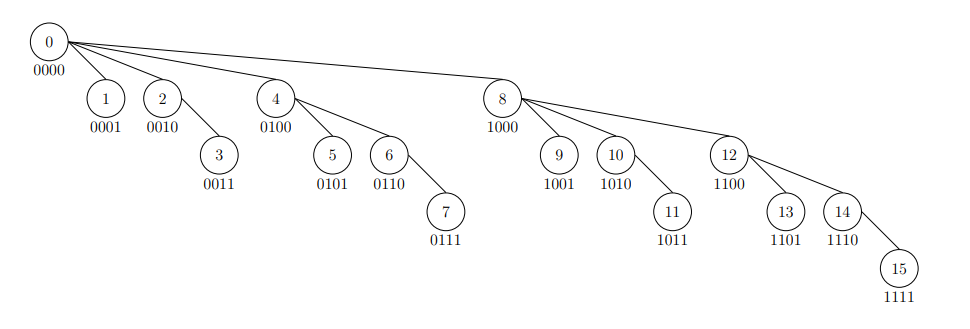
<a href="https://cp.wiwiho.me/fenwick-tree/">圖片來源</a>
說真的，原理不是很重要，會用就好。
::: spoiler 測試用code
<a></a>
qry函式和upd函式的複雜度都是$O(\log n)$。

#include <bits/stdc++.h>
using namespace std;

const int N = (int)(2e5) + 10;
int n;
long long BIT[N];

void upd(int x, long long val){ // 修改
    if(x == 0) return;
    for(; x <= n; x += (x)&(-x)){
        BIT[x] += val;
    }
    return;
}

long long qry(int x){ // 查值
    long long ret = 0;
    for(; x > 0; x -= (x)&(-x)){
        ret += BIT[x];
    }
    return ret;
}

int main(){
    cin >> n;
    for(int i = 1; i <= n; i++) cout << qry(i) << " "; cout << endl;
    while(true){
        int tmp;
        cin >> tmp;
        upd(tmp, 1);
        for(int i = 1; i <= n; i++) cout << qry(i) << " "; cout << endl;
    }
    return 0;
}

:::
<a></a>
可以看到兩個函數裡面都有出現`x&(-x)`，基本上這就是BIT的精隨，對應上面的圖片，
`x-=x&(-x)`就相當於朝樹的根節點移動，而`x+=x&(-x)`就相當於朝樹的葉節點移動。

實際測試之後會更了解它的用法。

注意：使用BIT時只能使用1-base，不然可能會造成無限迴圈（在update時），上面的code是有刻意把這個case判掉的。

### 使用方法
經過一點測試，可以發現如果對BIT的一個位置做操作，那麼對它後面（還有它本身）的位置所query出來的結果都會有所改變，而它前面的位置query出來的值則是一模一樣。
這樣就可以解釋為什麼BIT可以做到「區間修改單點查詢」以及「單點修改區間查詢」了。

如果要做到「區間修改單點查詢」，那麼就把$qry(i)$的值當成是陣列第$i$項的值，而$upd(i, val)$就相當於把陣列的第$i$項還有它後面的每一項全部增加$val$。

如果要做到「單點修改區間查詢」，那麼$upd(i, val)$就相當於使陣列第$i$項增加$val$，而$qry(i)$的值就是陣列前$i$項的前綴和（第1項到第i項的總和），而區間$[l, r]$的總和就是$qry(r)-qry(l-1)$。

### 實作細節
如果因為數字太大而需要取mod，要注意區間和可能相減變成負的，
因為a>b不代表a%MOD>b%MOD。
輸出時記得改成`cout << ((qry(r)-qry(l-1)) % MOD + MOD) % MOD;`，這樣保證不會輸出負數。

寫一個把BIT的每一項的query都輸出的函式並不需要多少時間，寫了還能省下不少debug時間。

### 例題
<a href="https://zerojudge.tw/ShowProblem?problemid=d799">ZJ d799 區間求和</a>
<a href="https://zerojudge.tw/ShowProblem?problemid=d788">ZJ d788 排名順序</a>
<a href="https://zerojudge.tw/ShowProblem?problemid=d794">ZJ d794 世界排名</a>
## 線段樹

模板題：<a href="https://cses.fi/problemset/task/1649/">CSES Dynamic Range Minimum Queries</a>

線段樹是一種處理對於區間的動態修改與查詢的資料結構，可以在$O(\log n)$的時間複雜度完成單點修改，區間修改，區間查詢，而線段樹不管是查詢還是修改，最主要就是利用分治去求解，每次都把所求序列分成兩部分，分到可以直接查詢答案後再回傳

<a href="https://hackmd.io/@wiwiho/cp-note/%2F%40wiwiho%2FCPN-segment-tree">圖片來源</a>

### 建構

我們現在想要建構所以圖上區間$[L, R]$的答案
如果$L=R$，就直接查詢該值並回傳
否則就往左子節點$[L, \lfloor\frac{L+R}{2}\rfloor]$和右子節點$[\lfloor\frac{L+R}{2}\rfloor+1,R]$查詢，並將兩節點的答案合併

### 查詢

當我們要查詢區間$[ql, qr]$的答案，而目前節點對應的資訊是$[L, R]$
如果$[L, R]$完整被$[ql, qr]$包含$(ql\leq L\leq R\leq qr)$，那麼直接提取$[L, R]$的值
如果$[L, R]$跟$[ql, qr]$沒有交集$(ql>R 或 qr>L)$那就直接退出該區間
否則就往左子節點和右子節點查詢，並將兩節點的答案合併

### 單點修改

如果我們要在位置$p$上做修改，而目前節點對應的資訊是$[L, R]$
如果$L=R$，就直接做修改
否則要修改的節點一定會在左子節點$[L, \lfloor\frac{L+R}{2}\rfloor]$和右子節點$[\lfloor\frac{L+R}{2}\rfloor+1,R]$之一，在決定要往哪邊做遞迴，更新該節點

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 100005;
int n;
ll sg[MAX_N * 4] = {0}, a[MAX_N] = {0};

ll build(int L, int R, int v) {
    if (L == R) return sg[v] = a[L];
    int M = L + R >> 1;
    return sg[v] = build(L, M, v << 1) + build(M + 1, R, v << 1 | 1);
}

ll query(int ql, int qr, int L, int R, int v) {
    if (ql <= L && R <= qr) return sg[v];
    int M = L + R >> 1;
    if (qr <= M) return query(ql, qr, L, M, v << 1);
    if (M < ql) return query(ql, qr, M + 1, R, v << 1 | 1);
    return query(ql, M, L, M, v << 1) + query(M + 1, qr, M + 1, R, v << 1 | 1);
}

ll modify(int p, ll val, int L, int R, int v) {
    if (L == R) return sg[v] = val;
    int M = L + R >> 1;
    if (p <= M) return sg[v] = modify(p, val, L, M, v << 1) + sg[v << 1 | 1];
    return sg[v] = sg[v << 1] + modify(p, val, M + 1, R, v << 1 | 1);
}

int main() {
    n = 8;
    int aa[9] = {0, 5, -3, 2, 6, 9, -4, 3, 2};
    for (int i = 1; i <= n; ++i) a[i] = aa[i];
    build(1, n, 1);
    for (int i = 1; i < 16; ++i) cout << sg[i] << ' ';
    cout << endl << "query of 3 to 5: " << query(3, 5, 1, n, 1);
}