HackMD - Collaborative Markdown Knowledge Base

> ( •̀ ω •́ )✧ 이 글은 논문과 코드를 맵핑하여 이해하기 위해 작성했습니다. 보완이 필요한 내용은 댓글 부탁드립니다. > > 📖 **Reference** > - [논문 : Variational Autoencoders for Collaborative Filtering ](https://arxiv.org/abs/1802.05814) > - https://github.com/dawenl/vae_cf > - https://github.com/younggyoseo/vae-cf-pytorch > - [이성범님 Paper-Code-Review-2018-WWW-Variational-Autoencoders-for-Collaborative-Filtering](https://velog.io/@2712qwer/Paper-Code-Review-2018-WWW-Variational-Autoencoders-for-Collaborative-Filtering) > - [Alfredo Canziani - 생산적 모델 - 변이형 오토인코더](https://atcold.github.io/pytorch-Deep-Learning/ko/week08/08-3/) ## 00. 사전 지식 ### 1 ) 다항 분포 ( Multinomial distribution ) 각각의 　독립적인 시행　 에서 나올 수 있는 값이 ${k}$ 가지 이고, 　각 값이 나타날 확률　은 ${p_i, p_2, ..., p_k}$ 일 때, ${n}$ 번의 시행에서 ${i}$ 번째 값이 　특정 횟수　 ${x_i}$번 　만큼 나타날 확률　 ( ${x_i+x_2+...+x_k = n )}$ ### 2 ) VAE ( Variational Auto-Encoder ) > `참고` Auto Encoder 는 input 에서 feature 를 뽑고 output 을 만드는 모델이지만, VAE 는 ${p_{\theta}(x)}$ 를 최대화하는 generative model 이다. ( ${x}$는 ${P_{data}}$ 에서 샘플링됨 ) <img src="https://velog.velcdn.com/images/hobbang2/post/11906d6d-4fc7-46a0-9645-1b225fe228a3/image.png" width="60%" height="30%"> Posterior distribution : 주어진 데이터로 학습할 때 parameters 의 확률 분포 ${\rightarrow}$ 모델링이 어렵다. ${\Rightarrow}$ true posterior 사이의 KL divergence 를 최소화하는 variatoinal distribution 을 찾는 것 ## 01. ABSTRACT > VAE 를 implicit feedback 에 대한 collaborative filtering 으로 확장한다. - Non-linear probabilistic model 사용으로 성능 개선 - Multinomial likelihood 사용 - Parameter estimation 에서 bayesian inference 사용 - maximum entropy discrimination 과 information bottleneck principle 사용 - maximum entropy discrimination : 주어진 입력에 대해 가장 가능성이 높은 클래스를 결정하기 위해 maximum entropy theory 를 사용하는 분류 방법 - information bottleneck principle : Noise 를 최소화하면서 data set 과 가장 연관성이 높은 정보를 추출하는 방법 ## 02. Introduction > 추천 시스템에서 다루는 데이터 셋은 user 와 아주 적은 item 간의 상호 작용만 있기 때문에, small data set problem 이라고 주장한다. - VAE 는 linear-factor model 을 생성하고 non-linear probabilistic latent-variable model 을 제안한다. - User 로 부터 sparse 한 signal 들 만 사용하고 overfitting 을 피하기 위해 user 와 item 사이의 통계적 강점을 공유하는 probabilistic latent-variable model 을 사용한다. - principled-bayesian approach 를 사용하여 data 의 scarcity 와 관계없이 robust 한 성능을 보인다. ## 03. Model > 해당 논문에서 generative process 는 deep latent Gaussian model 과 유사하다. - 각각의 사용자 ${u}$ 에 대해, 표준 Gaussian prior 로 부터 K 차원 latent representation ${z_u}$ 를 sampling 함으로써 시작한다. - Sampling 된 ${z_u}$ 는 non-linear function ( ${f_{\theta}(\cdot) \in \R^I}$ ) 에 의해 변형된다. - non-linear function ${f_{\theta}(\cdot)}$ 은 parameter ${\theta}$ 를 가지는 multilayer perceptron 이다. - ${z_u}$ 에 non-linear functoin 을 적용한 결과는 확률 vector ${\pi(z_u) \in S^{I-1}}$ 이다. ${\rightarrow}$ 해당 generative model 은 latent-factor model 을 일반화한다. `참고` ${f_{\theta}(\cdot)}$ 를 linear 한 함수로 두고 Gaussian likelihood 를 사용하면 classical matrix factorization 을 recover 할 수 있다. 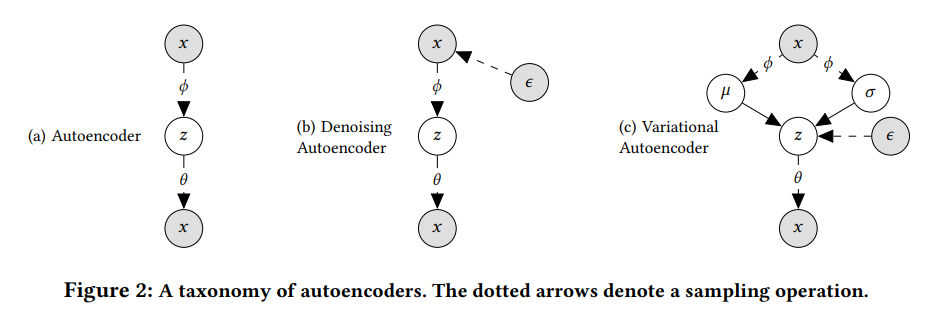--- ![](https://velog.velcdn.com/images/hobbang2/post/9c581616-3e60-4fb6-95db-25fbbc95c013/image.png) ( b ) DAE : ${x}$ 에 noise ${\epsilon}$ 을 추가하여 복원 ( c ) VAE : ${x}$ 를 encoder ${g_{\phi}(\cdot)}$ 를 이용해 평균 ${\mu}$ 와 분산 ${\sigma}$ 를 구한다. 구해진 평균과 분산으로 K-차원 latent representation ${z}$ 를 샘플링한다. ${z}$ 를 다시 decoder ${f_{\theta}}$ 로 복원한다. --- ## 04. Experimental setup - training / validation / test sets 로 나누어 학습한다. - training user 에 대한 전체 click history 를 사용한다. 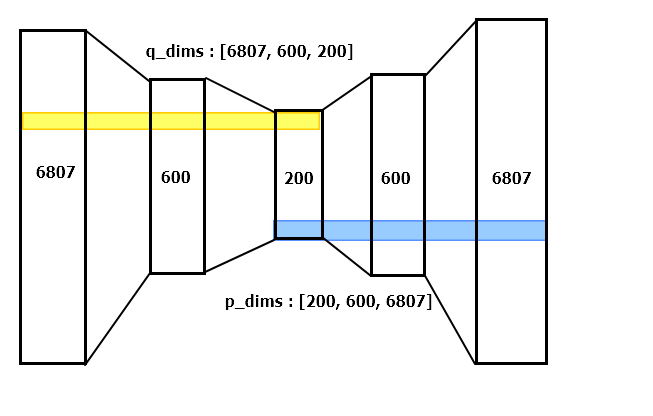- 1 ( 또는 0 ) 개의 hidden layer 를 가지는 Multi-VAE / Multi-DAE 구조가 가장 좋은 성능을 냈다. ${( [ I \rightarrow 600 \rightarrow 200\rightarrow 600 \rightarrow I ] ) }$ - layer 간의 activation function 으로 tanh 을 사용했다. - Mult-VAE 에서 ${g_\phi(\cdot)}$ 의 결과는 Gaussian random variable 의 평균 ( mean ) ${\mu}$ 와 분산 ( variance ) ${\sigma}$ 로 사용되기 때문에 activation function 을 사용하지 않는다. - hidden layter 가 0 개 인 경우 log-linear model 이다. - anneal KL term 으로 성능 향상 ( 찾아보기 ! ) - Drop out 은 input layer 에 대해 모두 0.5 - VAE model 에는 weight decay 사용하지 않는다. - mult-VAE 와 Mult-DAE 모두 500 명의 user 를 가지는 batch 에서 Adam optimizer 사용 > 🐬 `checkpoint` > - ${P_{data}}$ 에서 smapling 된 ${x}$ > - 　Input ${x}$ 의 평균 ${\mu}$ 와 분산 ${\sigma}$ 로 부터 ${z}$ 를 sampling 한다. 　 > - ${\mu}$ 에 따라서 distribution 의 어디에 위치하는지 등에 대한 정보가 결정된다. > - ${\rightarrow}$ linear layer 는 ${\mu}$ 와 ${logvar}$ 에 대한 확률적인 값을 뽑기 위한 것 > - ${\mu}$ 와 ${logvar}$ 가 고정되면 값이 고정된다. ${\rightarrow}$ 항상 동일한 분포에서 sampling 된다. > - 따라서, ${\mu}$ 와 ${logvar}$ 에 대한 linear layer 로 input 에 따른 ${\mu}$ 와 ${variance}$ 값을 뱉는다. > > ${\Rightarrow}$sampling function 에 들어가는 mu 와 variance 의 값이 됨 ## 05. Code ![](https://velog.velcdn.com/images/hobbang2/post/ce4ede0a-d26d-4149-9afa-8cb2cccefe50/image.png) ### 1 ) MultiDAE ```python class MultiDAE(nn.Module): """ Container module for Multi-DAE. Multi-DAE : Denoising Autoencoder with Multinomial Likelihood See Variational Autoencoders for Collaborative Filtering https://arxiv.org/abs/1802.05814 """ def __init__(self, p_dims, q_dims=None, dropout=0.5): super(MultiDAE, self).__init__() self.p_dims = p_dims # [200, 600, 6807] if q_dims: assert q_dims[0] == p_dims[-1], "In and Out dimensions must equal to each other" assert q_dims[-1] == p_dims[0], "Latent dimension for p- and q- network mismatches." self.q_dims = q_dims else: self.q_dims = p_dims[::-1] # [6807, 600, 200] self.dims = self.q_dims + self.p_dims[1:] # [6807, 600, 200] + [600, 6807] self.layers = nn.ModuleList([nn.Linear(d_in, d_out) for d_in, d_out in zip(self.dims[:-1], self.dims[1:])]) # ( [6807, 600, 200, 600] , [600, 200, 600, 6807] ) self.drop = nn.Dropout(dropout) self.init_weights() def forward(self, input): # normal distribution 을 따르지 않은 input 에 대해 편향을 줄여줌 # 예 ) 평점을 대체로 높게 주는 사용자와 낮게 주는 사용자의 편향을 줄임 h = F.normalize(input) h = self.drop(h) for i, layer in enumerate(self.layers): h = layer(h) if i != len(self.weights) - 1: h = F.tanh(h) return h def init_weights(self): for layer in self.layers: # Xavier Initialization for weights size = layer.weight.size() fan_out = size[0] fan_in = size[1] std = np.sqrt(2.0/(fan_in + fan_out)) layer.weight.data.normal_(0.0, std) # Normal Initialization for Biases layer.bias.data.normal_(0.0, 0.001) ``` ### 2 ) MultiVAE ```python class MultiVAE(nn.Module): """ Container module for Multi-VAE. Multi-VAE : Variational Autoencoder with Multinomial Likelihood See Variational Autoencoders for Collaborative Filtering https://arxiv.org/abs/1802.05814 """ def __init__(self, p_dims, q_dims=None, dropout=0.5): super(MultiVAE, self).__init__() self.p_dims = p_dims if q_dims: assert q_dims[0] == p_dims[-1], "In and Out dimensions must equal to each other" assert q_dims[-1] == p_dims[0], "Latent dimension for p- and q- network mismatches." self.q_dims = q_dims else: self.q_dims = p_dims[::-1] # Last dimension of q- network is for mean and variance temp_q_dims = self.q_dims[:-1] + [self.q_dims[-1] * 2] self.q_layers = nn.ModuleList([nn.Linear(d_in, d_out) for d_in, d_out in zip(temp_q_dims[:-1], temp_q_dims[1:])]) self.p_layers = nn.ModuleList([nn.Linear(d_in, d_out) for d_in, d_out in zip(self.p_dims[:-1], self.p_dims[1:])]) self.drop = nn.Dropout(dropout) self.init_weights() # Gaussian Distribution def forward(self, input): mu, logvar = self.encode(input) z = self.reparameterize(mu, logvar) return self.decode(z), mu, logvar def encode(self, input): # normal distribution 을 따르지 않은 input 에 대해 편향을 줄여줌 # 예 ) 평점을 대체로 높게 주는 사용자와 낮게 주는 사용자의 편향을 줄임 h = F.normalize(input) h = self.drop(h) for i, layer in enumerate(self.q_layers): h = layer(h) if i != len(self.q_layers) - 1: h = F.tanh(h) else: # z 값을 sampling 할 multinomial distributio 의 평균과 logvar mu = h[:, :self.q_dims[-1]] logvar = h[:, self.q_dims[-1]:] return mu, logvar def reparameterize(self, mu, logvar): if self.training: # Gaussian 분포의 표준 편차를 구하는 식 ( 분산의 제곱근 ) std = torch.exp(0.5 * logvar) eps = torch.randn_like(std) return eps.mul(std).add_(mu) else: return mu def decode(self, z): h = z for i, layer in enumerate(self.p_layers): h = layer(h) if i != len(self.p_layers) - 1: h = F.tanh(h) return h def init_weights(self): for layer in self.q_layers: # Xavier Initialization for weights size = layer.weight.size() fan_out = size[0] fan_in = size[1] std = np.sqrt(2.0/(fan_in + fan_out)) layer.weight.data.normal_(0.0, std) # Normal Initialization for Biases layer.bias.data.normal_(0.0, 0.001) for layer in self.p_layers: # Xavier Initialization for weights size = layer.weight.size() fan_out = size[0] fan_in = size[1] std = np.sqrt(2.0/(fan_in + fan_out)) layer.weight.data.normal_(0.0, std) # Normal Initialization for Biases layer.bias.data.normal_(0.0, 0.001) def loss_function(recon_x, x, mu, logvar, anneal=1.0): # BCE = F.binary_cross_entropy(recon_x, x) BCE = -torch.mean(torch.sum(F.log_softmax(recon_x, 1) * x, -1)) KLD = -0.5 * torch.mean(torch.sum(1 + logvar - mu.pow(2) - logvar.exp(), dim=1)) return BCE + anneal * KLD ```