# Why?

Improve Model Performance: 原始數據通常包含噪聲、不完整或不相關的資訊。特徵工程可以提取重要的資訊，降低噪聲，從而提高模型的準確性和性能。

Address Data Quality Issues: 資料集可能包含缺失值(Missing Values)、異常值(outliers)或不一致的數據(inconsistent data)。通過特徵工程，可以清理和準備資料，使其適合用於模型訓練。

Dimensionality Reduction: 高維度數據集容易導致模型過擬合，因為模型可能會學習到數據中的噪聲。特徵工程通過選擇最重要的特徵或進行降維(dimensionality reduction)，降低模型的複雜度，防止過擬合。

Increase Model Interpretability: 原始特徵並不直觀或難以解釋。通過創建新特徵或轉換現有特徵，可以使模型的輸出更具解釋性，便於理解和分析。

# Managing Categorical Data

Model Requirements : 許多機器學習算法（如線性回歸、支持向量機）只能處理數值數據，因此需要將分類數據轉換為數值形式

Improving Model Performance : 正確處理分類數據可以提高模型的性能和準確性。

Handling Sparsity : 高基數的分類數據會導致稀疏性問題，增加計算複雜度。

### Methods :
標籤編碼（Label Encoding）:
將每個類別標籤轉換為唯一的一個數字。例如，將“紅色”、“藍色”和“綠色”分別編碼為0、1和2。

獨熱編碼（One-Hot Encoding）:
將每個類別標籤轉換為二進制向量。每個類別都有自己的位元，並在該位元上設置為1，其餘設置為0。例如，“紅色”編碼為[1, 0, 0]，“藍色”編碼為[0, 1, 0]，“綠色”編碼為[0, 0, 1]。

頻率編碼（Frequency Encoding）：
將每個類別標籤替換為該類別在數據集中出現的頻率。例如，如果“紅色”出現的頻率為0.5，“藍色”為0.3，“綠色”為0.2，則分別編碼為0.5、0.3和0.2。

目標編碼（Target Encoding）：
將每個類別標籤替換為該類別在目標變量上的平均值。例如，如果分類特徵是“城市”，目標變量是“收入”，則用每個城市對應的平均收入替換城市名稱。

Python : LabelEncoder、直接用dataframe的replace取代

# Managing Missing Features

### Methods :

**移除整行數據(Removing the whole line)**:

資料集相當大：如果資料集中有數十萬或數百萬條記錄，移除幾千行不會對資料的整體代表性造成重大影響。
缺失特徵的數量較多：當資料集中某些特徵缺失的比例很高時，這些特徵的預測會變得非常困難且不準確。
任何預測都有風險：如果缺失值的特徵對模型的預測結果有很大影響，而預測這些特徵的誤差又會嚴重影響最終的結果，則應該避免進行預測。

**創建子模型來預測那些特徵(Creating sub-model to predict those features)**：

創建子模型：這意味著我們需要為每一個缺失的特徵建立一個單獨的預測模型。
監督學習策略：這涉及到為每個模型選擇合適的算法、確定模型的輸入（特徵）和輸出（目標），並使用已有的數據來訓練這些模型。
預測缺失值：訓練好的模型將用來預測那些原本缺失的特徵值。

ex:
假設我們有一個數據集，包含以下特徵：年齡、收入、教育程度和工作年限。現在有些記錄中“收入”這個特徵是缺失的。

創建子模型來預測“收入”：

我們可以使用“年齡”、“教育程度”和“工作年限”這些已知特徵來預測“收入”。
為此，我們需要選擇一個合適的算法（如線性回歸、決策樹等），並用已經有“收入”數據的部分來訓練這個模型。
訓練完成後，我們可以使用這個模型來預測那些“收入”缺失的記錄中的收入值。

**使用自動策略根據其他已知值來填補缺失值(Using an automatic strategy to input them according to the other known values**):

* 平均值（Mean）：
使用該特徵的所有非缺失值的平均值來填補缺失值。
適合於數據分佈相對均勻且沒有極端值的情況。
* 中位數（Median）：
使用該特徵的所有非缺失值的中位數來填補缺失值。
適合於數據分佈有偏或有極端值的情況。
* 頻率（Frequency，也稱為眾數）：
使用該特徵中最常出現的值來填補缺失值。
適合於分類特徵或有一個值出現頻率很高的情況

# Data Scaling and Normalization

**Normalization（正規化）**
使用時機：

當特徵有不同的量級：例如，當特徵的值範圍相差很大時，如房屋價格（數萬到數十萬）和房屋面積（幾十到幾百）。
需要確保數據在特定範圍內：一些機器學習算法（如神經網絡、K-最近鄰算法）對特徵的尺度敏感，數據範圍應該被限定在一個特定的區間內。

[10, 20, 30, 40, 50]
Min-Max normalization
x=10, 10-10/50-10 = 0
x=20, 20-10/50-10 = 0.25
x=30, 30-10/50-10 = 0.5
x=40, 40-10/50-10 = 0.75
x=50, 50-10/50-10 = 1

[0, 0.25, 0.5, 0.75, 1]

**Standardization（標準化）**
使用時機：

當特徵服從高斯分佈：如果數據的分佈近似於高斯分佈（鐘形曲線），標準化可以使數據的特徵在相同的尺度上。
對於大多數機器學習算法：很多算法假設數據是標準化的，例如線性回歸、邏輯回歸、線性判別分析（LDA）、支持向量機（SVM）和K均值聚類。

**Standardization還可以使離群值(outlier)對整個model的影響大大減低。**

Z-score standardization
μ= (10+20+30+40+50)/5=30
σ= [((10-30)^2^+(20-30)^2^+(30-30)^2^+(40-30)^2^+(50-30)^2^)/5]^-1^ = [(400+100+0+100+400)/5]^-1^= 14.14
x=10, 10-30/14.14 = −1.41
x=20, 20-30/14.14 = −0.71
x=30, 30-30/14.14 = 0
x=40, 40-30/14.14 = 0.71
x=50, 50-30/14.14 = 1.41

[-1.41, -0.71, 0, 0.71, 1.41]

**Regularization（正則化）**
使用時機：

防止過擬合：當模型過於複雜（如參數過多）且在訓練數據上表現良好但在測試數據上表現較差時，正則化可以減少模型的複雜度，提高模型的泛化能力。
高維數據集：當特徵數量比樣本數量多時，正則化有助於防止過擬合，特別是在基於迭代優化的模型中。

**L1 正則化（Lasso Regularization）**

Loss=Original Loss+λ∑∣wi∣

特性：

可以讓某些權重變成 0

適合用來做 特徵選擇（Feature Selection）

**L2 正則化（Ridge Regularization）**

Loss=Original Loss+λ∑wi^2^

特性：

不會讓權重變 0，但會讓權重變小（收斂到接近 0）

適合所有特徵都重要時

**Elastic Net 正則化**

Loss=Original Loss+λ1∑∣wi∣+λ2∑wi^2^

# Feature selection and dimension reduction

**Low Variance Filter** :
在資料集中，如果某個變量的所有觀察值都相同，這個變量對模型的貢獻將會非常有限。這是因為該變量沒有變異性，對模型來說沒有提供有價值的資訊。在實務中，我們需要計算每個變量的方差，並且刪除那些方差很低的變量。以下是詳細的解釋與例子：

為什麼零方差變量無法改進模型
缺乏資訊：如果一個變量的所有值都相同，比如說都是1，那麼這個變量就沒有變異性。對於模型來說，這樣的變量無法幫助區分數據的不同部分。舉個例子，假設我們用這個變量來預測房價，但所有的值都是1，那麼無論其他特徵如何變化，這個變量都無法提供任何額外的資訊來幫助預測房價。

零方差：方差是衡量資料分佈程度的一個指標。如果一個變量的所有值都相同，則其方差為零。方差為零意味著這個變量在資料集中沒有任何變化，對模型的影響為零。

**High Correlation Filter** :
高相關性意味著兩個變量之間有相似的趨勢和資訊。在一些模型中，這種高相關性可能會導致模型性能的下降，特別是對於線性回歸和邏輯回歸模型。通常，如果一對變量的相關性大於0.5-0.6，我們應該認真考慮刪除其中一個變量。

多重共線性：在線性回歸和邏輯回歸模型中，高度相關的變量會引入多重共線性問題，這會導致模型係數的不穩定，進而影響模型的解釋能力和預測準確性。

冗餘資訊：高度相關的變量通常攜帶相似的資訊，這會增加模型的計算負擔，而不會提供額外的有價值的資訊。這種冗餘會使模型變得複雜，降低泛化能力。

**Feature Importance Filter** :

Filter 方法（過濾法）
皮爾森相關係數（Pearson Correlation）：計算特徵與目標的線性相關。
卡方檢定（Chi-Square Test）：適用於分類問題，衡量特徵與目標變數的關聯。
互資訊（Mutual Information）：衡量特徵與目標變數的資訊共享程度，適用於非線性關係。
方差閾值（Variance Threshold）：剔除變異性太低的特徵（幾乎是常數的欄位）。

Wrapper 方法（包裝法）
遞迴特徵消除（Recursive Feature Elimination, RFE）：從所有特徵開始，逐步移除重要性最低的特徵。
前向選擇（Forward Selection）：從空集合開始，逐步加入能提升模型表現的特徵。
後向剃除（Backward Elimination）：從全特徵開始，逐步移除對模型貢獻最小的特徵。
遺傳演算法、貪婪演算法：用於搜尋最佳特徵子集。

Embedded 方法（嵌入法）
Lasso Regression（L1 正則化）：會自動將部分權重推為 0，達到特徵選擇的效果。
Decision Tree / Random Forest / XGBoost 特徵重要性：這類模型內建 feature importance 評估方式。
Elastic Net：結合 L1 和 L2 正則化，能在稀疏性與穩定性之間取得平衡。

SHAP / LIME
雖然本質是 模型可解釋性工具，但它們可以幫助你：
判斷「哪些特徵」對模型預測最有影響。
基於這些貢獻值，你可以進行特徵選擇（例如：只保留 SHAP 值貢獻高的特徵）。
✅ 算是特徵選擇的輔助工具，實務中常配合用來做選擇。

**Principal component analysis** :

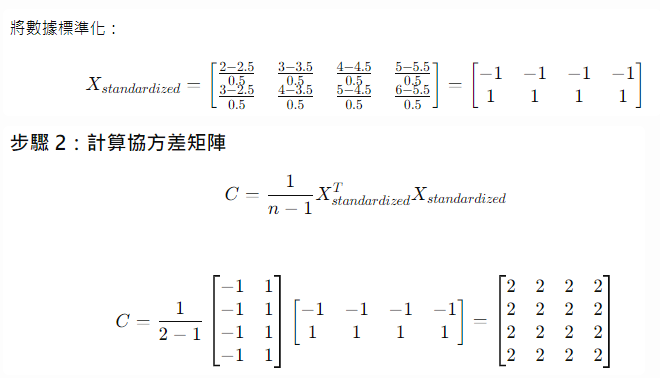
1.標準化數據 (Data standardization)
2.計算協方差矩陣 (Correlation matrix)
3.計算協方差矩陣的特徵值和特徵向量 (Eigenvalues & Eigenvectors)
4.構造投影矩陣 (Construct the projection matrix )
5.轉換數據到新的特徵子空間 (Transform new feature subspace )


Feature Cleaning (特徵清理)
* 缺失值處理 (填補、中位數、平均數、刪除)
* 移除異常值 (Outlier Removal)
* 修正錯誤值、重複值
* 標準化或正規化 (Normalizing/Standardizing)

Feature Transformation (特徵轉換)
* 類別編碼 (Categorical Encoding)
* 數值變換 (Numerical Transformation)
* 特徵構建 (Feature Construction / Extraction)
* 維度縮減 (Dimensionality Reduction)

Feature Selection (特徵選擇)
* Filter Methods (篩選法)
* Wrapper Methods (包裝法)
* Embedded Methods (嵌入法)

順序的重要性：
若 Feature Cleaning 做得不完整，後續步驟會受到干擾，可能導致模型效能低下。
Feature Transformation 應該在 Feature Selection 之前，否則模型無法充分學習轉換後的特徵。
不遵循順序可能會使不相關特徵殘留，影響模型準確度。