# **Supervised Learning(有label)**

有input x的資料(age,balance,loan)
有output y的資料(labels,targets)

經過training後，試圖從x找出的^y能夠越接近y越好(兩者的距離稱之為loss)

**Regression** 是指Continuous values : stock price, house price
**Clssification** 是指 discrete values : email message spam or not, an image of a dog

# **Unsupervised Learning(無label)**

根據資料之間的相似性(similarity or distance measure)，將資料分群

Goal: **internal coherence**, **separation among clusters**

# The ML Mindset
> Step Example
> 1.Set the research goal. | I want to predict how heavy traffic will be on a given day.
> 2.Make a hypothesis. | I think the weather forecast is an informative signal.
> 3.Collect the data. | Collect historical traffic data and weather on each day.
> 4.Test your hypothesis. | Train a model using this data.
> 5.Analyze your results. | Is this model better than existing systems?
> 6.Reach a conclusion. | I should (not) use this model to make predictions, because of X, Y, and Z.
> 7.Refine hypothesis and repeat. | Time of year could be a helpful signal.

# About Data

We expect all samples to be independent and identically distributed (i.i.d)

**Binary classification** : classifying instances into one of the two classes. (ex. spam/not spam)
**Multiclass classification** : the problem of classifiying instances into one of three or more classes. (ex. red/black/white/green)

### Multiclass Strategies
**One-vs-one**:

training a model for each pair of classes.
假設有 5 個類別（A, B, C, D, E），需要訓練c5取2=10個二元分類器:

> 1. A vs. B
> 2. A vs. C
> 3. A vs. D
> 4. A vs. E
> 5. B vs. C
> 6. B vs. D
> 7. B vs. E
> 8. C vs. D
> 9. C vs. E
> 10. D vs. E

假設我們有一個新樣本 x，並且我們使用上述 10 個分類器進行預測：

A vs. B：預測為 A，A 得 1 票。
A vs. C：預測為 C，C 得 1 票。
A vs. D：預測為 A，A 得 1 票。
A vs. E：預測為 E，E 得 1 票。
B vs. C：預測為 C，C 得 1 票。
B vs. D：預測為 D，D 得 1 票。
B vs. E：預測為 E，E 得 1 票。
C vs. D：預測為 D，D 得 1 票。
C vs. E：預測為 E，E 得 1 票。
D vs. E：預測為 D，D 得 1 票。

統計投票結果：

A 得 2 票
B 得 0 票
C 得 2 票
D 得 3 票
E 得 3 票
在這個例子中，類別 D 和 E 得到最多票數（3 票），我們可能需要進行進一步的決策來選擇最終類別，或者通過其他方法來解決平票問題。

**One-vs-all**:

同樣例子

假設有 5 個類別（A, B, C, D, E），需要訓練5個二元分類器:
A vs. {B, C, D, E}
B vs. {A, C, D, E}
C vs. {A, B, D, E}
D vs. {A, B, C, E}
E vs. {A, B, C, D}

假設我們有一個新樣本 x，並且我們使用上述 5 個分類器進行預測：

A vs. Others：預測概率 0.2
B vs. Others：預測概率 0.1
C vs. Others：預測概率 0.4
D vs. Others：預測概率 0.15
E vs. Others：預測概率 0.25
在這個例子中，類別 C 的預測概率最高（0.4），因此最終預測結果是類別 C。

**One-vs-one**:

Pros:
分類器簡單：每個二元分類器只需區分兩個類別，問題相對簡單。
適合平衡類別：每個分類器在訓練時只需關注兩個類別，不受其他類別的影響，適合類別數量均衡的情況。
較好的性能：在某些情況下，OvO 方法可以提高分類器的性能，因為每個分類器專注於特定的類別對。
Cons:
分類器數量多：需要訓練和預測較多的分類器，計算量大。對於 k 個類別，需要k(k-1)/2個分類器
投票機制複雜：預測時需要統計每個分類器的投票結果，增加了預測過程的複雜度。
適用性有限：對於類別數量非常多的情況，訓練和預測的時間成本會顯著增加。

適用情況：

類別數量相對較少（例如 k≤10）。
類別間存在較強的區分特徵。
計算資源充足，可以承受較高的訓練和預測時間。

**One-vs-all**:

Pros:
分類器數量少：只需訓練和預測 k 個分類器，計算量相對較小。
簡單直接：每個分類器將一個類別與其他所有類別區分，實現簡單直接。
訓練高效：訓練和預測過程更高效，適合大規模數據集。
Cons:
不平衡問題：當類別不平衡時（例如某些類別樣本數遠多於其他類別），分類器的性能可能受到影響。
分類器複雜：每個分類器需要處理多個類別之間的區分，問題相對複雜。
適用性有限：在某些情況下，可能無法有效處理類別之間的細微差異。

適用情況：

類別數量相對較多（例如 k>10）。
類別之間區分特徵不夠明顯。
計算資源有限，需要高效的訓練和預測。

# Bias-Variance Trade-off

偏差誤差（Bias Error）：由模型的簡化假設引起的誤差。
方差誤差（Variance Error）：由訓練數據的變動引起的誤差。
噪聲（Noise）：數據本身不可避免的隨機誤差，無法通過模型改進來減少。

為什麼是這三種因素?
Bias:偏差反映了模型的學習能力和假設與真實樣本之間的差異
Variance:方差反映了模型對訓練數據的敏感度，即模型能否適應不同的訓練集
Noise:噪聲反映了數據中的隨機誤差和不可預測的因素，這些誤差來源於數據本身

泛化:指訓練後的模型能不能夠很好的將學習過的知識應用到未見過的數據上，並做出準確預測的能力

總體誤差公式為：
Expected Error=Bias^2+Variance+Irreducible Error (Noise)

**偏差誤差（Bias Error）**:

偏差誤差通常出現在模型過於簡單，無法捕捉數據中的複雜模式的情況下。例如，使用線性回歸來擬合非線性數據。
這樣的模型對數據的假設過於簡單，認為數據可以用簡單的模式來表示，結果是它無法正確地反映數據的真實特徵。

對訓練數據和測試數據的影響：

高偏差的模型在訓練數據和測試數據上都會表現不佳，因為它無法正確捕捉數據的真實模式，導致高誤差。
例如，如果我們用一條直線來擬合明顯的二次曲線數據，我們會看到模型的預測偏差很大，無法與真實數據匹配。

結果：

模型表現欠佳，無法準確預測，即所謂的“欠擬合”**（Underfitting）**。
偏差誤差高，因為模型不能很好地擬合訓練數據中的模式。

**方差誤差（Variance Error）**:

方差誤差通常出現在模型過於複雜，對訓練數據中的噪聲進行了過度擬合的情況下。例如，使用高次多項式回歸來擬合線性數據。
這樣的模型對訓練數據中的每一個變動都非常敏感，包括噪聲，結果是它過度擬合了訓練數據。

對訓練數據和測試數據的影響：

高方差的模型在訓練數據上會表現得非常好（誤差很低），但在測試數據上表現不佳（誤差很高），因為它過度擬合了訓練數據中的噪聲，無法很好地泛化到新數據。
例如，如果我們用一條過於複雜的曲線來擬合簡單的線性數據，模型在訓練數據上可能預測得非常準確，但在新數據上誤差會很大。
結果：

模型表現過擬合 **（Overfitting）** ，即對訓練數據過度擬合，對測試數據泛化能力差。
方差誤差高，因為模型對訓練數據中的噪聲進行了過度擬合。

# 為什麼無法同時找到低Bias和低Variance的model?
假設今天一筆資料的分布如下:
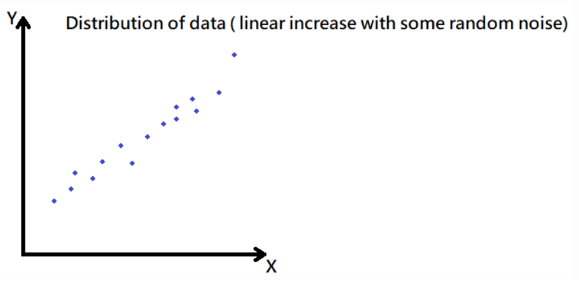
用肉眼很直觀的可以發現資料似乎是呈現一種線性分布，不過還是有一些噪聲在裡面
如果使用一個非常簡單的數學模型 Y=ax+b去盡可能的擬合這些資料，如下:
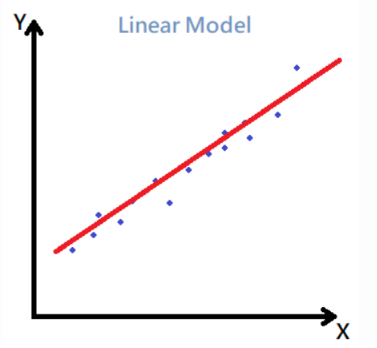
如果使用複雜的數學模型 Y=a0+a1x+a2x^2^+a3x^3^+ ... +anx^n 時，如下:

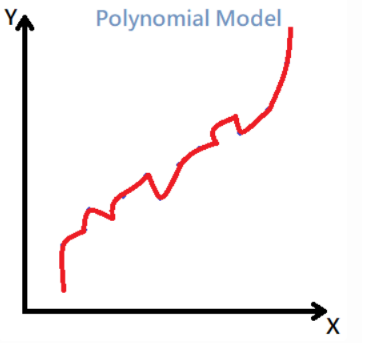
可以發現簡單的數學模型相比複雜的模型Bias要來得高，當使用複雜數學的模型將每一條點連成奇形怪狀的線
這樣你發現模型的Bias可就變成0了!

但是我們最終的目的是希望拿這個模型去對未知的資料進行預測，所以當拿一筆全新的資料進行預測時
就會發現用N次多項式模型所做出來的預測，答案錯的有夠離譜，反而線性模型做出來的預測會比較接近真實答案。

會造成這樣的原因是因為，我們一開始就太希望把Bias降到0，所以建立了一個非常複雜的數學模型，讓模型可以把所有訓練過的資料都記憶下來。

這樣做有一個很大的問題就是，資料裡面其實是帶有很多隨機誤差的，當我們把這些誤差全部訓練進去模型裡面，會容易導致你的模型失去泛化的能力。
也就是**Overfitting**


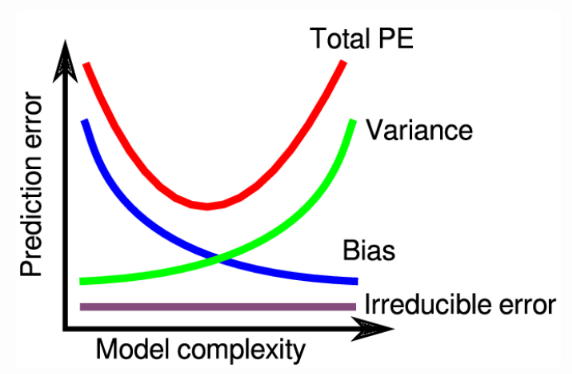
由於偏差和方差之間存在此種權衡，實際應用中，我們的目標是找到一個最佳平衡點，使得總誤差最小化。這通常涉及以下步驟：

> 選擇適當的模型複雜度：
> 初期模型可能過於簡單，導致高偏差（欠擬合）。
> 隨著模型複雜度增加，偏差誤差會減少，但方差誤差會增加。
>
> 交叉驗證：
> 使用交叉驗證技術來評估模型在不同複雜度下的性能，以找到最佳的平衡點。
>
> 正則化技術：
> 使用正則化（如Lasso和Ridge回歸）來控制模型的複雜度，減少過擬合。