假設腫瘤（tumors）的資料如下：
Total: 100
Total positive: 9 (9%)
Total negative: 91 (91%)

在不平衡數據集中，僅僅依賴準確率（accuracy）來評估模型性能是不夠精確的

偏向多數類別：

在不平衡數據集中，多數類別樣本數遠多於少數類別。由於模型在訓練過程中接觸到的多數類別樣本更多，它更有可能傾向於預測多數類別。這樣，即使模型大部分時間都預測為多數類別，也會有很高的準確率。
例如，在例子中，假設模型總是預測“沒有腫瘤”，那麼模型的準確率會是91%，但這個模型對於檢測腫瘤的病人（正類別）的能力非常差。

忽略少數類別的性能：
高準確率可能掩蓋了模型對少數類別（如腫瘤病人）的差勁表現。由於少數類別樣本數少，模型即使預測錯誤，也不會顯著影響整體準確率，但這種錯誤對實際應用影響很大，特別是在醫療診斷中。

模型效果的錯誤認知：
僅看準確率，容易對模型的實際效果產生錯誤認知，導致模型在應用中表現不佳，特別是當我們更關心少數類別的預測時。

EX:
實際類別 預測類別 數量
Positive Positive 1
Positive Negative 8
Negative Positive 0
Negative Negative 91

準確率：模型預測的準確率是92%，這看起來非常高，給人一種模型表現良好的錯覺。
精確率：模型對於預測為正類（腫瘤）的樣本中，實際為正類的比例是100%，因為模型只預測了1個腫瘤，且這個預測是正確的。
召回率：模型對於實際為正類（腫瘤）的樣本中，僅正確預測了11.1%，這表示模型對於腫瘤的檢測能力非常差。

實際應用影響
在醫療診斷中，如果模型不能有效地檢測出腫瘤患者（即召回率低），那麼即使模型的整體準確率很高，這個模型在實際應用中仍然是不可靠的。漏診的腫瘤患者（8個漏診的樣本）可能會錯過及時治療的機會，對病人健康造成嚴重影響

# Change Classification Metrics

𝑃_𝑜𝑏𝑠𝑒𝑟𝑣𝑒𝑑: Probability of observed agreement (ie. the overall accuracy of the model)
𝑃_𝑏𝑦𝑐ℎ𝑎𝑛𝑐𝑒: Probability of agreement by chance (ie. the measure of the agreement between the model predictions and the actual class values as if happening by chance)

Kappa coefficient：
𝜅=(𝑃_𝑜𝑏𝑠𝑒𝑟𝑣𝑒𝑑−𝑃_𝑏𝑦𝑐ℎ𝑎𝑛𝑐𝑒)/(1−𝑃_𝑏𝑦𝑐ℎ𝑎𝑛𝑐𝑒 )

Ex:

TP:1 FP:1
FN:8 TN:90
Total=100

TP:1/100=0.01
TN:90/100=0.9
FN:8/100=0.08
FP:1/100=0.01

𝑃_𝑜𝑏𝑠𝑒𝑟𝑣𝑒𝑑= 0.01 + 0.9 = 0.91
𝑃_𝑏𝑦𝑐ℎ𝑎𝑛𝑐𝑒= 0.02(TP+FP) * 0.09(TP+FN) + 0.98(FN+TN) * 0.91(FP+TN) = 0.8936

𝜅=(𝑃_𝑜𝑏𝑠𝑒𝑟𝑣𝑒𝑑−𝑃_𝑏𝑦𝑐ℎ𝑎𝑛𝑐𝑒)/(1−𝑃_𝑏𝑦𝑐ℎ𝑎𝑛𝑐𝑒 )
= (0.91 −0.8936)/(1 −0.8936)
= 0.0164/0.1064=15.41%

Kappa系數（κ）用於衡量分類模型的預測結果和實際觀察結果之間的一致性，其值範圍通常在[−1,1] 之間。Kappa系數越接近1，表示模型預測結果和實際觀察結果的一致性越高，即模型效果越好
若資料集越 balanced， 𝜅 的值越大

# Resampling Dataset

**Over-sampling**

sampling with replacement :
把樣本從母體抽樣出來之後，再放回母體給下次的抽樣。意思就是同一筆資料可能出現多次。

SMOTE :
該算法通過選擇兩個或多個相似的樣本（使用距離度量）來生成合成樣本，並在不同屬性上通過隨機數量的擾動來產生新的樣本。如何選擇鄰居以及計算距離是改進這種算法的新方向。

1.選擇少數類別樣本：從少數類別中選擇一個樣本𝑥𝑖。
2.尋找鄰居：在少數類別中使用距離度量（如歐幾里得距離）找到該樣本的k個最近鄰居。
3.生成合成樣本：對於每個選定的鄰居樣本𝑥𝑖,𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑟，生成一個合成樣本。具體步驟如下：
* 對於樣本的每個屬性，計算兩個樣本間的差異。
* 將這個差異乘以一個介於0和1之間的隨機數，再加上原樣本的屬性值。
* 這樣，每個屬性就被隨機擾動了一個值，產生了一個新的合成樣本。

假設我們有一個少數類別樣本𝑥𝑖和它的鄰居𝑥𝑖,𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑟，它們在兩個特徵空間中的表示如下：
𝑥𝑖=(2,3)
𝑥𝑖,𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑟=(4,7)
為生成一個合成樣本，我們可以按以下步驟進行：

計算每個屬性的差異：
差異 =𝑥𝑖,𝑛𝑒𝑖𝑔ℎ𝑏𝑜𝑟−𝑥𝑖=(4−2,7−3)=(2,4)

對每個屬性乘以一個隨機數（假設為 0.5）：

擾動值 =(2∗0.5,4∗0.5)=(1,2)

將擾動值加到原樣本上：
新的合成樣本 =𝑥𝑖+擾動值=(2+1,3+2)=(3,5)=x

因此，新的合成樣本為 (3,5)。

選擇鄰居和計算距離是改進SMOTE算法的關鍵方向

1.距離度量的選擇：
歐幾里得距離：最常用的距離度量，但對於高維數據和非線性數據效果較差。
曼哈頓距離：對於一些特定的數據分佈可能更有效。
馬氏距離：考慮了數據分佈的共變異數矩陣，對高維數據更穩定。
余弦相似度：適用於文本數據等高維稀疏數據。

2.鄰居選擇的策略：
隨機選擇：傳統SMOTE中隨機選擇k個鄰居，但可能包含噪聲數據。
聚類選擇：通過聚類方法（如KMeans）選擇同一聚類中的鄰居，減少噪聲影響。
加權選擇：根據樣本的重要性或相似性給予鄰居不同的權重。

**Under-sampling**

範例程式碼:

import random
import numpy as np
import pandas as pd
from imblearn.over_sampling import RandomOverSampler, SMOTE
from imblearn.under_sampling import RandomUnderSampler
from collections import Counter
import seaborn as sns
import matplotlib.pyplot as plt

# 設定隨機種子，使每次產生的資料相同
random.seed(2022)
np.random.seed(2022)

n1 = 200  # 第一類的數量(type1)
n2 = 20   # 第二類的數量(type2)

# 產生type1的data
x = np.random.normal(0, 0.5, n1)
y = np.random.normal(0, 1, n1)
data1 = pd.DataFrame({'label': ['type1'] * n1, 'x': x, 'y': y})

# 產生type2的data
x2 = np.random.normal(2, 0.5, n2)
y2 = np.random.normal(2, 1, n2)
data2 = pd.DataFrame({'label': ['type2'] * n2, 'x': x2, 'y': y2})

# 建立 imbalanced_data
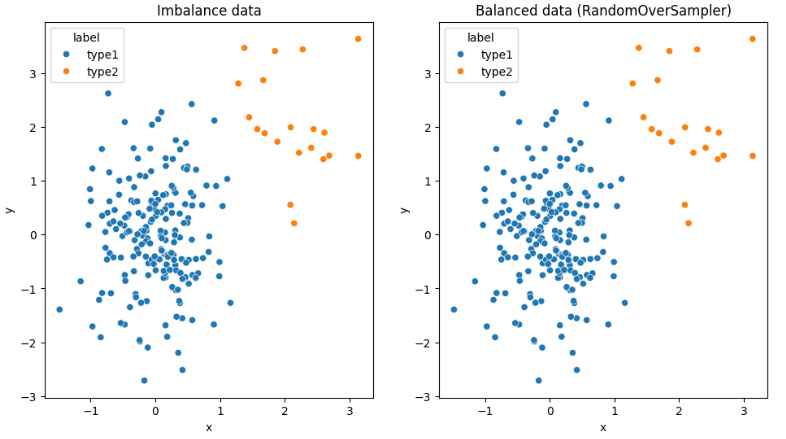
imbalance_data = pd.concat([data1, data2])
print(imbalance_data['label'].value_counts())
# type1    200
# type2     20

# 使用 RandomOverSampler 進行過採樣
oversample = RandomOverSampler(sampling_strategy='minority')
X_over, y_over = oversample.fit_resample(imbalance_data[['x', 'y']], imbalance_data['label'])
balanced_data_over = X_over
balanced_data_over['label'] = y_over
print(Counter(balanced_data_over['label']))
# Counter({'type1': 200, 'type2': 200})

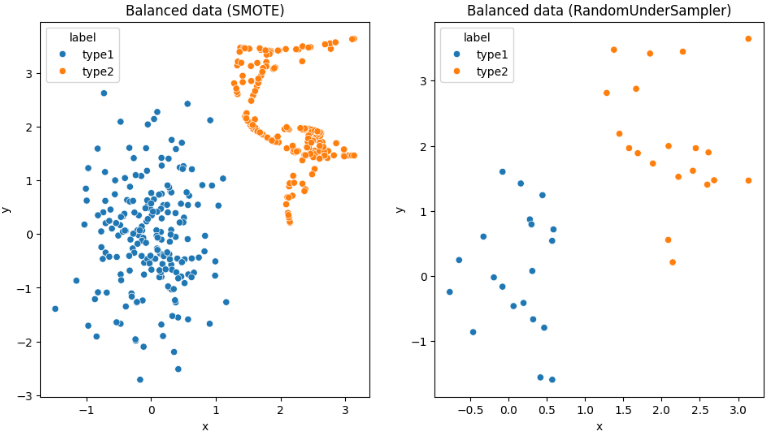
# 使用 SMOTE 進行過採樣
X_smote, label_smote = SMOTE(random_state=2022).fit_resample(imbalance_data[['x', 'y']], imbalance_data['label'])
balanced_data_smote = X_smote
balanced_data_smote['label'] = label_smote
print(Counter(balanced_data_smote['label']))
# Counter({'type1': 200, 'type2': 200})

# 使用 RandomUnderSampler 進行欠採樣
undersample = RandomUnderSampler(sampling_strategy='majority')
X_under, y_under = undersample.fit_resample(imbalance_data[['x', 'y']], imbalance_data['label'])
balanced_data_under = X_under
balanced_data_under['label'] = y_under
print(Counter(balanced_data_under['label']))
# Counter({'type1': 20, 'type2': 20})

# 繪圖
fig, axs = plt.subplots(ncols=4, figsize=(24, 6))

sns.scatterplot(data=imbalance_data, x='x', y='y', hue='label', ax=axs[0]).set(title='Imbalance data')
sns.scatterplot(data=balanced_data_over, x='x', y='y', hue='label', ax=axs[1]).set(title='Balanced data (RandomOverSampler)')
sns.scatterplot(data=balanced_data_smote, x='x', y='y', hue='label', ax=axs[2]).set(title='Balanced data (SMOTE)')
sns.scatterplot(data=balanced_data_under, x='x', y='y', hue='label', ax=axs[3]).set(title='Balanced data (RandomUnderSampler)')

plt.show()