---
tags: heartpy
---
# Heartpy套件介紹及整理
## 理論背景
> 想知道如何分析心跳，必須先了解心跳、心電圖及光體積變化描記圖法，還有什麼是心律變異度(HRV)

### 心電圖:
1. [**心電圖檢查**](https://helloyishi.com.tw/heart-health/what-is-electrocardiography/)
心電圖是一種方便、快速的心臟檢測方法，且不需額外自費。基本的心臟資訊如心跳速度、心臟電位變化等，都能由心電圖結果得知。
2. **12導程**
十二導程心電圖監視是由==十個導極==所組成的十二個導程，記錄心臟於三維空間中不同角度的電氣活動，以了解心臟各區塊之狀況。
3. **心電圖怎麼看 (PQRST波)**
- **P波**：在1次完整的心臟電位變化中，出現的第一個偏離即稱為P波。這時心房會發生去極化造成心房收縮。
- **PR段**：指的是P波到發生QRS波中間的時間段。
- **QRS波組**：QRS並非固定的排序，在命名上，波組中第一個向下偏轉的波形稱為Q波，若向上則稱為R波，而接續R波之後的負向偏轉稱為S波。值得注意的是，QRS並非3者必然同時存在，也可能出現只有QR 、QS ，或甚至只有R波的可能性。
- **ST段**：QRS波與T波中間的時間段。
- **T波**：心室再極化造成心室舒張。
- **QT間隔**：指的是心臟收縮到舒張結束的所需時間長度。有一種「長QT症候群」便是指QT間隔過長造成的心臟症狀。
:::info
:bulb:**Hint** : 若能記錄每一次左右心室的快速去極化的過程(也就是Q-R-S 段)的最高點(R點)，便能計算單位時間內的心跳數
:::

4. **心電圖三大異常波型**
- **Q波大幅下探**：代表曾有發生過心肌梗塞的狀況。
- **R波大幅上升**：可能代表有左心室肥大而引起波形放大。
- **T波倒置**：在正常的心電圖中，T波通常呈現正向偏轉，如果T發生負向偏轉，則可能代表心臟有缺血或曾發生或心肌梗塞的狀況。
### 光體積變化描記圖法(PPG):
> 當一定波長的光束照射到指端皮膚表面，每次心跳時，血管的收縮和擴張都會==影響光的透射或是光的反射==。當光照透過皮膚組織然後再反射到光敏感測器時，光照會有一定的衰減。由於動脈裡有血液的流動，那麼對光的吸收自然也有所變化。如下圖

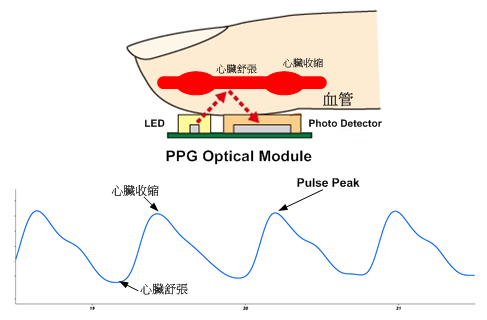
:::info
:bulb:**Hint** : 透過紀錄每次心臟收縮(數據的最高點)亦可計算單位時間內的心跳數
:::
### 心電圖(ECG) vs 光體積變化描記圖法(PPG):
> 
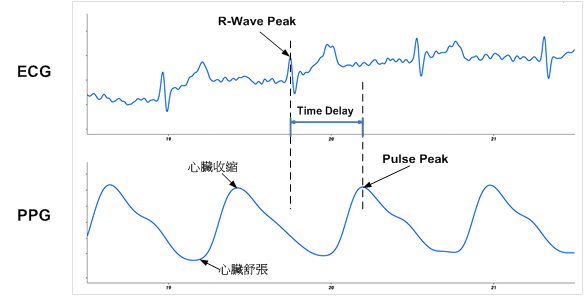
:::info
:bulb:**Hint** : 從上圖可以發現，雖然標記點並不在同一個時間點上，不過對於**計算週期性的數據並無影響**，兩者在一次心臟跳動中**恰好都有一個最高點可以紀錄**，因此本套件可以分析兩種數據。
:::
### Heart Rate Variability (HRV) 心率變異率介紹 (或稱自律神經檢測):
1. **簡述**：
一種==量測連續心跳速率變化程度==的方法，利用心跳速度的變化作為指標，間接了解自律神經的活性狀態。

2. [**臨床應用**](http://www.westgarden.com.tw/medicenter_gallery/%E5%82%BE%E8%81%BD%E9%AB%94%E5%85%A7%E6%B7%B1%E5%B1%A4%E7%9A%84%E8%81%B2%E9%9F%B3-%E8%87%AA%E5%BE%8B%E7%A5%9E%E7%B6%93%E6%AA%A2%E6%B8%AC%E5%84%80%E4%B9%8B%E8%87%A8%E5%BA%8A%E6%87%89%E7%94%A8%E8%A5%BF/)：
> 當心率變異數值愈差，未來罹患或死於心血管疾病的機率愈高。
- 當心率變異不正常，代表自律神經功能不好，也反映可能隱藏著的身心不健康。
- 預測發生心血管疾病病人的長期存活率
- 可做為個人整體健康情形的重要指標，可適用對象為不明原因失眠、心悸、胸悶、倦怠、頭暈、腸胃不適等族群

3. **測量器具**:
- 一台可以測量脈搏的儀器
- UNISAGE HRV檢測儀(台灣本土的寰碩公司所研發製造)
### [心律變異度(HRV) 名詞介紹](https://zh.m.wikipedia.org/zhtw/%E5%BF%83%E7%8E%87%E8%AE%8A%E7%95%B0%E5%88%86%E6%9E%90):
1. **Time Domain** :
> R-R代表 R心跳 和 R+1心跳 間隔的時間
- **bpm** -> the amount of heart <font color="#f00">b</font>eats <font color="#f00">p</font>er <font color="#f00">m</font>inute, 每分鐘的心跳次數
- **ibi** -> <font color="#f00">i</font>nter-<font color="#f00">b</font>eat <font color="#f00">i</font>nterval, 心跳間隔的平均距離
- **sdnn** -> 心跳間隔的標準差
- **sdsd** -> 相鄰 R-R 區間之間連續差異的標準差
- **rmssd** -> 相鄰 R-R 區間之間連續差的均方根
- **nn20** -> 心電圖中所有每對相鄰正常心跳時間間隔，差距超過20ms的數目
> nn -> normal to normal
> 也就是我們所說的RR interval（心電圖QRS的R，兩個R相間隔的時間算一次心跳時間）
- **nn50** -> 心電圖中所有每對相鄰正常心跳時間間隔，差距超過50ms的數目
- **pnn20** -> NN20數目除以量測之心電圖中所有的正常心跳間隔總數
- **pnn50** -> NN50數目除以量測之心電圖中所有的正常心跳間隔總數
- **median** absolute deviation, MAD (中位數絕對離差)
> 原數據減去中位數後，得到的新數據的絕對值的中位數
- [Poincare analysis](https://rightweightleeding.wordpress.com/2017/09/27/hrv%E9%BE%90%E5%8A%A0%E8%90%8A%E5%9C%96-poincare-plot%E5%88%86%E6%9E%90/) (SD1, SD2, S, SD1/SD2) 龐加萊分析
- [Poincare plotting](https://en.wikipedia.org/wiki/Poincar%C3%A9_plot) 龐加萊圖
2. [**Frequency Domain** :](http://www.vicon.com.tw/zh-tw/a4-646-1188/%E5%8E%9F%E7%90%86.html)
> 利用==離散傅立葉變換==將心跳間隔的時間序列轉換為頻域。一般心率變異訊號的頻譜分析使用200至500連續心跳間期穩定記錄表現，因此記錄需要數分鐘的時間。主要為==高頻區(HF 0.15-0.40赫茲)及低頻區(LF 0.04-0.15赫茲)==。高頻區通常反映副交感神經的活性，低頻區同時受到交感與副交感神經系統的調控。
- very low frequency component (0.0033–0.04 Hz), VLF
- low frequency component (0.04–0.15 Hz), LF
- high frequency component (0.15–0.4 Hz), HF
- lf/hf ratio, LF/HF
### [自律神經(HRV)檢測 vs 心電圖(EKG)](http://hrvtw.blogspot.com/2010/09/hrv_13.html):
- 自律神經(HRV)檢測的方法與做心電圖(EKG)原理步驟方法完全一致，做出來的同樣都是心電圖，只是==解讀此心電圖的角度、分析重點==不同而已。
- EKG是根據心電圖的形態(Morphplogy)、結構來判定
ex:竇房結(S-A node)、房室結(A-V node)、房室束、普金氏纖維有無阻滯異常;心肌有無病變、壞死、肥大以及心軸有無偏移
- HRV則是對同樣一份心電圖(EKG)，另外一種角度的判讀，經由觀測自律神經對竇房結(S-A node)調控的程度來判定人的自律神經生理活性(時域：SDNN)及交感副交感強度(頻域：LF、HF)
- 比較表:

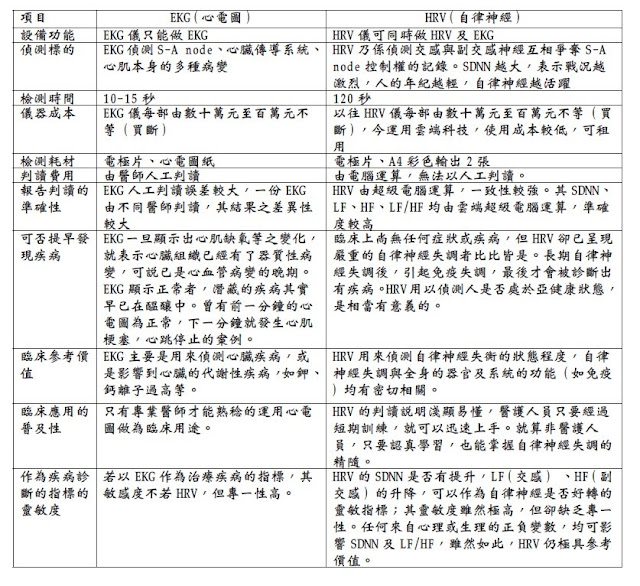
## 從開發者筆記看Heartpy
### Part1. 檢測第一個峰值併計算 BPM
> http://www.paulvangent.com/2016/03/15/analyzing-a-discrete-heart-rate-signal-using-python-part-1/
#### :star:繪製數據

import pandas as pd
import matplotlib.pyplot as plt

dataset = pd.read_csv("data.csv")

plt.title("Heart Rate Signal")
plt.plot(dataset.hart)
plt.show()


#### :star:檢測峰值
> 首先要先找到R峰的位置，需要確定Regions of Interest(ROI)
>解決方法有三種:
> - 在ROI數據點上擬合曲線，求解最大值的x位置
> - 確定ROI中每組點之間的斜率，找到斜率反轉的位置
> - 在ROI內標記數據點，找到最高點的位置
>
> 第一個提供了一個==精確的數學解決方案==，但也是計算成本最高的。後兩種方法在計算上要便宜得多，但也不太精確。在此使用第三種方法

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math

dataset = pd.read_csv("data.csv")

#Calculate moving average with 0.75s in both directions, then append to dataset
hrw = 0.75 #One-sided window size, as proportion of the sampling frequency
fs = 100 #The example dataset was recorded at 100Hz

mov_avg = dataset['hart'].rolling(int(hrw*fs)).mean() #計算移動平均
avg_hr = (np.mean(dataset.hart))
mov_avg = [avg_hr if math.isnan(x) else x for x in mov_avg]
mov_avg = [x*1.2 for x in mov_avg] 
#將平均值提高 20% 以防止繼發性心臟收縮受到干擾，在第 2 部分中，我們將動態執行此操作
dataset['hart_rollingmean'] = mov_avg

#標記ROI並找出最高點
window = [] #記錄每一輪ROI範圍
peaklist = [] #紀錄最高點位置
listpos = 0 #用一個計數器來移動不同的數據列

for datapoint in dataset.hart:
    rollingmean = dataset.hart_rollingmean[listpos]
    if (datapoint < rollingmean) and (len(window) < 1): 
	#未檢測到R-complex activity(因為len(window) < 1，所以目前沒有要檢查的ROI)
        listpos += 1
    elif (datapoint > rollingmean): #信號在平均之上，標記為ROI
        window.append(datapoint)
        listpos += 1
    else: #當信號將要掉到平均之下且等於平均的那一刻，回頭去找ROI範圍中最高的一點
        maximum = max(window)
        beatposition = listpos - len(window) + (window.index(max(window))) 
		#標記peak的位置
        peaklist.append(beatposition) 
        window = [] #重置window
        listpos += 1

ybeat = [dataset.hart[x] for x in peaklist] 
#peaklist只是最高點在x軸上的位置，還要找出最高點在y軸上的值

plt.title("Detected peaks in signal")
plt.xlim(0,2500)
plt.plot(dataset.hart, alpha=0.5, color='blue') #原資料
plt.plot(mov_avg, color ='green') #移動平均線
plt.scatter(peaklist, ybeat, color='red') #peaks
plt.show()


#### :star:計算心率
> 若要計算每分鐘心跳數(bpm)，只要計算每個R之間的距離取平均後轉換為每分鐘的值即可

RR_list = []
cnt = 0

while (cnt < (len(peaklist)-1)):
    RR_interval = (peaklist[cnt+1] - peaklist[cnt]) #計算兩點距離
    ms_dist = ((RR_interval / fs) * 1000.0) #轉換距離為時間單位
    RR_list.append(ms_dist)
    cnt += 1

bpm = 60000 / np.mean(RR_list) 
#60000 ms (1 minute) / average R-R interval of signal
print("Average Heart Beat is: %.01f" %bpm) 

> 更新繪圖及圖例

plt.title("Detected peaks in signal")
plt.xlim(0,2500)
plt.plot(dataset.hart, alpha=0.5, color='blue', label="raw signal")
plt.plot(mov_avg, color ='green', label="moving average") #移動平均線
plt.scatter(peaklist, ybeat, color='red', label="average: %.1f BPM" %bpm) 
plt.legend(loc=4, framealpha=0.6)
plt.show()


#### :star:整理成函數

> 整理程式碼為==heartbeat.py==

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math

measures = {}

def get_data(filename):
    dataset = pd.read_csv(filename)
    return dataset

def rolmean(dataset, hrw, fs):
    mov_avg = dataset['hart'].rolling(int(hrw*fs)).mean()#計算移動平均
    avg_hr = (np.mean(dataset.hart))
    mov_avg = [avg_hr if math.isnan(x) else x for x in mov_avg]
    mov_avg = [x*1.2 for x in mov_avg]
	#將平均值提高 20% 以防止繼發性心臟收縮受到干擾，在第 2 部分中，我們將動態執行此操作
    dataset['hart_rollingmean'] = mov_avg

#標記ROI並找出最高點
def detect_peaks(dataset):
    window = [] #記錄每一輪ROI範圍
    peaklist = [] #紀錄最高點位置
    listpos = 0 #用一個計數器來移動不同的數據列
    for datapoint in dataset.hart:
        rollingmean = dataset.hart_rollingmean[listpos]
        if (datapoint < rollingmean) and (len(window) < 1):
		#未檢測到R-complex activity(因為len(window) < 1，所以目前沒有要檢查的ROI)
            listpos += 1
        elif (datapoint > rollingmean):#信號在平均之上，標記為ROI
            window.append(datapoint)
            listpos += 1
        else:#當信號將要掉到平均之下且等於平均的那一刻，回頭去找ROI範圍中最高的一點
            maximum = max(window)
            beatposition = listpos - len(window) + (window.index(maximum))
			#標記peak的位置
            peaklist.append(beatposition)
            window = []#重置window
            listpos += 1
    measures['peaklist'] = peaklist
    measures['ybeat'] = [dataset.hart[x] for x in peaklist]
	#peaklist只是最高點在x軸上的位置，還要找出最高點在y軸上的值

def calc_RR(dataset, fs):
    RR_list = []
    peaklist = measures['peaklist']
    cnt = 0
    while (cnt < (len(peaklist)-1)):
        RR_interval = (peaklist[cnt+1] - peaklist[cnt])#計算兩點距離
        ms_dist = ((RR_interval / fs) * 1000.0)#轉換距離為時間單位
        RR_list.append(ms_dist)
        cnt += 1
    measures['RR_list'] = RR_list

def calc_bpm():
    RR_list = measures['RR_list']
    measures['bpm'] = 60000 / np.mean(RR_list)
	#60000 ms (1 minute) / average R-R interval of signal

def plotter(dataset, title):
    peaklist = measures['peaklist']
    ybeat = measures['ybeat']
    plt.title(title)
    plt.plot(dataset.hart, alpha=0.5, color='blue', label="raw signal")
    plt.plot(dataset.hart_rollingmean, color ='green', label="moving average")
    plt.scatter(peaklist, ybeat, color='red', label="average: %.1f BPM" %measures['bpm'])
    plt.legend(loc=4, framealpha=0.6)
    plt.show()

def process(dataset, hrw, fs): 
    rolmean(dataset, hrw, fs)
    detect_peaks(dataset)
    calc_RR(dataset, fs)
    calc_bpm()
    plotter(dataset, "My Heartbeat Plot")

import heartbeat as hb #呼叫heartbeat.py

dataset = hb.get_data("data.csv")

hb.process(dataset, 0.75, 100)

#This object contains the dictionary 'measures' with all values in it
bpm = hb.measures['bpm']

print(hb.measures.keys())

### Part2. 從心率信號中提取複雜的測量值
> http://www.paulvangent.com/2016/03/21/analyzing-a-discrete-heart-rate-signal-using-python-part-2/

> 本Part需要傅立葉轉換的概念及前面理論背景中的[HRV](https://hackmd.io/-TDtPG76T0aWMSs8z5EW2Q?view#Heart-Rate-Variability-HRV-%E5%BF%83%E7%8E%87%E8%AE%8A%E7%95%B0%E7%8E%87%E4%BB%8B%E7%B4%B9-%E6%88%96%E7%A8%B1%E8%87%AA%E5%BE%8B%E7%A5%9E%E7%B6%93%E6%AA%A2%E6%B8%AC)
#### :star:時域測量(Time Domain Measures)
> 我們還需要一些東西來計算取得我們要的資訊
> - 所有R峰的位置列表(Part1已完成)
> - 所有R-R之間的間隔列表(RR1,RR2,..,RRn)(Part1已完成)
> - R-R之間與後續R-R之間的差異列表(RRdiff1,RRdiff2,…,RRdiffn)
> - RR對之間所有後續差之間的平方差的列表
>
> 已經從Part1的detect_peaks（）函數獲得了所有R峰位置的列表，該列表包含在dict ['peaklist']中。還有來自calc_RR（）函數的RR對差異列表，位於dict ['RR_list']中

RR_diff = [] #上述之第三點的部分
RR_sqdiff = [] #上述之第四點的部分
RR_list = measures['RR_list']
cnt = 1 

while (cnt < (len(RR_list)-1)): 
    RR_diff.append(abs(RR_list[cnt] - RR_list[cnt+1])) #計算連續 R-R 區間之間的差
    RR_sqdiff.append(math.pow(RR_list[cnt] - RR_list[cnt+1], 2)) #計算平方差
    cnt += 1

print(RR_diff, RR_sqdiff)

> 有了這些東西，計算所有度量就容易多了

ibi = np.mean(RR_list) # Inter Beat Interval
print("IBI:", ibi)

sdnn = np.std(RR_list) #R-R 區間的標準差
print("SDNN:", sdnn)

sdsd = np.std(RR_diff) #所有後續 R-R 區間之間差異的標準差
print("SDSD:", sdsd)

rmssd = np.sqrt(np.mean(RR_sqdiff)) #平方差列表的均值的根
print("RMSSD:", rmssd)

nn20 = [x for x in RR_diff if (x>20)] 
nn50 = [x for x in RR_diff if (x>50)] #創建超過 20、50 的所有值的列表
pnn20 = float(len(NN20)) / float(len(RR_diff)) 
pnn50 = float(len(NN50)) / float(len(RR_diff))
#計算NN20、NN50區間佔所有區間的比例
print("pNN20, pNN50:", pnn20, pnn50)

> 當然，這些也要重新包裝到原來的heartbeat.py中

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math

measures = {}

def get_data(filename):
    dataset = pd.read_csv(filename)
    return dataset

def rolmean(dataset, hrw, fs):
    mov_avg = dataset['hart'].rolling(int(hrw*fs)).mean()#計算移動平均
    avg_hr = (np.mean(dataset.hart))
    mov_avg = [avg_hr if math.isnan(x) else x for x in mov_avg]
    mov_avg = [x*1.2 for x in mov_avg]
    #將平均值提高 20% 以防止繼發性心臟收縮受到干擾，在第 2 部分中，我們將動態執行此操作
    dataset['hart_rollingmean'] = mov_avg

#標記ROI並找出最高點
def detect_peaks(dataset):
    window = [] #記錄每一輪ROI範圍
    peaklist = [] #紀錄最高點位置
    listpos = 0 #用一個計數器來移動不同的數據列
    for datapoint in dataset.hart:
        rollingmean = dataset.hart_rollingmean[listpos]
        if (datapoint < rollingmean) and (len(window) < 1):
		#未檢測到R-complex activity(因為len(window) < 1，所以目前沒有要檢查的ROI)
            listpos += 1
        elif (datapoint > rollingmean):#信號在平均之上，標記為ROI
            window.append(datapoint)
            listpos += 1
        else:#當信號將要掉到平均之下且等於平均的那一刻，回頭去找ROI範圍中最高的一點
            maximum = max(window)
            beatposition = listpos - len(window) + (window.index(maximum))
	    #標記peak的位置
            peaklist.append(beatposition)
            window = []#重置window
            listpos += 1
    measures['peaklist'] = peaklist
    measures['ybeat'] = [dataset.hart[x] for x in peaklist]
    #peaklist只是最高點在x軸上的位置，還要找出最高點在y軸上的值

def calc_RR(dataset, fs):
    peaklist = measures['peaklist']
    RR_list = []
    cnt = 0
    
    while (cnt < (len(peaklist)-1)):
        RR_interval = (peaklist[cnt+1] - peaklist[cnt]) #計算兩點距離
        ms_dist = ((RR_interval / fs) * 1000.0) #轉換距離為時間單位
        RR_list.append(ms_dist)
        cnt += 1
    RR_diff = [] #上述之第三點的部分
    RR_sqdiff = [] #上述之第四點的部分
    cnt = 0
    
    while (cnt < (len(RR_list)-1)):
        RR_diff.append(abs(RR_list[cnt] - RR_list[cnt+1]))  #計算連續 R-R 區間之間的差
        RR_sqdiff.append(math.pow(RR_list[cnt] - RR_list[cnt+1], 2)) #計算平方差
        cnt += 1
    
    measures['RR_list'] = RR_list
    measures['RR_diff'] = RR_diff
    measures['RR_sqdiff'] = RR_sqdiff
    
def calc_ts_measures():
    RR_list = measures['RR_list']
    RR_diff = measures['RR_diff']
    RR_sqdiff = measures['RR_sqdiff']
    
    measures['bpm'] = 60000 / np.mean(RR_list)
    #60000 ms (1 minute) / average R-R interval of signal
    measures['ibi'] = np.mean(RR_list) # Inter Beat Interval
    measures['sdnn'] = np.std(RR_list) # R-R 區間的標準差
    measures['sdsd'] = np.std(RR_diff) #所有後續 R-R 區間之間差異的標準差
    measures['rmssd'] = np.sqrt(np.mean(RR_sqdiff)) #平方差列表的均值的根
    NN20 = [x for x in RR_diff if (x>20)]
    NN50 = [x for x in RR_diff if (x>50)] #創建超過 20、50 的所有值的列表
    measures['nn20'] = NN20
    measures['nn50'] = NN50
    measures['pnn20'] = float(len(NN20)) / float(len(RR_diff))
    measures['pnn50'] = float(len(NN50)) / float(len(RR_diff))
    #計算NN20、NN50區間佔所有區間的比例

def plotter(dataset, title):
    peaklist = measures['peaklist']
    ybeat = measures['ybeat']
    plt.title(title)
    plt.plot(dataset.hart, alpha=0.5, color='blue', label="raw signal")
    plt.plot(dataset.hart_rollingmean, color ='green', label="moving average")
    plt.scatter(peaklist, ybeat, color='red', label="average: %.1f BPM" %measures['bpm'])
    plt.legend(loc=4, framealpha=0.6)
    plt.show()
    
def process(dataset, hrw, fs):
    rolmean(dataset, hrw, fs)
    detect_peaks(dataset)
    calc_RR(dataset, fs)
    calc_ts_measures()
    plotter(dataset, "My Heartbeat Plot")

import heartbeat as hb #呼叫heartbeat.py

dataset = hb.get_data('data.csv')

hb.process(dataset, 0.75, 100)

hb.measures['bpm']
hb.measures['ibi']
hb.measures['sdnn']

print("bpm: %f" %hb.measures['bpm'])
print("ibi: %f" %hb.measures['ibi'])
print("sdnn: %f" %hb.measures['sdnn'])
print("sdsd: %f" %hb.measures['sdsd'])
print("rmssd: %f" %hb.measures['rmssd'])
print("pnn20: %f" %hb.measures['pnn20'])
print("pnn50: %f" %hb.measures['pnn50'])

#### :star:頻域測量(Frequency Domain Measures)
> - 頻域測量並不是要將心率傳換為頻域，這樣只會回傳 bpm / 60 的強頻域
> - 我們將==RR間隔==轉換到頻域，隨著身體需求的變化，心率隨著時間的變化而變化。這種變化表現為心跳之間的距離隨時間變化（之前計算的RR間隔）
> - 首先畫出RR間隔

RR_list = measures['RR_list']
plt.title(title)
plt.xlim(0,25)
plt.ylim(900, 1200)
plt.plot(RR_list, alpha=0.5, color='blue')
plt.show()

> 圖中可以看到，RR間隔不會隨心跳而劇烈變化，而是隨時間呈正弦波狀變化（不同正弦波的組合）。但是，任何傅立葉變換方法都依賴於均勻間隔的數據，並且RR間隔在時間上肯定不是均勻間隔的。這是因為間隔的時間位置取決於長度，每個間隔都不同。
> 我們還需要:
> - 創建一個帶有RR間隔的均勻間隔的時間線
> - 內插信號，既可以創建均勻間隔的時間序列，又可以提高分辨率
> - 在某些研究中，此插值步驟也稱為重新採樣
> - 將信號轉換到頻域
> - 積分頻譜的LF和HF部分下方的面積
>
> 首先，我們先創建一個帶有RR間隔的均勻間隔的時間線

from scipy.interpolate import interp1d 

peaklist = measures['peaklist'] 

RR_list = measures['RR_list']
RR_x = peaklist[1:] #刪除第一個位置，因為第一個間隔分配給第二個節拍
RR_y = RR_list #Y 值等於區間長度
RR_x_new = np.linspace(RR_x[0],RR_x[-1],RR_x[-1]) 
#從第二個峰值開始創建均勻間隔的時間線，其端點和長度等於最後一個峰值的位置
f = interp1d(RR_x, RR_y, kind='cubic') 
#使用 cubic spline interpolation進行插值
plt.title("Original and Interpolated Signal")
plt.plot(RR_x, RR_y, label="Original", color='blue')
plt.plot(RR_x_new, f(RR_x_new), label="Interpolated", color='red')
plt.legend()
plt.show()

> 現在使用numpy的快速傅立葉變換 np.fft.fft() 方法，計算樣本間距，將樣本轉換為 Hz 並繪製

#設置變量
n = len(dataset.hart) 
frq = np.fft.fftfreq(len(dataset.hart), d=((1/fs))) #將 bin 劃分為頻率類別
frq = frq[range(int(n/2))] #獲取頻率範圍的一側

#FFT
Y = np.fft.fft(f(RR_x_new))/n #計算 FFT
Y = Y[range(int(n/2))] #回傳 FFT 的一側

#Plot
plt.title("Frequency Spectrum of Heart Rate Variability")
plt.xlim(0,0.6) 
#將 X 軸限制為感興趣的頻率（0-0.6Hz 可見性，我們對 0.04-0.5 感興趣）
plt.ylim(0, 50)
plt.plot(frq, abs(Y))
plt.xlabel("Frequencies in Hz")
plt.show()

> 可以清楚地看到信號中的LF和HF頻率峰值。最後一件事就是對LF（0.04 – 0.15Hz）和HF（0.16 – 0.5Hz）頻帶下的曲線下面積進行積分。我們需要找到與感興趣的頻率範圍相對應的數據點。在FFT期間，計算了單側頻率範圍frq，因此可以在其中搜索所需的數據點位置

lf = np.trapz(abs(Y[(frq>=0.04) & (frq<=0.15)])) 
#Sx 介於 0.04 和 0.15Hz (LF) 之間的 lice 頻譜，並使用 NumPy 的trapz函數找到該區域
print("LF:", lf)

hf = np.trapz(abs(Y[(frq>=0.16) & (frq<=0.5)])) #0.16-0.5Hz (HF)
print("HF:", hf)

> HF 與呼吸有關，LF 與短期血壓調節有關。
### Part3. 信號過濾、通過動態閾值改進檢測
> http://www.paulvangent.com/2016/03/30/analyzing-a-discrete-heart-rate-signal-using-python-part-3/

> 目前我們已經可以分析理想數據的時域及頻域部分，現在要來試試有受到外界因素干擾的數據(噪音、偽影、傳感器移動、參與者可能會打噴嚏、移動)
> 我們將這樣處理問題:
> - 將該信號傳遞給算法的結果
> - 注意採樣頻率
> - 過濾信號以去除不想要的頻率（噪音）
> - 動態閾值提高檢測精度
> - 檢測錯誤/錯過的峰
> - 消除錯誤並將RR信號重構為無錯誤
#### :star:導入新數據
> 這是data2.csv的數據呈現圖形

> 現在導入原本寫好的程式碼中

> detect_peaks（）函數將在一種情況下中斷：當心率信號從小於移動平均線變為等於而連續至少兩個數據點都沒有移動到其上方時，發生這種情況的最可能情況是信號在一段時間內下降到零。然後，該函數將跳到else，並嘗試檢測ROI中的峰值，但是由於信號從未上升到移動平均線之上，因此未標記ROI，因此max（window）回傳錯誤，因為空列表沒有最大值。

> 現在要更新detect_peaks（）函數：

def detect_peaks(dataset):
    window = []
    peaklist = []
    listpos = 0
    
    for datapoint in dataset.hart:
        rollingmean = dataset.hart_rollingmean[listpos]
        if (datapoint <= rollingmean) and (len(window) <= 1): 
	#這是要更新的地方(datapoint <= rollingmean)、(len(window) <= 1)
            listpos += 1
        elif (datapoint > rollingmean):
            window.append(datapoint)
            listpos += 1
        else:
            maximum = max(window)
            beatposition = listpos - len(window) + (window.index(max(window)))
            peaklist.append(beatposition)
            window = []
            listpos += 1
    
    measures['peaklist'] = peaklist
    measures['ybeat'] = [dataset.hart[x] for x in peaklist]

> 還有一個地方要註解掉

def rolmean(dataset, hrw, fs):
    mov_avg = dataset['hart'].rolling(int(hrw*fs)).mean()#計算移動平均
    avg_hr = (np.mean(dataset.hart))
    mov_avg = [avg_hr if math.isnan(x) else x for x in mov_avg]
    #mov_avg = [x*1.2 for x in mov_avg]
    #這裡要將此行註解掉
    dataset['hart_rollingmean'] = mov_avg

> 模型不再回傳錯誤並且正在檢測峰值，但這不是我們正在尋找的結果。讓我們從降噪開始，看看是否可以改善信號

#### :star:採樣頻率
> 在信號過濾之前要先確定信號的採樣率，之前的兩個Part都是100Hz。實際的記錄頻率可能隨不同的設備或系統而變化，也可能與設備的額定值略有不同。所有計算得出的度量的準確性取決於準確了解採樣率，因此進行檢查非常重要。通常在每條數據線上記錄“世界時間”或“自開始記錄以來的時間”，以便之後計算和驗證採樣率。

sampletimer = [x for x in dataset.timer] 
#dataset.timer 是一個毫秒計數器，記錄開始於“0”
measures['fs'] = ((len(sampletimer) / sampletimer[-1])*1000) 
#將數據集的總長度除以最後一個計時器條目。這是在毫秒，所以乘以 1000 得到赫茲值
#如果您的計時器是日期時間字串，請轉換為 UNIX 時間以便輕鬆計算，請使用以下內容：
unix_time = []

for x in dataset.datetime:
    dt = datetime.datetime.strptime(Datum, "%Y-%m-%d %H:%M:%S.%f")
    unix_time.append(time.mktime(dt.timetuple()) + (dt.microsecond / 1000000.0))

measures['fs'] = (len(unix_time) / (unix_time[-1] - unix_time[0]))

> 這裡提供的文件的採樣率實際上是 117Hz！現在可以使用確定的採樣率自動計算測量值
>
> 除了採樣率之外，您還應該檢查數據的採樣分佈，所有樣本均間隔均勻，例如數據流中是否沒有“間隙”或“跳過”？如果您的數據包含間隙和跳躍，只要它們最多只有幾個樣本長，請考慮在處理之前對缺失值進行插值
>
> 現在我們知道了採樣頻率，我們可以進行信號濾波
#### :star:信號過濾
> [巴特沃斯濾波器(Butterworth）](https://zh.wikipedia.org/wiki/%E5%B7%B4%E7%89%B9%E6%B2%83%E6%96%AF%E6%BB%A4%E6%B3%A2%E5%99%A8)

from scipy.signal import butter, lfilter 

#filter
def butter_lowpass(cutoff, fs, order=5):
    nyq = 0.5 * fs #Nyquist 頻率是採樣頻率的一半
    normal_cutoff = cutoff / nyq
    b, a = butter(order, normal_cutoff, btype='low', analog=False)
    return b, a

def butter_lowpass_filter(data, cutoff, fs, order):
    b, a = butter_lowpass(cutoff, fs, order=order)
    y = lfilter(b, a, data)
    return y

dataset = get_data('data2.csv')
dataset = dataset[6000:12000].reset_index(drop=True) 
#為了可見性，從樣本 6000 - 12000 (00:01:00 - 00:02:00) 中選擇整個信號
filtered = butter_lowpass_filter(dataset.hart, 2.5, 100.0, 5)
#用 2.5Hz 的截止頻率和 5 階巴特沃斯濾波器過濾信號

#Plot it
plt.subplot(211)
plt.plot(dataset.hart, color='Blue', alpha=0.5, label='Original Signal')
plt.legend(loc=4)
plt.subplot(212)
plt.plot(filtered, color='Red', label='Filtered Signal')
plt.ylim(200,800)
plt.legend(loc=4)
plt.show()


> 若仔細觀察，可以發現信號稍微平滑一點
#### :star:使用動態閾值提高檢測精度
> 減少次峰錯誤標記的第一個也是最明顯的方法是提高我們用作閾值的移動平均值，但是提升到什麼水平呢？
> - 查看信號長度並計算有多少峰值與我們預期的峰值
> - 確定並使用 RR 區間的標準差（RRSD）
>
> 檢測到的峰值數量只能用於拒絕明顯不正確的閾值，例如:坐著不動時，拒絕導致平均 bpm <30bpm 和 >130bpm 的閾值，其他情況下（體育鍛煉）閾值亦可能不同
>
> RRSD 告訴我們所有 RR 間隔之間的差異是如何分散的。一般來說，如果沒有太多的噪音，同時具有不為零的最低 RRSD 和可信的 BPM 值的檢測將是最佳的
>
> ==RRSD 不能為零==，因為這意味著沒有心率變異性，這強烈==表明檢測 R 峰時出現錯誤==
>
> 錯過一個節拍會導致 RR 間隔大約是平均 RR 間隔的兩倍，而錯誤地標記一個節拍會導致一個 RR 間隔最多大約是平均 RR 間隔的一半, 但一般較小
>
> 評估最可能的 RRSD 和 BPM 對

def detect_peaks(dataset, ma_perc, fs): #更改函數以接受移動平均百分比“ma_perc”參數
    rolmean = [(x+((x/100)*ma_perc)) for x in dataset.hart_rollingmean] 
    #使用傳遞的 ma_perc 提高移動平均線
    window = [] #記錄每一輪ROI範圍
    peaklist = [] #紀錄最高點位置
    listpos = 0 #用一個計數器來移動不同的數據列
    
    for datapoint in dataset.hart:
        rollingmean = rolmean[listpos]
        if (datapoint <= rollingmean) and (len(window) <= 1):
	#未檢測到R-complex activity(因為len(window) < 1，所以目前沒有要檢查的ROI)
            listpos += 1
        elif (datapoint > rollingmean):#信號在平均之上，標記為ROI
            window.append(datapoint)
            listpos += 1
        else:#當信號將要掉到平均之下且等於平均的那一刻，回頭去找ROI範圍中最高的一點
            maximum = max(window)
            beatposition = listpos - len(window) + (window.index(max(window)))
			#標記peak的位置
            peaklist.append(beatposition)
            window = [] #重置window
            listpos += 1
    
    measures['peaklist'] = peaklist
    measures['ybeat'] = [dataset.hart[x] for x in peaklist]
    #peaklist只是最高點在x軸上的位置，還要找出最高點在y軸上的值
    measures['rolmean'] = rolmean
    calc_RR(dataset, fs)
    measures['rrsd'] = np.std(measures['RR_list'])

def fit_peaks(dataset, fs):
    ma_perc_list = [5, 10, 15, 20, 25, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 150, 200, 300] 
    #列出移動平均增加百分比，盡可能詳細，但要注意速度
    rrsd = []
    valid_ma = []
    
    for x in ma_perc_list: #檢測所有百分比的峰值，將結果附加到列表“rrsd”
        detect_peaks(dataset, x, fs)
        bpm = ((len(measures['peaklist'])/(len(dataset.hart)/fs))*60)
        rrsd.append([measures['rrsd'], bpm, x])
    
    for x,y,z in rrsd: #測試列表條目並選擇有效措施
        if ((x > 1) and ((y > 30) and (y < 130))):
            valid_ma.append([x, z])
   
    measures['best'] = min(valid_ma, key = lambda t: t[0])[1] 
    #保存 ma_perc 以供以後繪製
    detect_peaks(dataset, min(valid_ma, key = lambda t: t[0])[1], fs) 
    #檢測具有最低 rrsd 的“ma_perc”峰值

#### :star:找檢測錯誤的峰
> 最後要看的是如何檢測和淘汰異常峰位，其中一種方法是利用心率逐漸變化而不是突然變化。例如，您的 bpm 不會在一個節拍中從 60bpm 跳到 120bpm，反之亦然。這再次意味著返回到 RR 間隔，如果在檢測中跳過了一個峰值，或者標記了兩個峰值而不是一個，則生成的 RR 間隔將比平均間隔大很多或小很多。我們可以設置一個閾值並標記超過它的間隔，類似於我們檢測峰值的方式。然而，還有一個潛在的問題，如果一次分析一個很長的信號，其中心率隨時間變化很大，這可能會導致錯誤的淘汰，如果一個心率逐漸增加的信號，從 60 bpm 開始，到 180 bpm 結束。這意味著減少 RR 間隔的穩定趨勢，這表明心率加快，而非 R 峰檢測錯誤，如果這發生在數據中，可以先去除 RR_list 的趨勢

from scipy import signal

RR_list = measures['RR_list'] 
RR_list_detrended = signal.detrend(RR_list, type='linear')

> 但是，如果信號包含一段時間的大幅增加，然後是類似的大幅下降的心率，可能需要使用截止頻率非常低的高通濾波器。另一種方法可能是將信號分成更小的部分（以便分離增加和減少趨勢），線性去趨勢並平均測量值。如果較小的部分長度不相等，請務必在平均之前對這些度量進行加權
>
> 當然，不要用去趨勢的 RR 信號計算任何度量，僅將其用於檢測峰值標記中的錯誤。
>
> 回到異常值淘汰。對於閾值，在實踐中發現 RR 差異平均值的閾值水平，兩端都有 250-300 毫秒的頻帶效果很好。使用前面的代碼並將數據集限制為 [5000:15000]（暫時排除嘈雜的開頭），像這樣實現

RR_list = measures['RR_list']
peaklist = measures['peaklist']
ybeat = measures['ybeat']
upper_threshold = (np.mean(RR_list) + 300) #設置閾值
lower_threshold = (np.mean(RR_list) - 300)
#檢測異常值
cnt = 0
removed_beats = []
removed_beats_y = []
RR2 = []
while cnt < len(RR_list):
    if (RR_list[cnt] < upper_threshold) and (RR_list[cnt] > lower_threshold):
        RR2.append(RR_list[cnt])
        cnt += 1
    else:
        removed_beats.append(peaklist[cnt])
        removed_beats_y.append(ybeat[cnt])
        cnt += 1
measures['RR_list_cor'] = RR2 #將更正的 RR 列表附加到字典
plt.subplot(211)
plt.title('Marked Uncertain Peaks')
plt.plot(dataset.hart, color='blue', alpha=0.6, label='heart rate signal')
plt.plot(measures['rolmean'], color='green')
plt.scatter(measures['peaklist'], measures['ybeat'], color='green')
plt.scatter(removed_beats, removed_beats_y, color='red', label='Detection uncertain')
plt.legend(framealpha=0.6, loc=4)
plt.subplot(212)
plt.title("RR-intervals with thresholds")
plt.plot(RR_list)
plt.axhline(y=upper_threshold, color='red')
plt.axhline(y=lower_threshold, color='red')
plt.show()

> 結果是所有正確檢測到的 R 峰標記為綠色的點，不正確的標記為紅色。生成的列表measures['RR_list_cor'] 具有RR 列表，其中不包含屬於不正確峰的那些。
:::danger
:negative_squared_cross_mark: 目前實作在採樣頻率中遇到BUG且後面的程式碼塞不進原有程式碼
:::
### Part4. 檢測和拒絕噪聲信號部分(正在開發中)
## 實際套用Heartpy分析
> 首先，我們將使用與 HeartPy 打包的示例數據集來做測試。

import heartpy as hp
import matplotlib.pyplot as plt

> HeartPy 帶有一個函數 load_exampledata() 可以加載提供的數據集。它將返回一個元組（數據，計時器），其中“計時器”是計時器列（毫秒或日期時間）。如果沒有可用的計時器列，則仍返回一個元組，但計時器數組為空。
> HeartPy 包含三個數據集:
> - 0：一個短的、非常乾淨的 PPG 信號，以 100.0 Hz 採樣
> - 1：稍長（約 2 分鐘）的 PPG 信號，前三分之一缺失信號，其餘信號出現隨機噪聲尖峰
> - 2：在駕駛模擬器中使用食指上的脈衝傳感器和 Arduino 駕駛時記錄“在野外”記錄的長（約 11.5 分鐘）PPG 信號
>
> 我們將測試所有三個例子並對每個示例進行分析。
### 第一個數據分析:

data, timer = hp.load_exampledata(0)

plt.figure(figsize=(12,4))
plt.plot(data)
plt.show()

**這是一個完美的信號，分析應該沒有問題**
> 運行 hp.process() 時，會返回兩個 dicts：working_data（包含您可能仍希望訪問的工作數據，例如峰值位置和峰值-峰值間隔）和measures（包含計算的輸出度量）。
> 在文檔中，我們將它們縮寫為 'wd' 和 'm'

wd, m = hp.process(data, sample_rate = 100.0)

**可視化分析結果**
> Heartpy 帶有一個函數 **hp.plotter(wd, m)** 來做這件事。該函數要求您為其提供working_data 和measures dict。
>
> 如果在調用 **hp.plotter(wd, m)** 之前向 matplotlib 指定圖形大小等參數，將使用指定的圖形大小。

plt.figure(figsize=(12,4))

hp.plotter(wd, m)

for measure in m.keys():
    print('%s: %f' %(measure, m[measure]))

### 第二個數據分析:

data, timer = hp.load_exampledata(1)

plt.figure(figsize=(12,4))
plt.plot(data)
plt.show()

> 這是一個更棘手的信號。在開始錄製之前和戴上傳感器時，一開始沒有信號。信號開始後，當我在錄製時用力移動傳感器時，會出現一些噪音尖峰。這也模仿了在“野外”錄製時可能發生的情況，如參與者移動並意外拉扯傳感器電纜。

sample_rate = hp.get_samplerate_mstimer(timer)

wd, m = hp.process(data, sample_rate)

plt.figure(figsize=(12,4))
hp.plotter(wd, m)

for measure in m.keys():
    print('%s: %f' %(measure, m[measure]))

:::info
:bulb:請注意，我們從計時器列（以 ms 值表示）計算了 sample_rate。這一點很重要，因為我們不知道信號的採樣率是多少。所有措施都取決於了解採樣率。
:::
> HeartPy 帶有兩個函數：hp.get_samplerate_mstimer()，它基於 ms-timer 計算採樣率，以及 hp.get_samplerate_datetime()，它基於 datetime 值中的列計算 sample_rate
### 第三個數據分析:
> 之前看到了如何使用 mstimer，現在讓我們看一下使用日期時間字符串對時間進行編碼的“野外”記錄：

data, timer = hp.load_exampledata(2)

print(timer[0])

> 在計算採樣率時，我們需要給 get_samplerate_datetime() 字符串的格式（默認情況下它需要 HH:MM:SS.ms）：

sample_rate = hp.get_samplerate_datetime(timer, timeformat='%Y-%m-%d %H:%M:%S.%f')

print('sample rate is: %f Hz' %sample_rate)

> sample rate is: 100.419711 Hz

wd, m = hp.process(data, sample_rate, report_time = True)

plt.figure(figsize=(12,4))
hp.plotter(wd, m)

#放大一點
plt.figure(figsize=(12,4))
plt.xlim(20000, 30000)
hp.plotter(wd, m)

for measure in m.keys():
    print('%s: %f' %(measure, m[measure]))