# Movimiento armónico simple Consideramos un bloque de masa $m$ unido al extremo de un resorte  --- * posición de equilibrio $x=0$ * El sistema oscila si se perturba  --- ## Ley de Hooke $$ F_{resorte}=-Kx $$ * Fuerza restauradora o de restitución * K es la constante de restitución  --- ¿Qué pasa si el bloque se desplaza hacia la derecha de x=0?, ¿y a la izquierda?  --- <!-- .slide: data-background="#1A237E" --> Pregunta 1: Un bloque en el extremo de un resorte se jala a la posición $x=A$ y se libera desde el reposo. En un ciclo completo de su movimiento ¿qué distancia recorre? --- # Partícula en movimiento armónico simple --- Partimos de la segunda ley de Newton $$F=ma$$ Aquí, la fuerza es la fuerza del resorte ejercida sobre la masa. 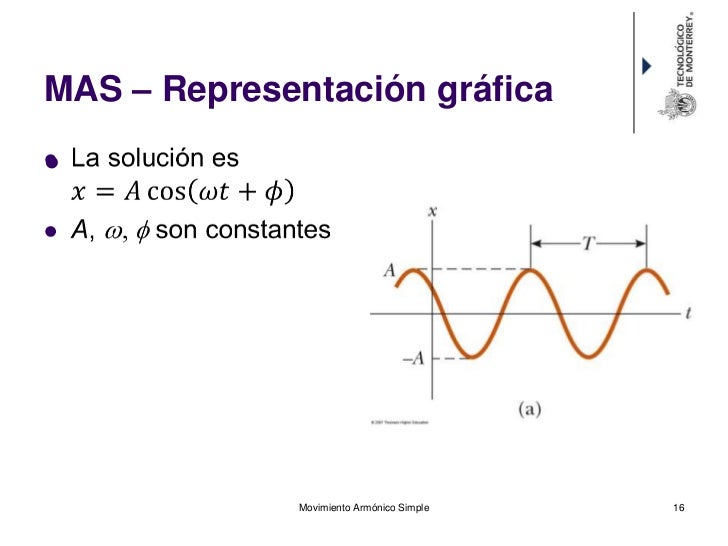Así $$-Kx=ma$$ Hacemos $\omega=\sqrt{\frac{K}{m}}$ --- y se pude reescribir como $$\frac{d^2x}{dt^2}=-\omega^2x$$ cuya solución puede escribirse como $$ x(t)=A\cos(\omega t + \phi) $$ donde $A$, $\omega$ y $\phi$ son constantes. --- Para mostrar que esta solución satisface la ecuación, notemos que $$\frac{dx}{dt}=A\frac{d}{dt}\cos(\omega t +\phi) = -\omega A \sin(\omega t +\phi)$$ y $$\frac{d^2x}{dt^2}=-\omega A \frac{d}{dt} \sin(\omega t +\phi)=-\omega^2A\cos(\omega t +\phi)$$ --- por lo que $$\frac{d^2x}{dt^2}=-\omega^2x$$ ---  --- * $A$ es la amplitud de la oscilación (m,cm,...) * $T$ es el periodo (s) * $\omega$ es la frecuencia angular (rad/s) * $\phi$ es la constante de fase (o fase inicial) La función $x(t)$ es periodica y su valor y su valor es el mismo cada vez que $\omega t$ aumenta en $2\pi$ radianes --- Pregunta: ¿Cuál es el perido de la función $x=A\cos(\omega t + \phi)$? --- Respuesta: Periodo = $\frac{2\pi}{\omega}$ --- En general * Periodo es $T=\frac{2\pi}{\omega}$ medido en Segundos * Frecuencia $f=\frac{1}{T}$ en $s^{-1}$ o Hertz * Frecuencia angular $\omega=2\pi f$ en $rad/s$ --- <!-- .slide: data-background="#1A237E" --> Pregunta: Un objeto de masa $m$ cuelga de un resorte y se pone en oscilación. El periodo de la oscilación se mide y se registra como $T$. El objeto de masa $m$ se retira y se sustituye con un objeto de masa $2m$. Cuando este objeto se pone en oscilación, ¿cuál es el periodo del movimiento? 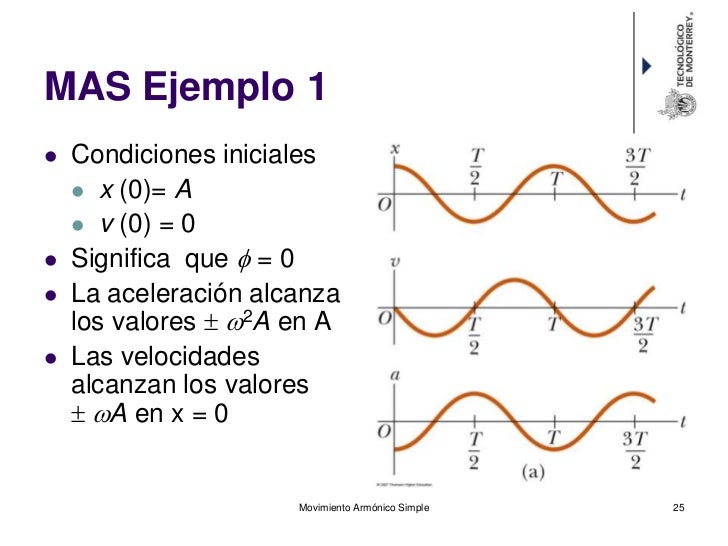* $2T$ * $\sqrt 2T$ * $T$ * $T/\sqrt 2$ * $T/2$ --- **Velocidad y Aceleración** Es posible obtener la velocidad y aceleración a partir de tomar las derivadas. Si $x(t)=A \cos(\omega t +\phi)$ $$v=\frac{dx}{dt}=-\omega A \sin(\omega t + \phi)$$ y $$a=\frac{d^2x}{dt^2}=-\omega^2A\cos(\omega t +\phi)$$ --- Los valores máximos de velocidad y aceleración son $$v_{max}=\omega A$$ $$a_{max}=\omega^2 A$$ ---  ---