Instructions for Hopin:
* Doble click on the shared screen to maximize it, also you can press F11 to get a full-screen of the navigator.
* If you want to reduce the size of the comment section click on the button “|>” on the right-upper aside a green point.

---

## ML vs QM


---
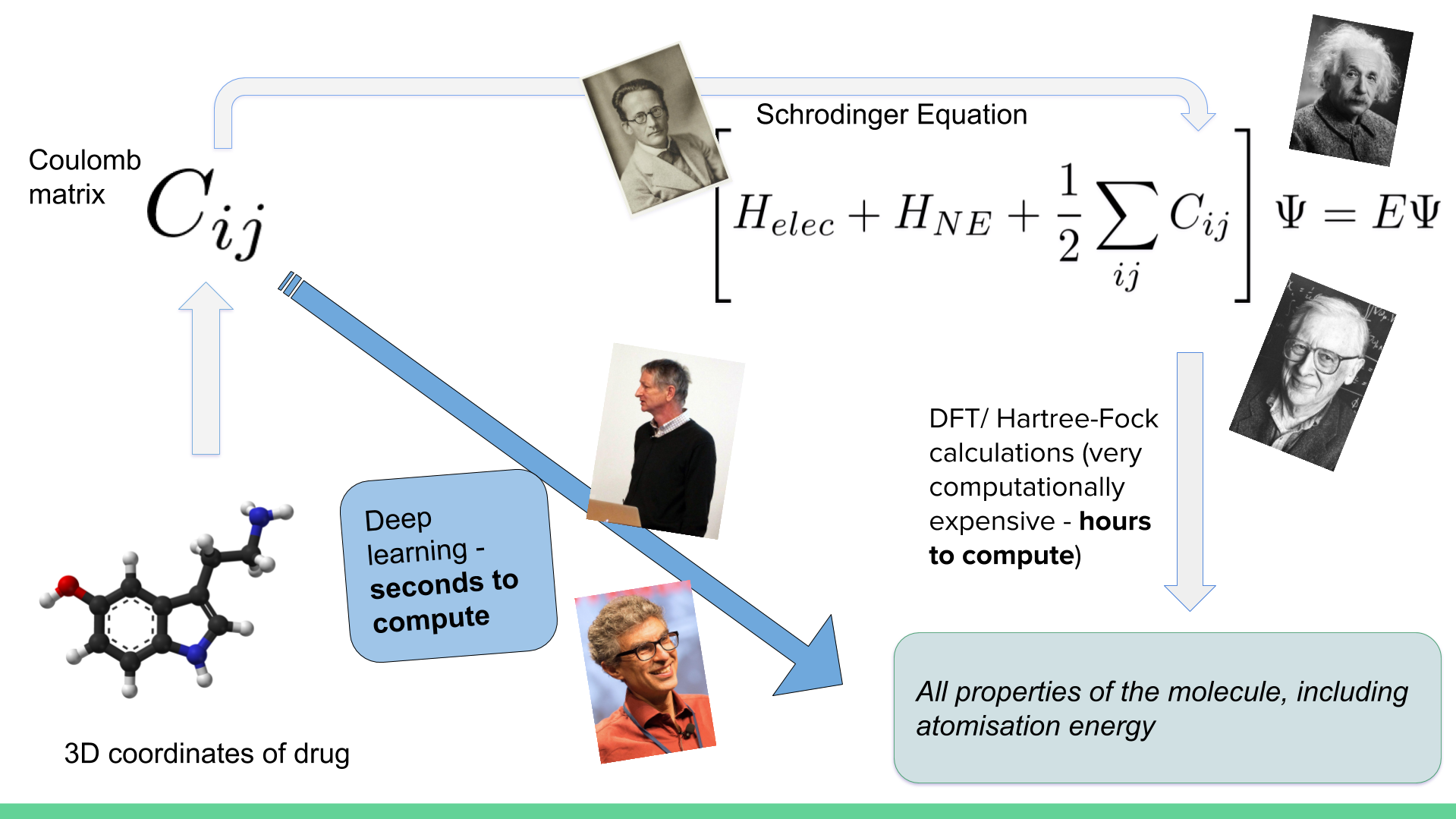
# Linea de tiempo
* 2007
* 2012
* 2015
* 2018

---

# (2007) Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces
Jorg Behler and Michele Parrinello
PRL 98, 146401 (2007)

---

---

The general structure of this network topology is shown schematically for a system consisting of three atoms.

---

The main idea is to represent the total energy $E$ of the system as a sum of atomic contributions $E_i$, (typically used in empirical potentials)

$$E=\sum_i E_i$$

---
**Radial symmetry functions** are constructed as a sum of Gaussians with the parameters $\eta$ and $R_s$
$$G_i^1=\sum_{j\ne i}^{all} e^{-\eta (R_{ij}-R_s)^2}f_c(R_{ij})$$

*The summation over all neighbors $j$ ensures the independence of the coordination number*.

---

**Angular terms** are constructed for all triplets of atoms by summing the cosine values of the angles $\theta_{ijk}=\frac{\vec{R}_{ij}\vec{R}_{ij}}{R_{ij}R_{ij}}$ centered at atom $i$,
$$ G_i^2=2^{1-\zeta}\sum_{j,k\ne i}^{all}(1+\lambda \cos \theta _{ijk})^{\zeta}\times e^{-\eta(R^2_{ij}+R^2_{ik}+R^2_{jk})}f_c(R_{ij})f_c(R_{ik})f_c(R_{jk})$$

---

*We note that the $G_i^{\mu}$ depend on all atomic positions inside the cutoff radius and thus represent "many body" terms.*

<figure>
<center>
<img src='https://pubs.rsc.org/image/article/2017/SC/c7sc02267k/c7sc02267k-f1_hi-res.gif' width="400"/>
<figcaption>DOI: 10.1039/C7SC02267K (Edge Article) Chem. Sci., 2017, 8, 6924-6935</figcaption></center>
</figure>
---

# Descriptores

---

# (2012) Coulomb Matrix
**Phys. Rev. Lett. 108, 058301 – Published 31 January 2012**
<figure>
<center>
<img src='https://pubs.rsc.org/image/article/2018/sc/c7sc02664a/c7sc02664a-t3_hi-res.gif' width="400"/>
</center>
</figure>

<figure>
<center>
<img src='https://github.com/napoles-uach/figuras/blob/master/coulMat.png?raw=true' width="400"/>
</center>
</figure>

<figure>
<center>
<img src='https://storage.googleapis.com/groundai-web-prod/media%2Fusers%2Fuser_228265%2Fproject_354684%2Fimages%2Fx1.png' width="400"/>
</center>
</figure>

---
# (2015) Bag of Bonds
**J. Phys. Chem. Lett. 2015, 6, 12, 2326–2331**
In the BoB model, first the molecular Hamiltonian is mapped to a well-defined **descriptor**, here a vector composed of bags, where each bag represents a particular bond type (C-C, C-N, and so on). Motivated by the Coulomb matrix concept, each entry in every bag is computed as $Z_iZ_j/|\vec{R}_i-\vec{R}_j|$.


The energy of a molecule with a BoB vector $\mathbf{M}$ is written as a sum over weighted exponentials centered on every molecule $I$ in the training set
$$E_{BoB}(\mathbf{M})=\sum_{I=1}^N \alpha_I \exp(-d(\mathbf{M},\mathbf{M_I})/\sigma)$$
where $d(\mathbf{M},\mathbf{M_I})=\sum_j||M^j-M^J_I||_p$ and $I$ runs over all molecules $M_I$ in the training set of size $N$.

---
# Understanding molecular representations in machine learning
**B. Huang & A. von Lilienfeld, J. Chem. Phys. 145, 161102 (2016)**

---

# Message Passing

# (2017) Neural Message Passing for Quantum Chemistry
Gilmer et. al, arXiv (2017)


During the message passing phase, hidden states $h_v^t$ at each node in the graph are updated based on messages $m_v^{t+1}$ according to

$$ m_v^{t+1}= \sum_{w \in N(v)} M_t(h_v^t,h_w^t,e_{vw})$$

where in the sum, $N(v)$ denotes the neighbors of $v$
in the graph $G$.

The readout phase computes a feature vector for the whole graph using some readout function $R$ according to

$$ \hat{y} = R\left( \{ h_v^T | v \in G \} \right) $$

The message functions $M_t$, vertex update $U_t$, and $R$ are all learned differentiable functions.

---

# The Graph Convolutional Network is the simplest version of namely the message passing neural network:

$$ H^{(l+1)} = \sigma (AH^{(l)}W^{(l)}) $$

---

# (2018) Deeply learning molecular structure-property relationships using attention- and gate-augmented graph convolutional network,

Seongok Ryu and Jaechang Lim and S. H. Hong and W. Y. Kim,
arXiv,2018

# GCN, GCN+attention

For molecular applications, the attention coefficient should be analogous to the interaction strength between an atom par (i,j)


---