---
lang: ja-jp
tags: Survey, merpay
---
# MPML
:::danger
~~**武闘派**の方に向けた資料です．**理論派**に向けた資料ではありません．~~
:::

> 群論は足し算の抽象化
> もうちょっと言うと，集合と，集合のタプルの間の操作の集合
> 正方行列の積とか．

## @moriakiの野望
[ratm](https://github.com/moriaki3193/ratm)パッケージを作成して，[コンペ](https://atma.connpass.com/event/138332/)で善戦したい．

## Planning
1. **20190724**: [Parallel GBDT](http://zhanpengfang.github.io/418home.html)（and [Factorization Machines](https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf)）
2. **next**: [Gradient Boosting Factorization Machines](http://tongzhang-ml.org/papers/recsys14-fm.pdf) or [DeepFM](https://arxiv.org/abs/1803.05170)
3. **next**: [DeepGBM](https://github.com/motefly/DeepGBM)

GBRT ────┐
         ├─ GBFM ───┐
FM ──────┤          ├─ DeepGBM
         ├─ DeepFM ─┘
DNN ─────┘

- Gradient Boosting系の手法は汎用的で高精度
- Factorization Machines系の手法はスパースな特徴量について交互作用の影響の推定が得意
- DNN系の手法は高次の交互作用を考慮するのが得意？

## Parallel Gradient Boosting Regression Tree
### Goals
- 勾配Boostingの手法としてGBDTがおさらいできる
- 高速化のためのアルゴリズムと実装がわかる
- 一般に公開されている実装の一覧を把握できる

### Useful links
- [Parallel Gradient Boosting Decision Trees](http://zhanpengfang.github.io/418home.html) by @zhanpenf
- [SparkTree: Push the Limit of Tree Ensemble Learning](https://www.microsoft.com/en-us/research/wp-content/uploads/2017/04/main.pdf) by Microsoft Research (MSR)
- [From RankNet to LambdaRank to LambdaMART: An Overview](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.180.634&rep=rep1&type=pdf) by C.Burges (MSR)
- 去年のインターンで実装した[LambdaMART on PySpark](https://github.com/kouzoh/mercari-ltr/tree/feature/lambdamart/models/LambdaMART) by @moriaki

### Background
- GBRT系の手法はKaggleなどのコンペでよく利用される汎用的なアルゴリズム
- 基本的には回帰の手法だが，Pairwise損失に落とし込むことで分類問題にも応用可能
- 情報検索の領域だとこの手法を応用した[LambdaMART](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.180.634&rep=rep1&type=pdf)がよくSOTA手法のベースラインアルゴリズムとして採用されることが多い．
- Gradient Boostingと呼ばれるアンサンブル手法を採用している（後述）
- **データ点について損失を小さくする方向（勾配）** を逐次的に学習していく
- 「**直列的**」に弱学習器を学習させていくので，他のアンサンブル手法（e.g. Random Forest）と比較して学習時間が長くなる傾向がある
- 他の呼称がいくつか存在する
- GBM: Gradient Boosting Machine ← 汎用性をアピールか？
- MART: Multiple Additive Regression Tree ← IR系はこの呼び方が多い

### Motivation
- 強力なアルゴリズムなので，分散ノード上で動作し==非常に大きなサイズのデータセットを扱う==ことができるようになったら最強じゃないか？
- 直列的な学習を少しでも==高速化==することができればもっと良さそうじゃないか？

---

### REVIEW: Regression Tree

#### Notation
- データセット: $\mathcal{D}=\{\left(x^{(i)}, y^{(i)}\right)\}$
- 右肩の添字はデータ点のインデクサ
- $\left(x^{(i)}, y^{(j)}\right)$の組をデータ点と呼ぶ
- $i=1,\ldots,m$の$m$個のデータ点を含む
- 特徴量ベクトル: $x^{(i)} \in \mathbb{R}^{d}$
- $d$次元のベクトルで表現される
- $j$次元目の要素は$x^{(i)}_{j}$のように表現される（$j=1,\ldots,d$）
- 教師ラベル: $y^{(i)} \in \mathbb{R}$

#### データ点の2分
次元のインデクサ$j$について，$x^{(i)}_{j} \leq t$となるようなデータ点の集合を$L$，残りのデータ点の集合を$R$と表現する時，次の情報量$S_{j}$を最小にするような閾値$t$を求める．

$$
\begin{equation}
S_{j} \equiv \sum_{l \in L}\left(y^{(l)}-\mu_{L}\right)^{2}+\sum_{r \in R}\left(y^{(r)}-\mu_{R}\right)^{2}
\end{equation}
$$

ただし，$\mu_{L}, \mu_{R}$はそれぞれのデータ点集合の教師ラベルの平均値である．

==**POINT**== $t$の値の候補は$j$次元目の特徴量のユニークな値集合となる．

$S_{j}$をすべての取りうる$j$についてそれぞれ計算し，それが最小となるような$j$と，それに対応する$t$を利用してツリーのノードを分割していく．

#### ツリーの成長の停止条件
- リーフノードの数が$L$になる（$L-1$回の分割が必要になる）
- これ以上分割しても親ノードの$S$の値よりも小さくならない
- （設定した最大の深さに到達する）
- （リーフノードに属するデータ点の数が最小値以下になる）

#### リーフノードの出力
データ点一つの最終的な予測値は，そのデータ点が流れ着く先のリーフノードに属するデータ点の教師ラベルの平均値となる．


---

### REVIEW: Gradient Boosting Regression Tree
> ひとつひとつの弱学習器となる回帰木のことをStump（切株）と呼ぶらしい，素敵．

#### Notation
| Symbol | Description |
|:-------|:------------|
| $N$ | 弱学習器の数 |
| $\gamma_{kn}$ | $n$個目の回帰木の$k$番目のリーフノードの出力 |
| $\eta \gt 0$ | $\gamma_{kn}$に対する学習率．各リーフノードの出力に乗じる |
| $L_{n}$ | $n$個目の回帰木の$k$番目のリーフノードの数 |
| $f_{n}\left(x\right) \in \mathbb{R}$ | $n$個目の回帰木の出力 |
| $\alpha_{n} \in \mathbb{R}$ | $n$個目の回帰木の出力への重み |
| $F_{N}\left(x\right) \in \mathbb{R}$ | アンサンブル結果の最終的なモデル |

#### 最終的なモデルの出力
$$
F_{N}\left(x\right) = \sum_{n=1}^{N}\alpha_{n}f_{n}\left(x\right)
$$


#### 弱学習器の学習
> $n$個の回帰木が学習されたその次のものはどのように学習されるのか？

$C$を損失とする時，これは$F_{n}$の関数であるから$C\left(F_{n}\right)$と表現できる．$\delta$を微小な差分を取る演算子とすると，損失とモデルの出力の間には次のような近似式が成立する．

$$
\begin{equation}
\delta C \approx \frac{\partial C\left(F_{n}\right)}{\partial F_{n}} \delta F
\end{equation}
$$

この式が意味するところは，$\delta F = - \eta \frac{\partial C}{\partial F_{n}}$とおいてやることで，損失を小さくする方向（$\text{i.e.}$ $\delta C \lt 0$）に近づけていくことが可能ということ（∵ $\eta \gt 0$かつ$\left(\frac{\partial C}{\partial F_{n}}\right)^{2} \gt 0$　が成立する）．

$n$個目の弱学習器が予測すべき値としてこの値を設定してやれば，学習器を積み重ねていくにつれて全体の損失が逐次的に小さくなっていく（Boostingされていく）．つまり，$n$個目の決定木の$k$番目のリーフノードの出力$\gamma_{kn}$が$-\frac{\partial C}{\partial F_{n}}$となるように学習させていけば良い．

$\eta$を小さい値に設定すれば過学習を防ぐことにつながる（$\text{i.e.}$ Trainに適合しすぎない）．

:::info
GBRTは関数出力の空間において勾配降下法を利用しているとみなすことができる．
個々の回帰木は二乗損失を最小にするように最適化されていくが，全体では分類やランキングといった他のタスクを解くように最適化していくことが可能．
:::

#### 弱学習器の学習のイメージ図
- $-\frac{\partial C}{\partial F_{n}}$ は`Pseudo Residuals`と呼ばれたりもする．


#### 弱学習器の線形結合の重み
つまり$\alpha_{n}$の最適化．損失関数$C$について$\alpha$を動かして小さくなるように探索すれば良い（参考資料によると$1$次元の最適化問題とのこと）．

$$
\alpha_{n}=\underset{\alpha}{\arg \min } \sum_{i=1}^{m} C\left(y^{(i)}, F_{n-1}\left(x^{(i)}\right)+\alpha f_{n}\left(x^{(i)}\right)\right)
$$

##### この問題が解けることの証明？
有限個の閉集合


---

### 学習の並列化
これまでに紹介した通り，GBRTは逐次的に弱学習器を学習していくので，Random Forestのような並列した弱学習器の獲得ができない．したがって，ここでの高速化は決定木の構築の並列化に限定される．

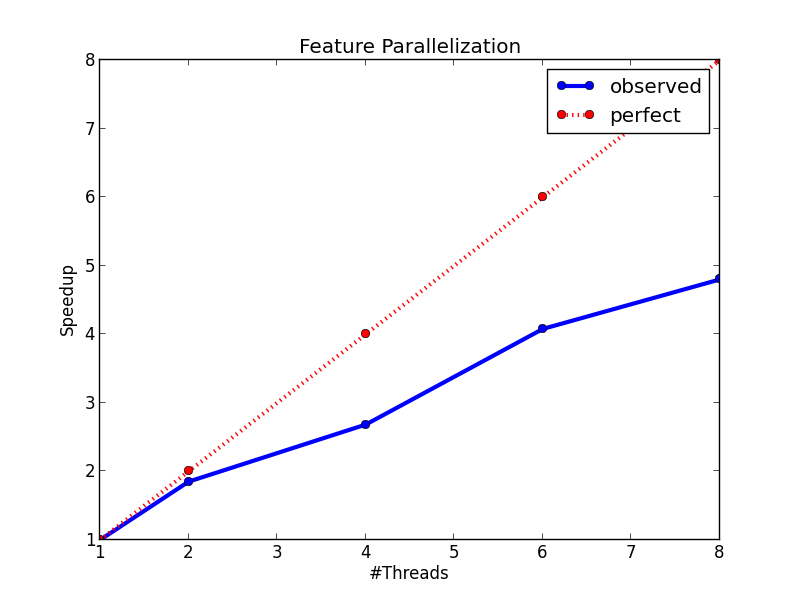
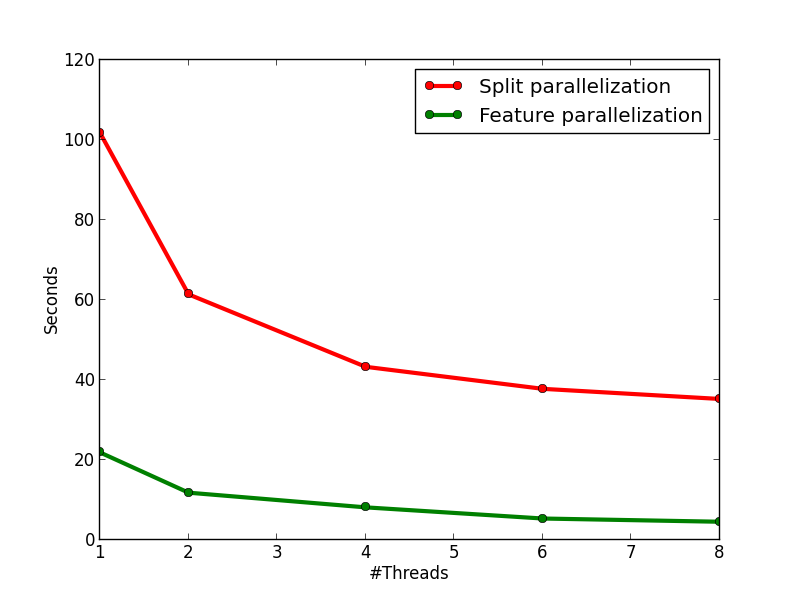
#### 結果
- ３種類の並列化の手法を提案
- OpenCVやXGBoostの実装よりも高速に動作
- 精度については同じくらいとのこと


:::info
実験の条件は以下の通り．
##### 実行環境
- メモリ: 64GB
- OS: Debian
- CPUs: 8 Intel E5-2650 2.0GHz

##### ハイパーパラメータ
- $N=100$
- $\text{max_depth}=8$
- $\text{min_samples_per_node}=10$

##### データセット
- small: (130K, 42)
- large: (1M, 42)
:::

#### :cry: Method 1: （Node Parallelization）ノード生成の並列化
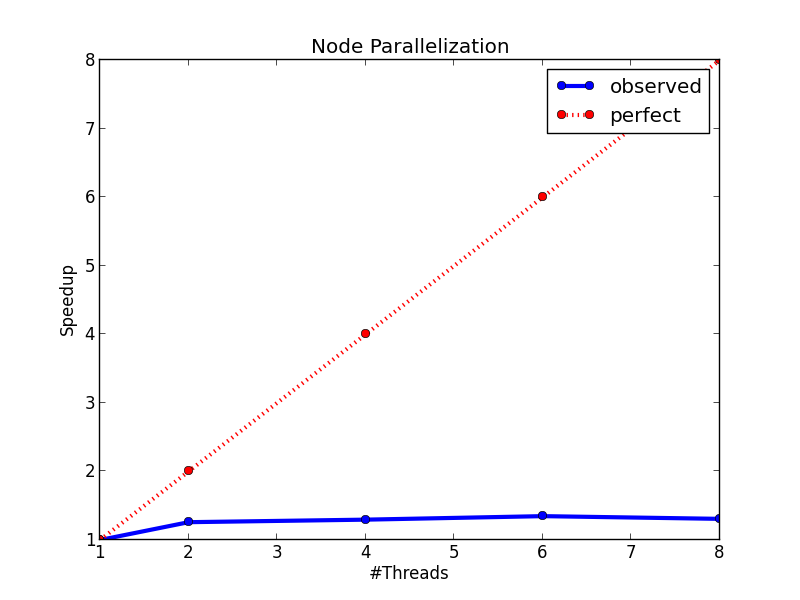
それぞれのレベルで**ノードの生成を並列化**する試み．
分割そのものを各スレッドが実行するということ．

→ **workload imbalanced**問題が起きうる．

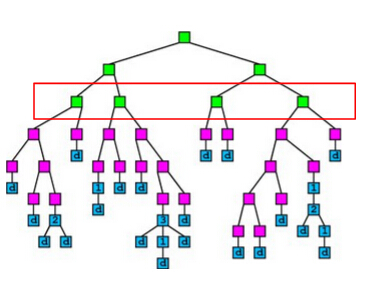
各ノードは互いに似通ったデータ点の集合となりやすいため．
データ点の集合は均一ではなく偏っていることがほとんどであるので，分割後のノードに属するデータ点集合のサイズが不均一になり，効率的な並列化ができないということ．

具体例は以下の図のような状況．（赤枠の左から）１，３番目のノードは他のものと比較してサイズが小さいことがわかる．

<div>


</div>

---

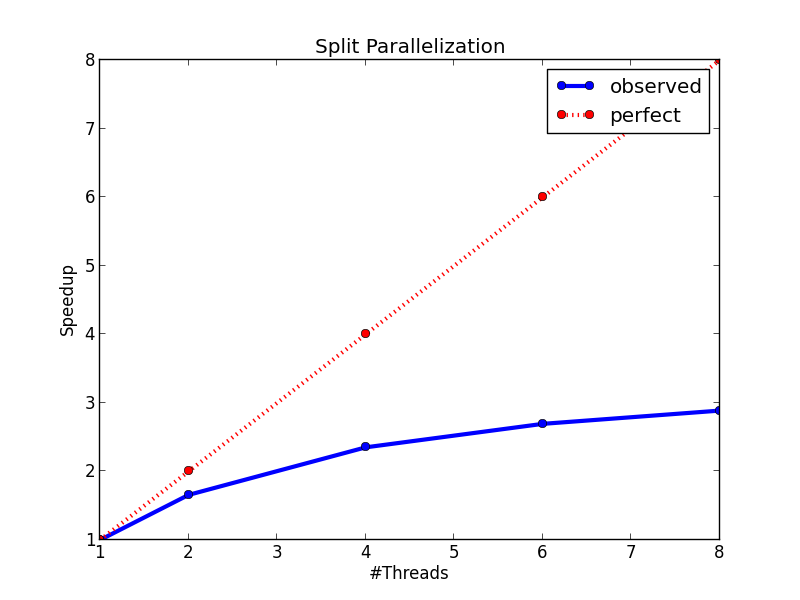
#### :sweat_smile: Method 2: （Split Parallelization）ノードレベルでの分割の閾値探索の並列化
[これまでの説明](#データ点の2分)での閾値$t$の探索を並列化する試み．
ノードに属するデータ点のサイズが大きいうちには探索のコストがある程度大きいので並列化そのもののオーバーヘッドを無視できる程度に並列化の恩恵が得られるが，木が深くなるにつれてサイズが小さくなり，オーバーヘッドが目立ってしまう．

→ 上述の手法よりは高速化されるが，それでも（理想的な）ピークの半分程度の高速化しか達成できない．

$j=1,\ldots,d$について最適な閾値の探索を行う際に，$d$回行われる線形探索をスレッドベースで高速化する方法．

---

#### :sunglasses: Remark 3: （Feature Parallelization） 特徴量ごとの閾値探索の並列化
> 結局ソートのコストが高いだけだったのでは？

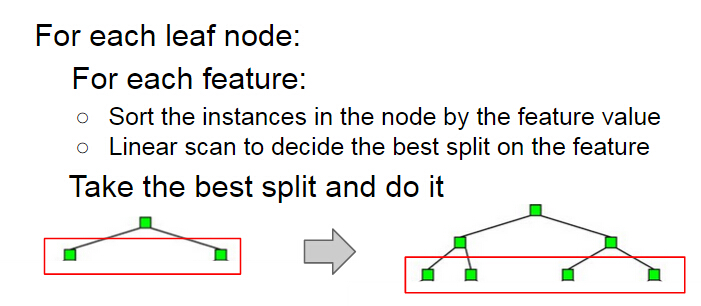
ループの順番を入れ替えて，ソートするコストを削減する試み．最初にすべての特徴量次元についてデータ点集合を並び替えた結果を保持しておき，各探索時にその情報を利用するというもの．

各スレッドは閾値の線形探索時に各リーフノードの*scanning status*を注意深く管理する必要がある．

- **並列化のオーバーヘッドが小さい**
- **各スレッドの負荷が均等になる**: 特徴量に関係なくデータ点集合のサイズが均等なので，各スレッドのジョブの負荷が同程度になる．

##### ==Before==
<div style="max-width: 60%;">


</div>

##### ==After==
<div style="max-width: 60%;">


</div>

---

#### Results
<div style="display: flex; max-width: 100%;">
<div>

</div>
<div>

</div>
</div>
<div style="display: flex; max-width: 100%;">
<div>

</div>
<div>

</div>
</div>

#### WIP その先へ
SparkTreeの実装の解説（section 4あたりのお話を）

### Implementations
| Package | Pros | Cons |
|:--------|:-----|:-----|
| [scikit-learn](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html) | おなじみ | 並列実装がない（気がする） |
| [XGBoost](https://github.com/dmlc/xgboost) | | |
| [lightGBM](https://github.com/microsoft/LightGBM) | | |
| [CatBoost](https://github.com/catboost/catboost) | 最強[らしい](https://catboost.ai/#benchmark) | |

## Factorization Machines

### Goals
- FMsの強みがわかる
- スパース特徴量の交互作用を考慮できる
- 潜在ベクトルの次元数$k$と特徴量次元数$d$について推論に$O\left(kn\right)$で済む

### Useful links
- [Factorization Machines](https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf) by S. Rendle
- [時間計算量が各変数について線形で済むことの証明のメモ](https://hackmd.io/@moriaki3193/r1NxQZwbr) ← WIP
- 派生モデルをまとめたもの．
- [incremental FMsまとめてみた](https://hackmd.io/@moriaki3193/rk5Iz2NxV)
- [Bayesian FMsまとめてみた](https://hackmd.io/@moriaki3193/r1uonFEgN)
- [ridge](https://github.com/moriaki3193/ridge) ← 昔実装したパッケージ
- PyPIで入る（はず）
- [Rustで実装したやつ](https://github.com/moriaki3193/spike/blob/master/src/fm.rs)

### Motivation
- SVMsやDNN系のモデルがうまく推定できない，スパースデータにおける交互作用の推定が得意
- FMsの出力の式はパラメータについて線形の時間計算量で済む．大規模なデータセットでも学習&推論可能
- スパースな特徴量ベクトルに限らず，一般的な実ベクトルを入力にとって動作する
- 分類・ランキング学習といったタスクにも応用例が豊富にある

### 問題設定

### モデル式
$$
\hat{y}(\mathbf{x}) :=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j}
$$

#### Parameters
$$
w_{0} \in \mathbb{R}, \quad \mathbf{w} \in \mathbb{R}^{n}, \quad \mathbf{V} \in \mathbb{R}^{n \times k}
$$

- $k$はハイパーパラメータ
- 十分に大きく取れば，もとのデータ点を表現できる

#### 線形性の証明（$d=2$）
$$
\begin{aligned} & \sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j} \\=& \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j}-\frac{1}{2} \sum_{i=1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{i}\right\rangle x_{i} x_{i} \\=& \frac{1}{2}\left(\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{f=1}^{k} v_{i, f} v_{j, f} x_{i} x_{j}-\sum_{i=1}^{n} \sum_{f=1}^{k} v_{i, f} v_{i, f} x_{i} x_{i}\right) \\=& \frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)\left(\sum_{j=1}^{n} v_{j, f} x_{j}\right)-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right) \\=& \frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right) \end{aligned}
$$

#### 出力に対する微分係数
$$
\frac{\partial}{\partial \theta} \hat{y}(\mathbf{x})=\left\{\begin{array}{ll}{1,} & {\text { if } \theta \text { is } w_{0}} \\ {x_{i},} & {\text { if } \theta \text { is } w_{i}} \\ {x_{i} \sum_{j=1}^{n} v_{j, f} x_{j}-v_{i, f} x_{i}^{2},} & {\text { if } \theta \text { is } v_{i, f}}\end{array}\right.
$$

## Gradient Boosting Factorization Machines
Factorization Machinesの手法に**Gradient Boosting**の手法を応用したもの。
~~分類・ランキングの問題へのFMsの応用という立ち位置よりは、学習の手法としてアンサンブルの考え方を導入したものとして位置付けることができそう。~~
全ての特徴量間の交互作用を学習しようとするFMsの手法に対し、「本当に効いている」交互作用を抽出して学習させる工夫を導入した点が面白い。

この手法をよりランキングの問題よりに拡張した手法として**BoostFM**が存在する。

この論文は[ここ](http://tongzhang-ml.org/papers/recsys14-fm.pdf)から読むことができる．

### Abst.
推薦の問題において、FMsは**context-aware**な手法であり有用であることが示されてきた。これは、ユーザ・アイテムのレーティング行列の次元削減だけではなく、補助的な**context**を考慮できることを指している。しかし、この論文では、以下のように主張する。

> In practice, there are tens of context features and not all the pair- wise feature interactions are useful.

つまり、FMsでは**全ての(pairwiseな)特徴量どうしの交互作用を考慮する**ため、不必要な交互作用項までモデルに影響を与えているということである。
しかし、前もってある交互作用が必要かどうかなどわからないから、学習の段階でなんとか工夫してやりたいという**気持ち**が芽生えるわけである。

### Intro.
この論文の立ち位置は基本的に...
> Thus it is challenging to automati- cally select useful interaction features to reduce noise

というもの。
これまでに**Matrix Factorization**においてGradient Boostingの手法を導入したものとして次の論文を取り上げている。

- General functional matrix factorization using gradient boosting(2013)

しかし今回の論文での主目的は**有用な交互作用を自動的に選択する**ことであり、そのための方法として**Greedyに有用な交互作用を抽出し、現時点でのモデルの残渣を小さくするようにその交互作用を与える潜在ベクトルを追加学習する**ことを提案している。

#### この論文の新規性
- FMsの手法と比較して、ノイズを削減することが可能な手法としてGradient Boostingを利用した、交互作用の効率的な選択アルゴリズムの提案
- **GBFM**が推薦のための回帰問題だけではなく、様々な問題に応用できる汎用的なフレームワークであることを提示
- 提案手法がこれまでの手法よりも優れていることを定量的に説明

### 関連研究
#### Matrix Factorization
MFについて、レーティング行列の次元削減の箇所ばかりに触れてきたが、統計的にどのような解釈がなされるかについての説明があったので、簡単にまとめる。

##### レーティング行列の生成
あるユーザ$i$のあるアイテム$j$に対する評価を$R_{ij}$とする。
この時、$R_{ij}$は平均$U_{i}V_{j}^{T}$標準偏差$\sigma_{R}$の正規分布にしたがって生成されると仮定する。
この仮定を置く時、あるレーティング行列が得られる確率は次のように表現される。

$$
p ( R | U , V , \sigma _ { R } ^ { 2 } ) = \prod _ { i = 1 } ^ { m } \prod _ { j = 1 } ^ { n } \left[ \mathcal { N } \left( R _ { i j } | U _ { i } V _ { j } ^ { T } , \sigma _ { R } ^ { 2 } \right) \right] ^ { I _ { i j } ^ { R } }
$$

ただし、$I_{ij}^{R}$はなんらか評価が与えられている場合に$1$、そうでなければ$0$となるようなインジケータ関数であり、単に$0$であれば累乗した結果が$1$となるから、尤度に影響を与えないというだけの話。

また、$U$と$V$の各要素は平均$0$標準偏差$\sigma_{U}, \sigma_{V}$の球面ガウス分布に従うという事前分布を置く。

$$
p ( U | \sigma _ { U } ^ { 2 } ) = \prod _ { i = 1 } ^ { m } \mathcal { N } \left( U _ { i } | 0 , \sigma _ { U } ^ { 2 } \boldsymbol { I } \right) , p ( V | \sigma _ { V } ^ { 2 } ) = \prod _ { j = 1 } ^ { n } \mathcal { N } \left( V _ { j } | 0 , \sigma _ { V } ^ { 2 } \boldsymbol { I } \right)
$$

ベイズ推論を行うと、結局次のような目的関数を最小にするようなパラメータの推定結果が得られるという流れ。

$$
\min _ { U , V } \frac { 1 } { 2 } \sum _ { i = 1 } ^ { m } \sum _ { j = 1 } ^ { n } I _ { i j } ^ { R } \left( R _ { i j } - U _ { i } V _ { j } ^ { T } \right) ^ { 2 } + \frac { \lambda _ { 1 } } { 2 } \| U \| _ { F } ^ { 2 } + \frac { \lambda _ { 2 } } { 2 } \| V \| _ { F } ^ { 2 }
$$

この目的関数はSGDやALSといった手法で最適化できる。

結局今までMFで解いていたのは、統計的に解釈するとこのような仮定とモデリングの上に成り立っているということが理解できよう。

#### Context-aware recommendation

$$
\begin{aligned} \mathcal { U } & = \left\{ u _ { 1 } , u _ { 2 } , u _ { 3 } \right\} \\ \mathcal { I } & = \left\{ i _ { 1 } , i _ { 2 } , i _ { 3 } , i _ { 4 } \right\} \\ \mathcal { M } & = \{ \text{Happy}, \text {Normal}, \text {Sad} \} \end{aligned}
$$

Matrix Factorizationの手法では、ユーザとアイテムのIDのみを利用していたが、Factorization Machinesは補助的な情報を考慮できる。
「補助的な情報」とは、カテゴリカルな変数であったり、連続値の変数であってもよい。

ユーザ・アイテム・$m - 2$個の変数をモデルの入力ベクトルに落とし込む。
ユーザもアイテムも実際には離散的な変数として解釈できるから、$m$個のカテゴリカル変数を考えていることになる。
それぞれの変数を$C_{i}$、その変数の定義域を$n_{i}$と表現する。
この時、入力ベクトルの次元数は$\sum_{i}^{m}n_{i}$となる。
データセット$\sum_{i}^{N}\left(\mathbf{x_{i}}, y_{i}\right)$が得られた時のモデルの学習は次のような問題を解くことに相当する。

$$
\hat { y } : \mathbb { R } ^ { d } \rightarrow \mathbb { R }
$$

パラメータの推定は、次のような最小化問題の解として与えられることになる。
ただし、$l$は（パラメータについて）微分可能な凸な損失関数であり、$\Omega$はモデルの複雑さを表現する関数で過学習を防ぐ目的で設定される。

$$
\underset { \Theta } { \arg \min } \sum _ { i = 1 } ^ { N } l \left( \hat { y } _ { i } , y _ { i } \right) + \Omega ( \hat { y } )
$$

### GBFM
#### Gradient Boosting
$$
\hat { y } _ { s } ( \mathbf { x } ) : = \hat { y } _ { s - 1 } ( \mathbf { x } ) + \sum _ { i \in \mathcal { C } _ { p } } \sum _ { j \in \mathcal { C } _ { q } } \mathbb { I } [ i , j \in \mathbf { x } ] \left\langle \mathbf { V } _ { p } ^ { i } , \mathbf { V } _ { q } ^ { j } \right\rangle
$$


#### Greedy Feature Selection Algorithm