# 2022q1 Homework2 (quiz2)
contributed by < [`meyr`](https://github.com/meyr) >
題目:[2022q1 quiz2](https://hackmd.io/@sysprog/linux2022-quiz2)
作業區 :[2022q1 homework](https://hackmd.io/@sysprog/linux2022-homework2)
## 測驗 1
### 1. 解釋程式碼運作的原理
個無號整數取平均值的程式碼。
```c=
#include <stdint.h>
uint32_t average(uint32_t a, uint32_t b)
{
return (a + b) / 2;
}
```
觀察不同數值的結果,因為程式碼有除以2,==等於是無條件捨去。==
| | floating | average() |
| -------- | -------- | -------- |
| $(2 + 3)/2$ | $2.5$ | $2$ |
| $(2 + 4)/2$ | $3.0$ | $3$ |
| $(3 + 3)/2$ | $3.0$ | $3$ |
所以我們改寫成以下等價的實作時,
```c=
#include <stdint.h>
uint32_t average(uint32_t a, uint32_t b)
{
return (a >> 1) + (b >> 1) + (EXP1);
}
```
因為 (a >> 1) 會損失LSB一個bit,所以我們必須對兩個數的LSB做判斷。
| | 判斷式 | |
| -------- | -------- | -------- |
| 無條件捨去 | (a & 1) && (b & 1) | 當a和b的最後一個bit都是1才進位 |
| 無條件進位 | (a & 1) \|\| (b & 1)| 當a或b的最後一個bit是1才進位
| 四捨五入 | (a & 1) \|\| (b & 1)| 因為0.5就進位和無條件進位一樣
這邊使用無條件捨去,所以只需要判斷a和b的LSB是否同時為1。
```c
(a & 1) && (b & 1)
```
可以簡化為
```c
a & b & 1
```
:::info
如果是數值分析,或是其他對數值敏感的應用,因為這個程式碼是無條件捨去,等於是有個DC offset。多次使用會讓值域越來越小。
:::
另外 a+b可以寫成下面的程式碼
```c=
(a & b) << 1 + (a ^ b)
```
其中a & b為carry,當兩個數都為1才需要進位。
其中a ^ b為sum,當只有一個為1才是1,否則為0。
所以
```c=
((a & b) << 1 + (a ^ b)) >> 1
```
可以簡化為
```c=
(a & b) + (a ^ b) >> 1
```
### 3.Exponentially weighted moving average (EWMA)
在kernel中有個header [include/linux/average.h](https://github.com/torvalds/linux/blob/master/include/linux/average.h)定義了EWMA。參考[wiki](https://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average)的解釋

當t = 0時,第一筆data為Y[0]即為輸出的S[0] = Y[0]。
當t = 1時,第二筆data為Y[1],則輸出為S[1] = a * Y[1] + (1 - a) * S[0]。
當t = 2時,第三筆data為Y[2],則輸出為S[2] = a * Y[2] + (1 - a) * S[1]
也就是當前的資料給一個weight alpha,其他資料就是給(1 - alpha)的weight,可以展開成以下的式子。
$$
S[N] = \alpha Y[N] + \alpha (1-\alpha)Y[N - 1] + \alpha(1 - \alpha)^2 * Y[N - 2] + ...
$$
當alpha小於1,則(1 - alpha) < 1,也就是越前面的資料影響越小。
#### Alpha的選擇
ref1 : [Exponential Moving Average](https://tttapa.github.io/Pages/Mathematics/Systems-and-Control-Theory/Digital-filters/Exponential%20Moving%20Average/Exponential-Moving-Average.html)
ref2 : [Frequency Response of the Running Average Filter](https://ptolemy.berkeley.edu/eecs20/week12/freqResponseRA.html)
這個式子是一個==IIR的Low pass filter架構==。因為是lowpass filter,所以可以得出DC值,而DC值就是數值的平均值。
其中frequency response如下圖所示。可以看出確實是一個lowpass filter。
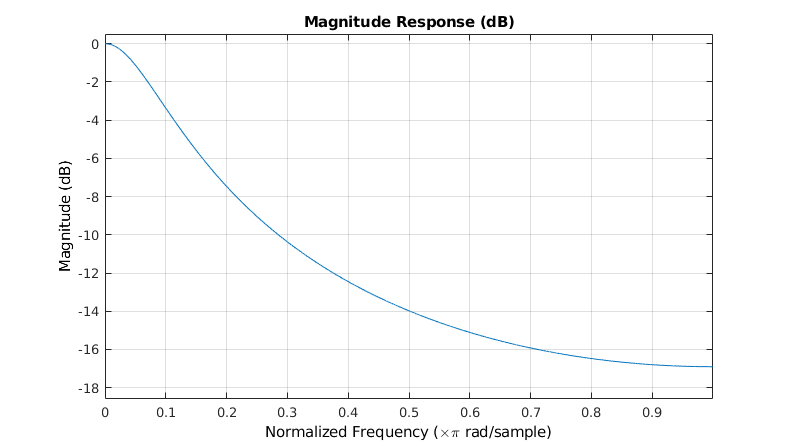
另外不同的$\alpha$也會對frequency response產生影響,造成lowpass filter的passband的頻寬大小不一樣。如下圖所示。
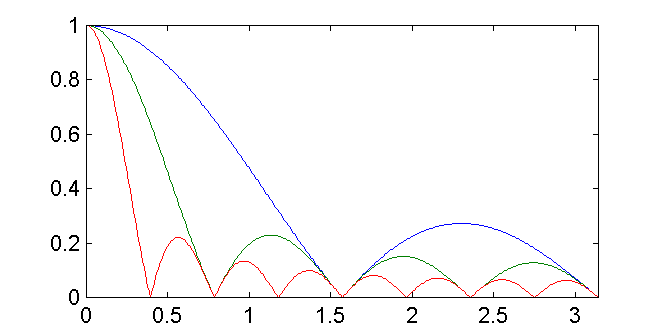
| | $\alpha$數值 | 頻寬 | 取得正確平均的時間 | 受noise的影響 |
| ------------ | ------------ | --- | ------------------ | ------------- |
| $\alpha$越小 | $1\over64$ | 越小 | 越慢 | 越小 |
| $\alpha$越大 | $1\over4$ | 越大 | 越快 | 越大 |
#### 名詞解釋
| Funciton Name | Description |
| ---------------------- | -------------------------- |
| **BUILD_BUG_ON(cond)** | 停止compile如果cond是true. |
|**BUILD_BUG_ON_NOT_POWER_OF_2(var)** | 停止compile如果var不是2的次方。
|**__builtin_constant_p(var)** | 判斷var是否為常數,返回1為常數,返回0則否。
|**READ_ONCE/WRITE_ONCE** | 參考[這裡](/YcjVoBx5R_mnKxX9-H6pEg#READ_ONCEWRITE_ONCE)</br>就是volatile的封裝。當需要用的時候把變數轉換成volatile型態,編譯器只是保證 2 個 volatile 變數之間讀取不會被亂序。
#### Source Code分析
從[LXR](https://elixir.bootlin.com/linux/latest/source)中找出使用EWMA的例子[sta_info.h](https://elixir.bootlin.com/linux/latest/source/net/mac80211/sta_info.h#L126),
其中第一個為name,第二個為pricision,第三個alpha值。
因為alpha為小於1的值,所以這個為$\alpha = 1 / 8$。
```c=
DECLARE_EWMA(avg_signal, 10, 8)
```
另外一個很重要的變數==weight_rcp,就是把輸入的8取log2。==
```c=
unsigned long weight_rcp = ilog2(_weight_rcp);
```
根據ilog2的定義。[include/linux/log2.h](https://github.com/torvalds/linux/blob/master/include/linux/log2.h#L77),因為我們限制_weight_rcp一定要為2的次方,所以log2(_weight_rcp)就是==找出MSB的位數==。這樣我們做乘法或是除法的時候只需要用shift就可以達成。
例如:
ilog2(8) = 3
ilog2(16) = 4
ilog2(32) = 5
重點是怎麼把val加進來,所以只分析這個function。
```c=
WRITE_ONCE(e->internal, internal ?
(((internal << weight_rcp) - internal) +
(val << precision)) >> weight_rcp :
(val << precision));
```
根據上面的邏輯重新改寫。
```c=
if(internal) // 第一筆,直接放入
e->internal = val << precision;
else { // 第二筆之後
unsigned long newdata = val << precision;
unsigned long olddata =
(internal << weight_rcp) - internal;
e->internal = (olddata + newdata) >> weight_rcp;
}
```
原本的算式
$$
S[N] = \alpha*Y[n] + (1-\alpha)*S[N-1]
$$
把$\alpha$提出到式子外面。
$$
S[N] = \alpha(Y[N] + ({1\over\alpha} - 1)*S[N - 1])
$$
最後等於下面的算式
$$
S[N] = \alpha(Y[N] + {1\over\alpha}*S[N-1] - S[N - 1])
$$
因為$\alpha$小於1,所以**乘於$\alpha$等於向右shift(>> weight_rcp)**
**乘於$1\over\alpha$等於向左shift(<< weight_rcp)。**
#### 在 Linux 核心的應用
通常是計算平均成的場合使用。每一筆資料近來,我就可以算出平均值,而不用儲存以前的數值。參考以下的程式碼[drm_self_refresh_helper.c:275](https://elixir.bootlin.com/linux/latest/source/drivers/gpu/drm/drm_self_refresh_helper.c#L256)
==init之後,第一筆資料給有可能的平均值,可以快速得到準確的平均值,而不用從不正確的值慢慢收斂。==
```c=
#define SELF_REFRESH_AVG_SEED_MS 200
DECLARE_EWMA(psr_time, 4, 4)
ewma_psr_time_init(&sr_data->entry_avg_ms);
ewma_psr_time_init(&sr_data->exit_avg_ms);
/*
* Seed the averages so they're non-zero (and sufficiently large
* for even poorly performing panels). As time goes on, this will be
* averaged out and the values will trend to their true value.
*/
ewma_psr_time_add(&sr_data->entry_avg_ms, SELF_REFRESH_AVG_SEED_MS);
ewma_psr_time_add(&sr_data->exit_avg_ms, SELF_REFRESH_AVG_SEED_MS);
```
## 測驗 2
### 1.解釋程式碼運作的原理
實作branchless的max函數。
```c
#include <stdint.h>
uint32_t max(uint32_t a, uint32_t b)
{
return a ^ ((EXP4) & -(EXP5));
}
```
先觀察這個function,只知道a ^ (某個數)要得到我們的答案。
所以得到以下的table。
| input | expect | internal |
| ----- | ------ | -------- |
| a > b | a | a ^ 0 |
| a < b | b | a ^ (a ^ b)|
另外2的補數特性
| val | -val(10進位) | -val(2進位) |
| -------- | -------- | -------- |
| 1(true) | -1 | 1111...1111(全部為1) |
| 0(false) | 0 | 0000...0000(全部為0) |
所以
| expr | EXP3 == true | EXP3 == false|
| -------- | -------- | -------- |
| (EXP4) & -(EXP3) | EXP4 | 0 |
所以我們可以用以下來實現max
```c
#include <stdint.h>
uint32_t max(uint32_t a, uint32_t b)
{
return a ^ ((a ^ b) & -(a < b));
}
```
### 3.在 Linux 核心原始程式碼中,找出更多類似的實作手法
```c
if (i & lsbit)
i -= size;
```
下面的程式碼是實作上面的branchless的等校程式碼。
```c
i -= size & -(i & lsbit);
```
如同上面分析的,
| expr | i & lsbit == 1 | i & lsbit == 0|
| -------- | -------- | -------- |
| (size) & -(i & lsbit) | size | 0 |
## 測驗7
FizzBuzz的題目為,當數字為3的倍數則印出"Fizz",當數字為5的倍數則印出"Buzz",如果同時是3和5的倍數則印出"FizzBuzz"。
老師給的程式碼如下:
```c
#include <stdio.h>
int main() {
for (unsigned int i = 1; i < 100; i++) {
if (i % 3 == 0) printf("Fizz");
if (i % 5 == 0) printf("Buzz");
if (i % 15 == 0) printf("FizzBuzz");
if ((i % 3) && (i % 5)) printf("%u", i);
printf("\n");
}
return 0;
}
```
這邊應該要把i % 15的順序排在最上面,不然沒機會印出"FizzBuzz",所以修改程式碼如下:
```c
#include <stdio.h>
int main() {
for (unsigned int i = 1; i < 100; i++) {
if ((i % 3 == 0) && (i % 5 == 0)) printf("FizzBuzz\n");
else if (i % 3 == 0) printf("Fizz\n");
else if (i % 5 == 0) printf("Buzz\n");
else printf("%u\n", i);
}
return 0;
}
```
另外列印字串的程式改用以下的方法
```c
char fmt[9];
strncpy(fmt, &"FizzBuzz%u"[start], length);
fmt[length] = '\0';
printf(fmt, i);
printf("\n");
```
其中length為需要列印字串的長度
| length | M5 == 0 | M5 == 1 |
| -------- | -------- | -------- |
| M3 == 0 | 2(%u) | 4(Buzz) |
| M3 == 1 | 4(Fizz)| 8(FizzBuzz)|
所以 length可以用以下的方法算得
```c
unsigned int length = (2 << div3) << div5;
```
另外字串是由"FizzBuzz%u"來取得,所以必須要有不同的offset。
| offset | M5 == 0 | M5 == 1 |
| -------- | -------- | -------- |
| M3 == 0 | 8(%u) | 4(Bizz) |
| M3 == 1 | 0(Fizz)| 0(FizzBuzz)|
所以offset可以由以下的程式碼算得
```c
unsigned int offset = (8 >> div5) >> (div3 << 2);
```
修正過的程式碼如下,可以正確的顯示FizzBuzz
```c=
uint8_t div3 = is_divisible(i, M3);
uint8_t div5 = is_divisible(i, M5);
unsigned int length = (2 << div3) << div5;
unsigned int offset = (8 >> div5) >> (div3 << 2);
char fmt[9];
strncpy(fmt, &"FizzBuzz%u"[offset], length);
fmt[length] = '\0';
printf(fmt, i);
printf("\n");
```
###### tags: `linux2022`
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet