# Recurrent Neural Networks

## 1. Time Series Features

Consider a sentence as follows :

*He is a teacher. She is a student.*

How do we extract the features from this sentence ?

### 1.1 Sentence-level Features
- Extract features from each sentence :
- Bag-of-words

1. Build a list contain all words of the sentence:
[ "he", "she", "is", "a", "teacher", "student" ]

2. Generate a vector which length is the same as length of the list:
[ 0, 0, 0, 0, 0, 0]

3. Replace zero with word frequency :
[ 1, 1, 2, 2, 1, 1 ]

- Advantage :
- It can fit the most of machine learning model.

- Disadvantage :
- Loss the information of relation between words.
- *He is a teacher. She is a student.*
- *He is a student. She is a teacher.*

### 1.2 Word-level Features

- Extract features from each word
- One-hot
- Word embedding
- embedding layer
- word2vec
- Word-level features will contain 2 domains:
- Time domain and word domain.
- For example, we can get the features as follows by one-hot encoding :
[[1, 0, 0, 0, 0, 0], => He
[0, 0, 1, 0, 0, 0], => is
[0, 0, 0, 1, 0, 0], => a
[0, 0, 0, 0, 1, 0], => teacher
[0, 1, 0, 0, 0, 0], => She
[0, 0, 1, 0, 0, 0], => is
[0, 0, 0, 1, 0, 0], => a
[0, 0, 0, 0, 0, 1]] => student
- We can flatten the features to a vector and feed it to maching learning model.
- But the model still **cannot** learn the relation between words.

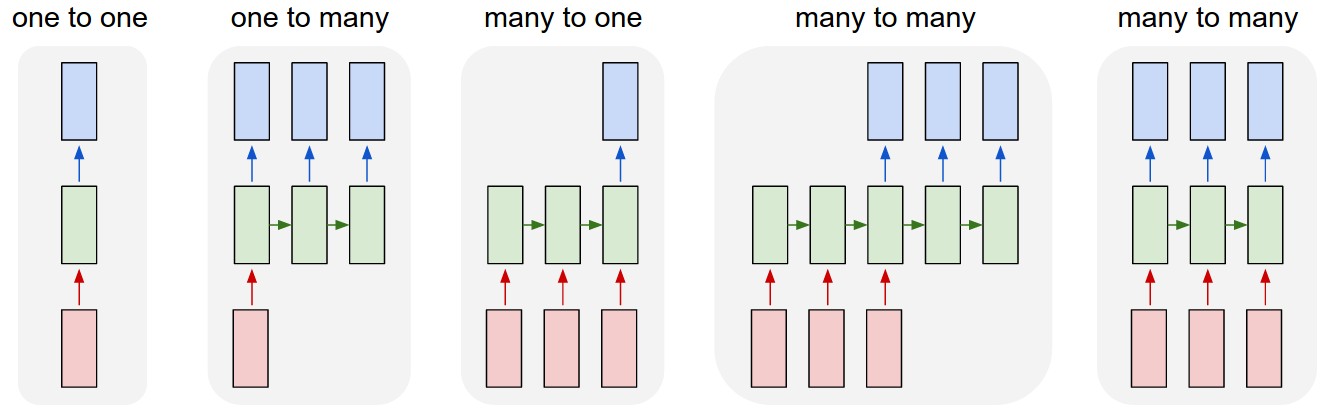
## 2. Recurrent Neural Networks

### 2.1 Basic Architecture

Idea: feed a word and a previous state to machine learning model each time.

The model has two output: one for prediction and another for **hidden state**.


If we want to classify a sentence, we can treat the last output as prediction.
- Ignore intermediate output.

### 2.2 Backpropagation Through Time

In this architecture, backpropagation is not enough.
- Because we cannot optimize intermediate output.

Solution: recurrent neural network is a cyclic graph. Maybe we can simplify the architecture of recurrent neural network.


Here, Model 1, Model 2, ..., Model $n$ share the same weights and bias.

We can treat those models as a large, sequential model.
- $h_n$ is the output of this model.
- Ignore $h_1, h_2, ..., h_{n-1}$

Now, we can use backpropagation calculate the gradients easily.

Work flow of backpropagation through time:
1. Unroll the recurrent neural network.
2. Calculate the gradients of all trainable variables.
3. Roll-up the recurrent neural network.
4. Update trainable variables.

## 3. Long Short-Term Memory (LSTM)

### 3.1 Introduction

Reference: [Understanding LSTM Networks](http://colah.github.io/posts/2015-08-Understanding-LSTMs/)

#### Disadvantages of recurrent neural networks :
1. Gradient vanish
2. Gradient explode
3. Performance will be bad if time series is too long

#### Solution:
1. An additional new state: **cell state**
2. Three gates: **input gate**, **forget gate**, **output gate**

#### Simple work flow :
||time step 1|time step 2|time step 3|time step 4|time step 5|
|:------:|:--:|:--:|:--:|:--:|:--:|
|$x_t$ |2 |-1 |1 |2 |-1 |
|$x_{ti}$|999 |999 |-999|999 |999 |
|$x_{tf}$|999 |999 |999 |-999|-999|
|$x_{to}$|999 |-999|999 |999 |-999|
|C |2 |1 |1 |2 |-1 |
|h |2 |0 |1 |2 |0 |

Let
(1) $x_t$ is a word at time stamp $t$,
(2) $h_t$ is the hidden state at time stamp $t$,
(3) $C_t$ is the cell state at time stamp $t$.

Consider the current word and two previous states : $x_t, h_{t-1}, C_{t-1}$.
A LSTM cell calculates three values : $i_t, f_t, o_t$
Use those three values to generate next two states : $h_t, C_t$

#### Calculate $i_t$ (output of input gate) :

$$
i_t = Sigmoid(W_i \cdot [h_{t-1}, x_t] + b_i)
$$

#### Calculate $f_t$ (output of forget gate) :

$$
f_t = Sigmoid(W_f \cdot [h_{t-1}, x_t] + b_f)
$$

#### Calculate $o_t$ (output of output gate) :

$$
o_t = Sigmoid(W_o \cdot [h_{t-1}, x_t] + b_o)
$$

#### Calculate $C_t$ (cell state) :

$$
\bar C_t = tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \\
C_t = f_t * C_{t-1} + i_t * \bar C_t
$$

#### Calculate $h_t$ (hidden state) :

$$
h_t = o_t * tanh(C_t)
$$

### 3.2 Model Architecture


Here, we show a simple stacked LSTM model.

- $h_{11}, h_{12}, ..., h_{1n}$ , $h_{21}, h_{22}, ..., h_{2n}$, $h_{3n}$ are 1D vectors. They are hidden states of each time stamp.
- The first two LSTM layers **return all hidden states**. And the last LSTM layer **only return the final hidden state**.
- We will feed the final hidden state $h_{3n}$ to a neural network.

We can unroll this architecture as follows :


example:

model = Sequential()
model.add(LSTM(64, return_sequences=True))
model.add(LSTM(64, return_sequences=True))
model.add(LSTM(64))
model.add(Dense(32, activation='relu'))
model.add(Dense(1, activation='sigmoid'))

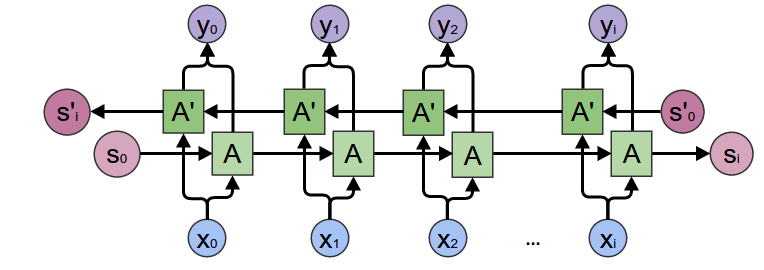
### 3.3 Bidirectional LSTM

A basic problem for all recurrent architectures:
- They will **forget** the features input at the beginning.
- This will be a problem if we pad all sequences to the same size.

For example, consider raw data as follows:
1. I am darby. I am handsome.
2. How are you?
3. To be or not to be, this is a question.

In practice, we will pad those sequences:
1. [pad] [pad] [pad] [pad] i am darby i am handsome
2. [pad] [pad] [pad] [pad] [pad] [pad] [pad] how are you
3. to be or not to be this is a question

#### Solution :
1. Reverse sequence order
2. Bidirectional LSTM


## 4. Sequence to Sequence Learning

Paper: [Sequence to Sequence Learning with Neural Networks](https://papers.nips.cc/paper/5346-sequence-to-sequence-learning-with-neural-networks.pdf)

Definition: feed a sequence to model and the model will response with a sequence, such as chatbot and machine translation.

- It is not a simple classification or regression model. Instead, it's a **generative model**.

### 4.1 Limitation of generative problem on a RNN model

Is it possible that we let each hidden states become an output sequence ?


- No, because we might need the whole input sequence to generate a response.


### 4.2 Encoder-Decoder Architecture

Idea: use a RNN model to encode the whole input sequence, and decode to a response by another RNN model.
- Sequence-to-sequence model (seq2seq)


1. For the encoder part, feed a whole input sequence to encoder model, and we will get a final cell state and hidden state.
2. For the decoder part, we **initialize** the decoder cell state and hidden state by the encoder cell state and hidden state.
3. Finally, we feed a **start token** to the decoder, and we can output a word.
- We feed this word to the decoder to get next word. Repeat this process until we get an **end token**.

### 4.3 Input and Output Encoding

Input: feel free to use any kind of word-level encoding method
- One-hot
- Word embedding (memory-friendly)

Output: only consider **one-hot** encoding.
- Seq2seq model will predict the class of each word.
- If the vocabulary size is 80000, the output layer of the decoder will have 80000 neurons.

Think: larger vocabulary size, more memory usage.

### 4.4 More Issues

- Optimize encoder: reverse sequence order.
- Optimize decoding process: beam search algorithm.

## 5. Attention Mechanism

Let's review seq2seq model :


For the first generated word "I", we can know that it is generated by token "[start]" with hidden state $h_0$ and cell state $C_0$.
- Also, $h_1$ and $C_1$ will be generated.

The second word "am" is generated by "I", $h_1$ and $C_1$.
- $h_2$ and $C_2$ will be generated, too.

Summary: $Word_t$ will be generated by $h_{t-1}$, $C_{t-1}$ and $Word_{t-1}$.
- $Word_t$ may depend on state $t-n$ or state $t+n$.
- Differnet words has different dependencies.
- For example, consider the following machine translation :
- I woke up at 8:00 a.m today. => 我今天早上8點起床
- The order of action and time is reverse. The second Chinese vocaulary "今天" depends on the final English word "today".

### 5.1 Architecture Overview


A new conception: **context vector**

### 5.2 Context Vector

Hidden states of encoder could be important.
- Generate a context vector which is a **weighted sum** of all hidden state of encoder.

Where are the weights of the weighted sum from?
- Based on **current hidden state of the decoder**.

Consider all hidden states of encoder $he_1, he_2, ... he_n$ and current hidden state of decoder $hd_t$. We can calculate their weights by the following equation:

$$
u^t_i = score(he_i, hd_t) \\
U^t = [u^t_1, u^t_2, u^t_3, ... u^t_n] \\
a^t = softmax(U^t) \\
c_t = \sum a^t_i \times he_i
$$

$score(.)$ is a function to calcuate the relation between $he_i$ and $hd_t$. For example:

$$
score(he_i, hd_t) = v^T tanh(W_e \cdot he_i + W_d \cdot hd_t)
$$

- $v^T$: a weight matrices
- $W_e, W_d$: trainable variables

### 5.3 Prediction

Prediction will be calculated by the **context vector** and **current hidden state of decoder**.

$$
\bar{hd}_t = tanh(W_c \cdot [c_t; hd_t]) \\
y_t = softmax(W_s \cdot \bar {hd}_t)
$$

## 6. More

- [Attention Is All You Need](https://arxiv.org/pdf/1706.03762.pdf)
- [BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding](https://arxiv.org/pdf/1810.04805.pdf) (and many other BERT-variants like ALBERT, RoBERTa, XLNet, ELECTRA ...)
- [Visualizing memorization in RNNs](https://distill.pub/2019/memorization-in-rnns/#appendix-autocomplete)
- Bistable Reccurent Cell (BRC, 2020) >> [A bio-inspired bistable recurrent cell allows for long-lasting memory](https://arxiv.org/pdf/2006.05252.pdf)

## Reference

- [A Gentle Introduction to Backpropagation Through Time](https://machinelearningmastery.com/gentle-introduction-backpropagation-time/)
- [Understanding LSTM Networks](http://colah.github.io/posts/2015-08-Understanding-LSTMs/)
- [Attention Mechanism(Seq2Seq)](https://www.slideshare.net/healess/attention-mechanismseq2seq)
- [Hierarchical Attention Networks for Document Classification](https://www.cs.cmu.edu/~diyiy/docs/naacl16.pdf)
- [Neural Machine Translation by Jointly Learning to Align and Translate](https://arxiv.org/pdf/1409.0473.pdf)
- [Understanding Bidirectional RNN in PyTorch](https://towardsdatascience.com/understanding-bidirectional-rnn-in-pytorch-5bd25a5dd66)
- [李宏毅 Transformer](http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2019/Lecture/Transformer%20(v5).pdf)
- [李宏毅 Structured Learning: Recurrent Neural Network](http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/RNN%20(v2).pdf)