---
tags: machine-learning
---

# Principal Component Analysis

<div style="text-align:center">
<img src="https://raw.githubusercontent.com/valoxe/image-storage-1/master/blog-machine-learning/principal-component-analysis/1.png" height="100%" width="70%">
</div>

> This is my personal notes taken for the course [Machine learning](https://www.coursera.org/learn/machine-learning#syllabus) by Standford. Feel free to check the [assignments](https://github.com/3outeille/Coursera-Labs).
> Also, if you want to read my other notes, feel free to check them at my [blog](https://ferdinandmom.engineer/machine-learning/).

# I) Introduction

PCA is a **dimension reduction** algorithm. There are 2 motivations to use PCA:

1. Data compression.
2. Visualization.

### <ins>1) Data compression</ins>

- We may want to reduce the dimension of our features if we have a lot of redundant datas.
- To do this, we find highly correlated features, plot them, and make a new line that seems to describe both features accurately. We place all the new features on this single line.

Doing dimensionality reduction will reduce the total data we have to store in computer memory and will speed up our learning algorithm.

<ins>**Remark:**</ins> In dimensionality reduction, we are reducing our features rather than our number of examples.

### <ins>2) Visualization</ins>

It is not easy to visualize data that is more than three dimensions. We can reduce the dimensions of our data to 3 or less in order to plot it.

We need to find new features, $z_1$, $z_2$ (and perhaps $z_3$) that can effectively summarize all the other features.

<ins>**Example:**</ins> Hundreds of features related to a country's economic system may all be combined into one feature that you call "Economic Activity".

# II) Intuition

The goal of PCA is to find the best line that will **minimize the orthogonal distance between our points and the line** and **maximize the spread of the projected point on the line**, also called **variance**. (Here is a good [post](https://stats.stackexchange.com/questions/2691/making-sense-of-principal-component-analysis-eigenvectors-eigenvalues) to understand the intuition behind it)

As you can see in the gif, minimizing the orthogonal distance between our points and the line will also maximize the variance (respectively).

Red points are projections of the blue points onto the line.


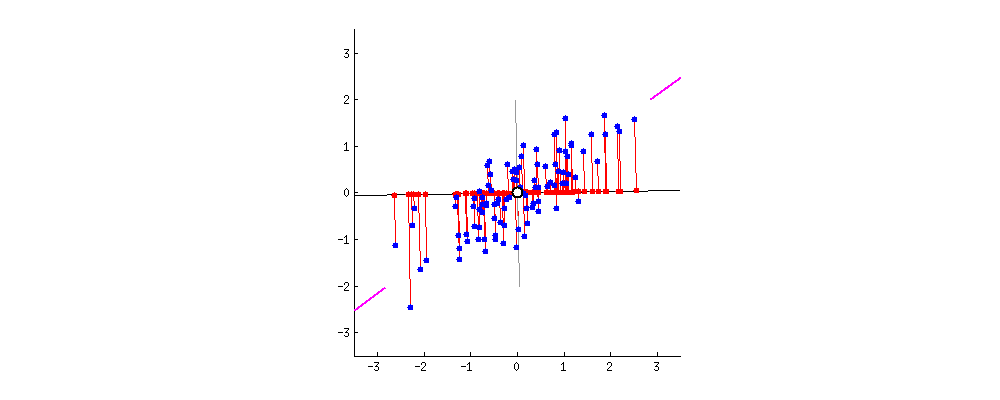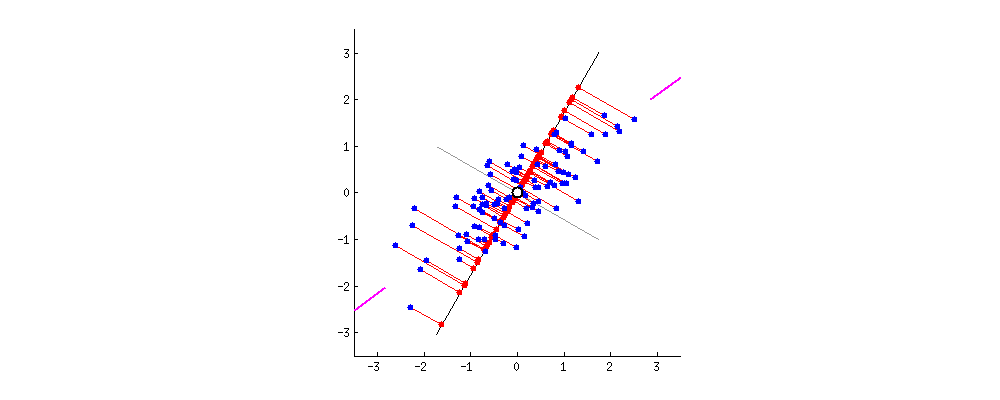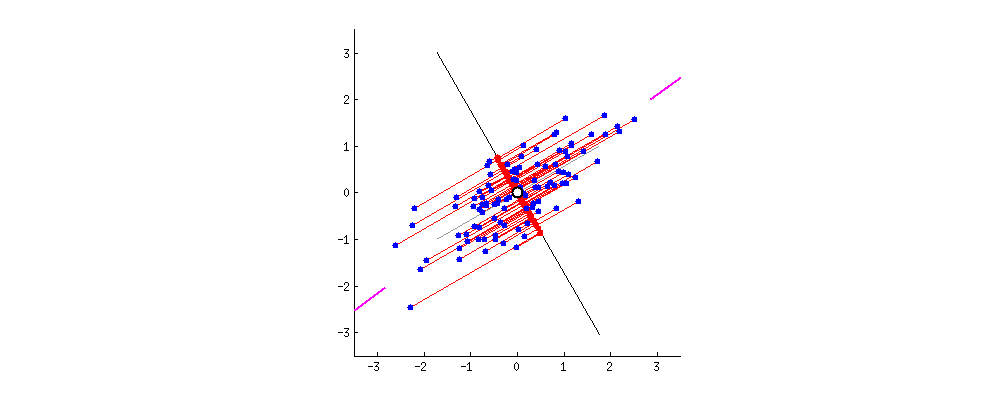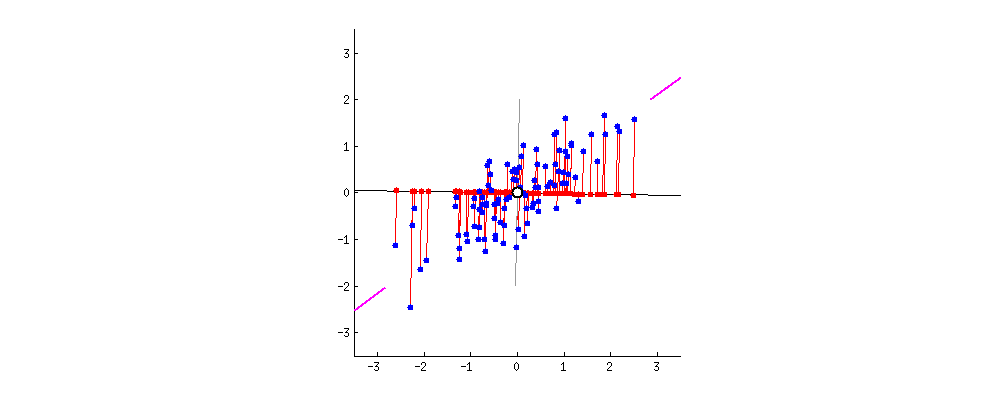
<ins>**Remark:**</ins>

PCA is not linear regression.

- In **linear regression**, we are minimizing the squared error from every point to our predictor line. These are vertical distances.
- In **PCA**, we are minimizing the shortest distance, or shortest orthogonal distances, to our data points.

More generally, in linear regression we are taking all our examples in $x$ and apply the parameters with $\theta$ to predict $y$.

In PCA, we are taking a number of features $x_1, x_2,..., x_n$ , and finding a closest common dataset among them. We aren't trying to predict any result and we aren't applying any theta weights to the features.

<ins>How do we minimize the orthogonal distance ?</ins>

We simply have to find a **direction** (a vector $z \in \mathbb{R}$ usually called **principal component**) onto which to project the data so as to minimize the projection error.

<div style="text-align:center">
<img src="https://raw.githubusercontent.com/valoxe/image-storage-1/master/blog-machine-learning/principal-component-analysis/3.png">
</div>
<br>

# III) Compressed representation

How do we find this direction ? By applying **PCA** algorithm:

1. **Feature scaling** on $x$.
2. We **compute** the **covariance matrix**.
3. We **compute** the **eigenvectors of the covariance matrix** (denoted as $U$). Eigenvectors of a covariance matrix are the **directions in which the data varies the most**.
4. Take **the first $k$ columns of the $U$ matrix** and **compute the new feature $z$**.

### <ins>1) Feature scaling on x</ins>

Apply **mean normalization** on features $x$.

1. Compute the mean, $\mu = \frac{1}{m}\sum_{i=1}^{m}x^{(i)}$
2. Compute the variance, $\sigma^2 = \frac{1}{m}\sum_{i=1}^{m}(x^{(i)})^2$
3. Compute mean normalization, $x_j^{(i)} = \frac{x_j^{(i)} - \mu_j}{\sigma^2}$

### <ins>2) Compute covariance matrix</ins>

$$\displaystyle\Sigma=\frac{1}{m}\sum_{i=1}^mx^{(i)}{x^{(i)}}^T\in\mathbb{R}^{n\times n}$$

### <ins>3) Compute eigenvector of covariant matrix U</ins>

One can use **singular value decomposition** (SVD) method.

### <ins>4) Compute the new feature z</ins>

Let's denoted $U_{reduce} = u_1,...,u_k \in \mathbb{R}^n$, the $k$ orthogonal principal eigenvectors of $\Sigma$. ($k$ is called the **number of principal components**)

We can now compute the new feature $z$, $z^{(i)} = U_{reduce}^T \cdot x^{(i)}$

# IV) Reconstruction from Compressed Representation

If we use PCA to compress our data, how can we uncompress our data, or go back to our original number of features?

We can do this with the equation: $x_{approx}^{(1)} = U_{reduce} \cdot z^{(1)}$.

**Note that we can only get approximations of our original data.**

# V) Choosing the Number of Principal Components

How do we choose $k$, also called **the number of principal components**? Recall that $k$ is the dimension we are reducing to.

One way to choose k is by using the **variance retention** formula:

$$\boxed{
\frac{\frac{1}{m} \sum_{i=1}^{m} (x^{(i)} - x_{approx}^{(i)})^2}{\frac{1}{m} \sum_{i=1}^{m} (x^{(i)})^2} \leq 0.01
}$$

with

- The average squared projection error: $\frac{1}{m} \sum_{i=1}^{m} (x^{(i)} - x_{approx}^{(i)})^2$
- The total variation in the data: $\frac{1}{m} \sum_{i=1}^{m} (x^{(i)})^2$

In other words, the squared projection error divided by the total variation should be less than one percent, so that **$99\%$ of the variance is retained**.

<ins>**Algorithm for choosing $k$:**<ins>

1. Try PCA with $k=1,2,…$
2. Compute $U_{reduce}, z, x$.
3. Check the formula given above that **$99\%$ of the variance is retained**. If not, go to step one and increase $k$.

This procedure would actually be horribly inefficient. We can use the matrix of **singular values** (obtained by using SVD) in the variance retained. Thus,

$$\boxed{
\frac{\sum_{i=1}^{k} S_{ii}}{\sum_{i=1}^{n} S_{ii}} \geq 0.99
}$$

# VI) Advice for applying PCA

The most common use of PCA is to speed up **supervised learning**.

Given a training set with a large number of features (e.g. $x^{(1)},…,x^{(m)} \in \mathbb{R}^{10000}$) we can use PCA to reduce the number of features in each example of the training set (e.g. $z^{(1)},…,z^{(m)} \in \mathbb{R}^{1000}$).

Note that we should define the PCA reduction from $x^{(i)}$ to $z^{(i)}$ only on the training set and not on the cross-validation or test sets. You can apply the mapping $z^{(i)}$ to your cross-validation and test sets after it is defined on the training set.

<ins>**Application of PCA**<ins>

- Compressions (choose $k$ by $\%$ of variance retain.)
- Reduce memory / disk needed to store data.
- Speed up algorithm.
- Visualization (choose $k=2$ or $k=3$)

Bad use of PCA is when it is used to try preventing overfitting. We might think that reducing the features with PCA would be an effective way to address overfitting. It might work, but is not recommended because it does not consider the values of our results y. Using just regularization will be at least as effective.

Don't assume you need to do PCA. Try your full machine learning algorithm without PCA first. Then use PCA if you find that you need it.