---
tags: TrRun5
id: Cont-B04_bundle-map.md
---
# 檜山トレラン5 B04 ファミリー/バンドル/マップ
$\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\Iff}{\Leftrightarrow }
\newcommand{\In}{\text{ in } }
\newcommand{\id}{\mathrm{id} }
\require{color}%
\newcommand{\Keyword}[1]{ \textcolor{green}{ \bf \text{#1} } }%
\newcommand{\For}{\Keyword{For }}%
\newcommand{\Let}{\Keyword{Let }}%
\newcommand{\WeWillDefine}{\Keyword{WeWillDefine }}%
\newcommand{\WeDefine}{\Keyword{WeDefine }}%
\newcommand{\Notation}{\Keyword{Notation }}%
%$
[B04-2 続 ファミリー/バンドル/マップ](https://hackmd.io/@m-hiyama/S1xMMiq85c) に続編あり。
## はじめに
(1) 形式的な概念定義、(2) 概念を名指す用語法、(3) 概念にまつわる気持ち/イメージ/習慣/典型例など、の三者を分離して、それぞれを確実に理解しよう、という話をした。分離して理解するトレーニングとして、本セミナーの主要テーマである「ファミリー/バンドル/マップ」を**自力で**解釈・分析してみよう。(ファミリー=コンテナ=多項式)
ファミリー/バンドル/マップ という3つの概念は==ほとんど差がなく==て、相互に変換可能である。ほぼ同じ概念に用語が山ほどあるのは、それだけ重要であることの証左でもある。
## 指標(形式的概念定義)
```desc
description basics
signature Map within Set {
0-mor A
0-mor B
1-mor f: A → B
}
```
↑集合圏を前提に写像概念を定義しても循環論法/同語反復のように思えるが、あとで参照するために Map という指標を定義しておく。
```desc
continue description basics
signature Bundle within Set {
0-mor E
0-mor B
1-mor p: E → B
}
```
↑指標を書いてみると、バンドルとマップの差はない、形式的・抽象的には==まったく同じ概念==である。にも関わらず用語法(後述)がガラッと変わるのはメンタルモデルが違うから。
```desc
continue description basics
signature Family {
0-mor I in Set
1-mor F: I → |Set| in SET
}
```
↑もうお馴染みファミリーの定義。コンテナとも多項式とも呼ぶ。
```desc
continue description basics
signature Schema {
0-mor K in Set
1-mor F: K → |Set| in SET
}
```
↑おまけにスキーマ。スキーマも形式的にはファミリーと==まったく同じ==。
## 用語定義
プレーンテキストで書けるように、次の記法を使う。
- InvImgOfPoint(-, -) : 点〈要素〉に対する写像の逆像集合 [3/ B12 「逆」のオーバーロード](https://hackmd.io/@m-hiyama/B1eADLqkY) 参照。
TeX記法との対応は:
$\For f:A \to B \In {\bf Set}\\
\For y \in B\\
\quad \text{InvImgOfPoint}(f, y) := f^{-1}(y) \;\in \mrm{Pow}(A)
%$
```term
terminology basics
vocabulary Bundle {
bundle :=> basics.Bundle // 概念としてのバンドル、冠詞なし
"a bundle" :=> a model of basics.Bundle
"the projection of a bundle" :=>
the p of (a model of basics.Bundle)
"the base {set | space} of a bundle" :=>
the B of (a model of basics.Bundle)
"a {fiber | fibre} of a bundle" :=> // ここの冠詞は a でよい
the InvImgOfPoint(p, x) for (
an element x of (
the B of (a model of basics.Bundle)
)
)
"the total {set | space} of a bundle" :=>
the E of (a model of basics.Bundle)
}
vocabulary Map {
map :=> basics.Map // 概念としてのマップ、冠詞なし
"a map" :=> a model of basics.Map
"the codomain of a map" :=>
the B of (a model of basics.Map)
"the domain of a map" :=>
the A of (a model of basics.Map)
}
vocabulary Family {
family :=> basics.Family // 概念としてのファミリー、冠詞なし
"a family" :=> a model of basics.Family
"the indexing set of a family" :=>
the I of (a model of basics.Family)
}
vocabulary Schema {
schema :=> basics.Schema // 概念としてのスキーマ、冠詞なし
"a schema" :=> a model of basics.Schema
"the set of keys of a schema" :=>
the K of (a model of basics.Schema)
"a key of a schema" :=>
an element of (
the K of (a model of basics.Schema)
)
}
```
次は日本語の呼び名、ウンザリしたら解釈・分析に頑張る必要はない。むしろ、==ドーデモイイという悟り==をひらいてもらいたい。(バンドルの全空間をバンドルと呼ぶ習慣は根強いので注意。)
```term
continue terminology basics
context バンドル for Bundle {
バンドル := bundle
バンドル := "a bundle"
{バンドルの}?射影 := "the projection of a bundle"
{バンドルの}?{ベース | 底}{集合 | 空間} := "the base {set | space} of a bundle"
{バンドルの}?フィイバー := "a {fiber | fibre} of a bundle"
{バンドルの}?全{集合 | 空間} := "the total {set | space} of a bundle"
バンドル := "the total {set | space} of a bundle" // この曖昧性に注意
束 = バンドル // これは翻訳語としての同義語
}
context マップ for Map {
{マップ | マッピング | 写像 | 関数} := map
{マップ | マッピング | 写像 | 関数} := "a map"
{マップの}?{余域 | 終域 | コドメイン} := "the codomain of a map"
{マップの}?{域 | 始域 | ドメイン} := "the domain of a map"
}
context ファミリー for Family {
ファミリー := family
ファミリー := "a family"
{インデックス{付き | 付けられた}}?集合{の}?族 := family
{インデックス{付き | 付けられた}}?集合{の}?族 := "a family"
{ファミリーの}?{インデックス | インデキシング}{集合 | セット}
:= "the indexing set of a family"
}
context スキーマ for Schema {
スキーマ := schema
スキーマ := "a schema"
型定義 = スキーマ // 同義語
{スキーマの}?{キー | フィールド名 | カラム名 | 属性名 | プロパティ名}の集合
:= "the set of keys of a schema"
{スキーマの}?{キー | フィールド名 | カラム名 | 属性名 | プロパティ名}
:= "a key of a schema"
}
```
## 相互変換
ファミリー/バンドル/マップ という3つの概念は相互に変換可能であることは、次の構成手続き〈construction procedure〉で分かる。
プレーンテキストで書けるように、次の記法を使う。
- Sigma(-, -) : ファミリーのシグマ構成(無限かも知れない足し算)
- Union(-, -) : ファミリーの無限かも知れない合併、コメント内でしか使ってないが
TeX記法との対応は:
$\For (I,\, F:I \to |{\bf Set}|) \in \text{ the 0-class of Family}\\
\quad \text{Sigma}(I, F) = \Sigma(F) := \sum_I F = \sum_{i\in I}F(i)\\
\quad \text{Union}(I, F) := \bigcup_{I}(F) = \bigcup_{i\in I}F(i)\\
%$
```desc
continue description basics
procedure bundleFromMap from a Map map
produces a Bundle bun
{
bun.E := map.A
bun.B := map.B
bun.p := map.f
}
procedure mapFromBundle from a Bundle bun
produces a Map map
{
map.A := bun.E
map.B := bun.B
map.f := bun.p
}
procedure familyFromMap from a Map map
produces a Family fam
{
fam.I := map.B
fam.F := λy∈map.B.( InvImgOfPoint(map.f, y) ∈|Set| )
}
procedure mapFromFamily from a Family fam
produces a Map map
{
map.A := Sigma(fam.I, fam.F)
map.B := fam.I
map.f := λ(i, y)∈Sigma(fam.I, fam.F).( i ∈fam.I )
// Sigma(fam.I, fam.F) ⊆ fam.I × Union(fam.I, fam.F)
}
```
これで、バンドル←→マップ、マップ←→ファミリー が1:1対応するのが分かった、当然に バンドル ←→ ファミリー も1:1対応し、三者は相互変換可能。
<b>[追記]</b>「1:1対応」という言い方は不正確。[B04-2 続 ファミリー/バンドル/マップ](https://hackmd.io/@m-hiyama/S1xMMiq85c) を見よ。<b>[/追記]</b>
様々な用語やメンタルモデルの奥には、単純な3つの概念があり、それら3つの概念も事実上同じであり、つまりは単純なひとつの概念を扱っているだけ、ということを強く意識する。そうすれば、「要するに単純なひとつの概念」という悟りがひらけ、大幅な時間節約になる。
==構文的注意:== 構成手続きを簡潔に書きたいなら次のようでもよい。簡潔がいいかどうかはちょっと判断に苦しむ。
```desc
procedure mapFromFamily from a Family
produces a Map
{
A := Sigma(I, F)
B := I
f := λ(i, y)∈Sigma(I, F).( i ∈I )
}
```
==語学的注意:== 記号の読み方。手続き内の := は、is-defined-by と読むとよい。bun.E := map.A は次のように読める。
```
the E of (a model bun of Bundle)
is-defined-by
the A of (a model map of Map)
(指標 Bundle の任意のモデル bun) の E
は、
(指標 Map の任意のモデル map) の A
により定義される。
```
<b>[追記]</b>ここの「任意の」の用法はちょっとおかしい。[B04-2 続 ファミリー/バンドル/マップ](https://hackmd.io/@m-hiyama/S1xMMiq85c) を見よ。<b>[/追記]</b>
==メンタル的注意:== ほとんど同じ3つの概念を、メンタルに〈気持ちとして、感覚として、実感として〉納得するには、絵を描くのが有効。各自で絵を描くべきではあるが、参考例を挙げる。左からマップのイメージ(要素→要素 対応)、バンドルのイメージ(ファイバーを考える)、ファミリーのイメージ(向きが逆)。
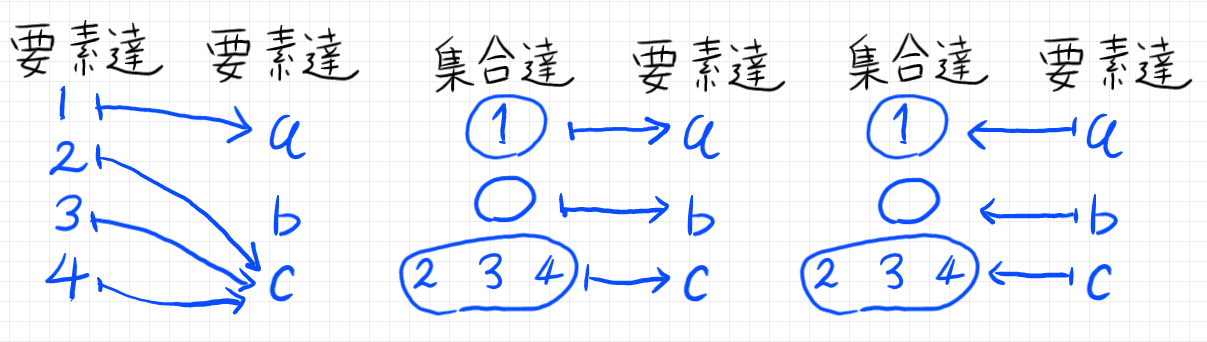
正確に言えば、バンドルのファイバーはタギングされている(依存ペアだ)し、ファミリーの値である集合達は重なる可能性がある。あくまで最初のイメージを作るための絵。
[B04-2 続 ファミリー/バンドル/マップ](https://hackmd.io/@m-hiyama/S1xMMiq85c) に続編あり。