本章我们学习一种常见的监督式机器学习算法,决策树。
# 决策树算法简介
决策树是一种树形结构,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果。在分类问题中,表示基于特征对实例进行分类的过程。学习时,利用训练数据,根据损失函数最小化的原则建立决策树模型;预测时,对新的数据,利用决策模型进行分类。
# 决策树模型
### 基本概念
学习过树形结构的同学应该能够比较好的理解决策树中的一些概念,可以跳过这一小节。
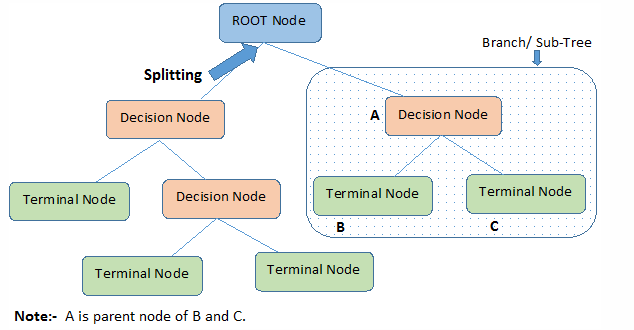
决策树所涉及到的概念包括:
1. 根结点:它表示整个样本集合,并且该节点可以进一步划分成两个或多个子集。
2. 拆分:表示将一个结点拆分成多个子集的过程。
3. 决策结点:当一个子结点进一步被拆分成多个子节点时,这个子节点就叫做决策结点。可以理解为做出选择
4. 叶子结点:无法再拆分的结点被称为叶子结点。在树结构中为底层节点
5. 剪枝:移除决策树中子结点的过程就叫做剪枝,跟拆分过程相反,常用于优化。
6. 分支/子树:一棵决策树的一部分就叫做分支或子树。
7. 父结点和子结点:一个结点被拆分成多个子节点,这个结点就叫做父节点;其拆分后的子结点也叫做子结点。(根节点也是父亲节点)
### 模型建立
#### 特征选择
把不同的特征作为决策的标准生成的决策树模型是不同的。一般而言,决策树的建立有三种方法:ID3, C4.5以及CART。其中,CART的分类效果一般优于其他两个方法。在本章中,我们会详细介绍这三种方法。
#### 决策树的生成
决策树通过选择的特征来评估标准,递归地进行生成子节点的过程,直到数据集不再可分。每一次数据集的划分,都希望各个子集的不确定性更小
#### 剪枝
对于过拟合的决策树模型,需要进行适当的剪枝,缩小树结构的规模。
### 模型优缺点
决策树的优点:
1. 具有可读性,如果给定一个模型,根据所产生的决策树很容易推理出相应的逻辑表达。
2. 分类速度快,能在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
决策树的缺点:
1. 对**未知**的测试数据未必有好的分类能力,即可能发生过拟合现象,此时可采用剪枝或随机森林。(随机森林我们会在之后的文章中提到)
# ID3算法
由信息增益的原理来进行决策对于一组数据,熵越小,代表分类实现效果越好。
### 信息增益
熵是随机变量不确定性的度量,也就是熵越大,则随机变量的不确定性越大,熵越小,则随机变量的不确定性越小。其数学定义如下:
假设X是取得有限个值的离散随机变量,那么它的概率分布为
$$
p\left(X=x_{i}\right)=p_{i}
$$
它的熵为
$$
H(x)=-\sum_{i=1}^{n} p_{i} \log p_{i}
$$
条件熵H(Y|X)表示在已知随机变量X的条件下,随机变量Y的**不确定性**。随机变量X给定的条件下随机变量Y的条件熵H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望:
$$
H(Y \mid X)=\sum_{i=1}^{n} p_{i} H\left(Y \mid X=x_{i}\right)
$$
信息增益表示由于得知特征A的信息后的数据集D的分类不确定性减少的程度,定义为:
$$
\mathrm{H}(\mathrm{D})-\mathrm{H}(\mathrm{D} \mid \mathrm{A})
$$
# C4.5算法
### 算法简介
通过对ID3的学习,可以知道ID3存在一个问题,那就是越细小的分割分类错误率越小,所以ID3会越分越细。C4.5算法与ID3相似,但做了一些改进,即通过信息增益比来作为选择特征的标准。
### 信息增益比
特征A对训练数据集D的信息增益比GainRatio(D,A)定义为其信息增益Gain(D,A)与训练数据集D的经验熵H(D)之比,即
$$
\operatorname{GainRatio}(D, A)=\frac{\operatorname{Gain}(D, A)}{H(D)}
$$
# CART算法
### 算法简介
CART也被成为回归分类树,它是一个二叉树。所以CART只能将一个父节点分成两个子节点,这里通过Gini指数来决定如何分裂。
### Gini指数
总体内包含的类别越杂乱,Gini指数越大。在分类问题中,假设有k个类,样本点属于第k类的概率为Pk,则概率分布的Gini指数定义为:
$$
\operatorname{Gini}(p)=\sum_{i=1}^{K} p_{i}\left(1-p_{i}\right)
$$
由于 $\sum_{i=1}^{K} p_{i}=1$ 我们可以得到简化公式:
$$
\operatorname{Gini}(p)=1-\sum_{i=1}^{K} p_{i}^{2}
$$
样本集合D中的基尼系数:
$$
\operatorname{Gini}(D)=1-\sum_{i=1}^{K}\left(\frac{\left|C_{i}\right|}{|D|}\right)^{2}
$$
值得一提的是,CART是一个二叉树,当时用某个特征划分集合样本时只有两个集合:
1.等于给定的特征值的样本集合D1
2.不等于给定的特征值的样本集合D2
所以样本集合D可以划分为两个子集:
$$
\operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right)
$$
# 代码实现
接下来我们将介绍基于sklearn的决策树代码实现。
```python
# 数据导入与切分
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
iris = load_iris()
X = iris.data
Y = iris.target
```
针对不同算法的决策树构建,我们需要调整DecisionTreeClassifier中的参数。以criterion为例,entropy代表通过信息熵对节点做分化,gini代表通过Gini指数对节点做分化。
```python
DST = DecisionTreeClassifier(criterion='entropy')# 信息熵
x_train,x_test,y_train,y_test = train_test_split(X,Y,test_size=0.3,random_state=0)
DST.fit(x_train,y_train)
from sklearn import metrics
pred = DST.predict(x_test)
accuracy = metrics.accuracy_score(y_test,pred)
print("The accuracy is %.3f"% accuracy)
```
# 作业
使用sklearn提供的决策树模型对手写数字数据集的数据进行预测。手写数字数据集使用方法如下:
```python
from sklearn.datasets import load_digits
digits = load_digits()
```
# 参考来源
1. [https://shuwoom.com/?p=1452](https://shuwoom.com/?p=1452)
2. 《机器学习实战》Peter Harringto[ml](https://www.cnblogs.com/muzixi/p/6566803.html)
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet