# #2 Class Photos

###### tags:`Greedy Algorithm` `Easy`

## Issue

It's photo day at the local school, and you're the photographer assigned to take class photos. The class that you'll be photographing has an even number of students, and all these students are wearing red or blue shirts. In fact, exactly half of the class is wearing red shirts, and the other half is wearing blue shirts. You're responsible for arranging the students in two rows before taking the photo. Each row should contain the same number of the students and should adhere to the following guidelines:
All students wearing red shirts must be in the same row.
All students wearing blue shirts must be in the same row.
Each student in the back row must be strictly taller than the student directly in front of them in the front row.
You're given two input arrays: one containing the heights of all the students with red shirts and another one containing the heights of all the students with blue shirts. These arrays will always have the same length, and each height will be a positive integer. Write a function that returns whether or not a class photo that follows the stated guidelines can be taken.

Note: you can assume that each class has at least 2 students.

### Sample Input

redShirtHeights = [5, 8, 1, 3, 4]
blueShirtHeights = [6, 9, 2, 4, 5]

### Sample Output

true // Place all students with blue shirts in the back row.

### Hints
:::spoiler Hint 1
Start by determining which row will have the students wearing blue shirts and which row will have the students wearing red shirts. Once you know this, how can you determine if it's possible to take the photo?
:::

:::spoiler Hint 2
The shirt color of the tallest student will determine which students need to be placed in the back row. The tallest student can't be placed in the front row because there's no student taller than them who can be placed behind them.
:::

:::spoiler Hint 3
Once you know which students should be placed in each row, you can simply check if each student in the back row can be paired with a student in the front row who is shorter than them. If you can't find a satisfactory pairing for every student in the back row, then you can't take the photo.
:::

:::spoiler Hint 4
Sort each input array in descending order, then determine which students will be in the front and back rows following Hint #2. After this, simply loop through your sorted input arrays, and check if the current tallest student in the back row is taller than the current tallest student in the front row. If you find that the current tallest student (one that has yet to be placed) in the back row isn't taller than the current tallest student in the front row, then the photo can't be taken.
:::

### Optimal Space & Time Complexity

:::spoiler Answer
O(nlog(n)) time | O(1) space - where n is the number of students
:::

<br>

## Solutions

### Official

:::spoiler Solution 1

// O(nlog(n)) time | O(1) space - where n is the number of students
function classPhotos(redShirtHeights, blueShirtHeights) {
  redShirtHeights.sort((a, b) => b - a);
  blueShirtHeights.sort((a, b) => b - a);
  const shirtColorInFirstRow = redShirtHeights[0] < blueShirtHeights[0] ? 'RED' : 'BLUE';
  for (let idx = 0; idx < redShirtHeights.length; idx++) {
    const redShirtHeight = redShirtHeights[idx];
    const blueShirtHeight = blueShirtHeights[idx];
    if (shirtColorInFirstRow === 'RED') {
      if (redShirtHeight >= blueShirtHeight) return false;
    } else if (blueShirtHeight >= redShirtHeight) return false;
  }
  return true;
}

:::

### Everyone's

:::spoiler 東

// Time O(nlogn), Space O(1) | n is the numbers of students
function classPhotos(redShirtHeights, blueShirtHeights) {
  redShirtHeights.sort((a,b) => a - b);
  blueShirtHeights.sort((a,b) => a - b);
  
  if (redShirtHeights[0] === blueShirtHeights[0]) return false;
  
  const backRowColor = redShirtHeights[0] > blueShirtHeights[0] ? "red" : "blue";
  for(let i = 0; i < redShirtHeights.length; i++){
    if(backRowColor === "red" && redShirtHeights[i] <= blueShirtHeights[i]) return false;
    if(backRowColor === "blue" && redShirtHeights[i] >= blueShirtHeights[i]) return false;
  }
  return true;
}

:::

<br>

:::spoiler Hao

/**
 * Time complexity: O(N) where N stands for the number of students;
 * Space complexity: O(1);
 */

 function classPhotos(redShirtHeights, blueShirtHeights) {
  redShirtHeights.sort((a, b) => a - b);
  blueShirtHeights.sort((a, b) => a - b);

  const isFirstRedBackRow = redShirtHeights[0] > blueShirtHeights[0];
  const isPhotoFollowGuide = redShirtHeights.reduce((res, redHeight, redIdx) => {
    if (!res) return res;

    const blueHeight = blueShirtHeights[redIdx];
    return (redHeight !== blueHeight) && isFirstRedBackRow === (redHeight > blueHeight);
  }, true);

  return isPhotoFollowGuide;
}

:::

<br>

:::spoiler YC

//time: O(nlogn), space: O(1) - where n is the length of the given arrays
function classPhotos(redShirtHeights, blueShirtHeights) {
  redShirtHeights.sort((a,b) => a-b);
  blueShirtHeights.sort((a,b) => a-b);
  let backRow;
  let frontRow;
  if(redShirtHeights[0] - blueShirtHeights[0] > 0){
    backRow = redShirtHeights;
    frontRow = blueShirtHeights;
  }
  else{
    backRow = blueShirtHeights;
    frontRow = redShirtHeights;
  }
  
  for(let i = 0; i < backRow.length; i++){
    if (backRow[i] - frontRow[i] <= 0) return false
  }
  
  return true;
}

:::

<br>

:::spoiler 月薪

/*
  Time: O(n), where n is the length of redShirtHeights
  Space: O(1) 
*/ 
function classPhotos(redShirtHeights, blueShirtHeights) {
  redShirtHeights.sort((a,b) => b - a);
  blueShirtHeights.sort((a,b) => b - a);
  const { length } = redShirtHeights;
  let frontRed = true;
  let frontBlue = true;
  for(let i = 0; i < length; i++){
    if(redShirtHeights[i] >= blueShirtHeights[i]){
      frontRed = false;
    }
    if(blueShirtHeights[i] >= redShirtHeights[i]){
      frontBlue = false;
    }
  }
  return frontRed || frontBlue
}

:::

<br>

:::spoiler Becky

:::

<br>

## Supplement
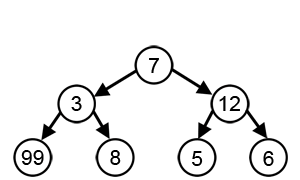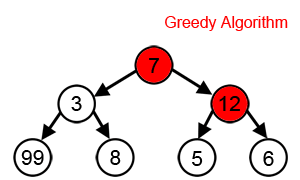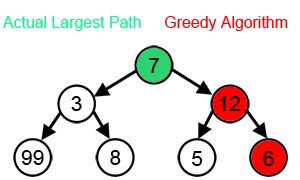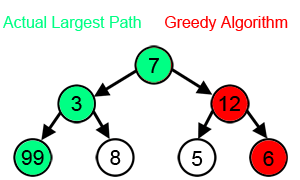
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage.

In many problems, a greedy strategy does not produce an optimal solution.