# pbr
## brdf
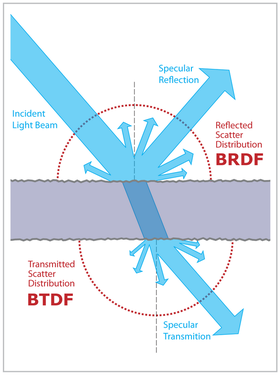
In computer graphics have investigated the material interactions with the light and Summarized the equation which is called brdf(bidirectional reflectance distribution function).
## Phong model
$V:\text{surface to the view direction}$
$N:\text{surface normal direction}$
$L:\text{surface to the light direction}$
$R:\text{the direction of light reflect to surface normal}$
$H:\text{surface to the light direction}$
The classic model of the brdf is Phong
the Phong shading separates the lighting into 3 parts which are ambient, diffuse, specular. Model content 2 things the color and shininess which control the diffuse color and highlight of the model.

$$\underset{Phong}{brdf(n,l,v,r,h)}= \underset{ambient}{k_aA}+\sum_{each \ light}\{\underset{diffuse}{k_dD(n,l)}+\underset{specular}{k_sS(v,h)}\}$$

$k_a,k_d,k_s:\text{is intensity of ambient(環境光) , diffuse(漫射) , specular(高光)}$
$A=\text{ambientColor}$
$D(n,l)=modelColor\times lightColor\times dot(l,n)$
$S(n,h)=lightColor\times pow(dot(h,n),modelShininess)$

## physically based rendering model

### The microfacet model
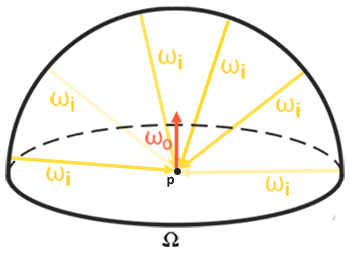
the real lighting we see is baisc base on countless ray. By integration all the light from the possible direction(semi-sphere) we can get the color equation of whole surface.
$$color= \int_\omega f_{brdf}(w_0,w_i)\ dw_i$$
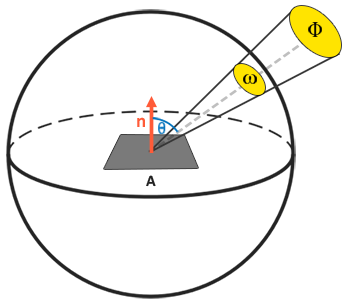
when the light angle and normal angle is geting more orthogonal the same among of engey is need to divide to more area so the intensity less.

$w_0=V(\text{direction of light})$
$\triangle w=dot(w_i,w_0)$
$$color= \int_\omega f_{brdf}(w_0,w_i)I_{}(w_0,w_i)\ dw_i$$

### equation
$\alpha=\text{roughness of the model}$
$\underset{PBR}{brdf(n,l,v,r,h)}=\underset{each \ light}{\sum}(\{ \int_\omega k_dD(w_0,w_i) +k_s S(w_0,w_i))L_{}(w_0,w_i) \ dw_i\}$
$\underset{PBR}{brdf(n,l,v,r,h)}=\underset{each \ light}{\sum}(\{ \int_\omega k_d \frac{modelColor}{\pi} +k_s \frac{NDF(n,h, \alpha )F(h,v)G(n,v,h,l,\alpha)}{4 (w_0 \cdot n)(w_i \cdot n)})L_{}(w_0,w_i)\ dw_i\}$

### lambert

$D(w_0,w_i)=f_{lambert}$
### Normal Distribution Function
$NDF\text{(Normal Distribution Function)}:$When the surface is getting rough the highlight begind to diffuse on surface.

### fresnel
$F\text{(Fresnel)}:$Describes the ratio of light that gets reflected over the light that gets refracted.