# 深層学習day1
## 1. 入力層~中間層
### 要点
ニューラルネット全般の話
- 回帰、分類両方に使える
- 回帰
- 連続的な値
- ランキング(順位予想など)
- 分類
- 離散的な結果
- 4つ以上の中間層=深層学習、ディープニューラルネットワーク
- 例
- 自動売買
- チャットボット
- 翻訳
- 音声解釈
- 囲碁、将棋AI
得た出力結果と正解データとの差を表した関数、誤差関数
結果をニューラル層にフィードバックして重みとバイアスの更新
誤差関数
$E_{n}(\boldsymbol w)$
→
$\displaystyle \nabla E_{n}(\boldsymbol w)=\frac{\partial E}{\partial \boldsymbol w}$
→ 重み更新
$\boldsymbol w^{t+1}=\boldsymbol w^{t}-\epsilon d\nabla E_{n}(\boldsymbol w)$
### 実装演習結果サマリー、考察
**1_1_forward_propagation.ipynb**
順伝播(3層・複数ユニット)
```
*** 入力 ***
[1. 2.]
##### ネットワークの初期化 #####
*** 重み1 ***
[[0.1 0.3 0.5]
[0.2 0.4 0.6]]
*** 重み2 ***
[[0.1 0.4]
[0.2 0.5]
[0.3 0.6]]
*** 重み3 ***
[[0.1 0.3]
[0.2 0.4]]
*** バイアス1 ***
[0.1 0.2 0.3]
*** バイアス2 ***
[0.1 0.2]
*** バイアス3 ***
[1 2]
##### 順伝播開始 #####
*** 総入力1 ***
[0.6 1.3 2. ]
*** 中間層出力1 ***
[0.6 1.3 2. ]
*** 総入力2 ***
[1.02 2.29]
*** 出力1 ***
[0.6 1.3 2. ]
出力合計: 3.9
```
ノードの入力である「重みx入力xバイアス」の所は線形の関係であるが、
このあとの活性化関数を通して非線形の関係で表現できる(線形だけで表現できなかった事ができる)
### 確認テスト
---

---

**この数式をPythonで書け**
**$u=w_{1}x_{1}+w_{2}x_{2},,w_{4}x_{4}+b$**
**$=Wx+b$**
答え
```python=
W=np.array([w1,w2,w3,w4])
X=np.array([x1,x2,x3,x4])
u=np.dot(W, x)+b
```
**1-1のファイルから中間層の出力を定義しているソースを抜き出せ**
```python=
# 1層の総入力
u1 = np.dot(x, W1) + b1
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総入力
u2 = np.dot(z1, W2) + b2
# 2層の総出力
z2 = functions.relu(u2) <---------ここ
# 出力層の総入力
u3 = np.dot(z2, W3) + b3
# 出力層の総出力
y = u3
```
プログラミングでルールを作り、当てはめるのではなく、
学習されたニューラルネットを用いて、入力値から出力を求める事
最適化を行うパラメータ
→重みとバイアス
---
### その他関連事項
ニューラルネットの入力は次元間で関連があるデータが好ましい(画像のピクセル、時系列データ)との事だが
自分が確認テストで出した、True or False、カテゴリカル、足の本数といった
尺度がことなるものを混ぜるのはあまりよろしくないかもしれない。
それともその辺もよしなに処理してくるのか。
G検定でも出てきたが改めて尺度について調べた。
- 名義尺度 区別、分類するため。名前、電話番号など
- 順序尺度 大小はあるが、間隔に意味はない。足し算、引き算に意味がない。 競争の順位、検定1級/準1級/2級など
- 間隔尺度 大小、間隔に意味があるもの。除算、乗算に意味はない。気温、テストの点数
- 比例尺度 0の値(原点)に意味があるもの。質量、長さ。
## 2. 活性化関数
### 要点
**中間層の活性化関数**
- ReLU関数
もっとも使われている関数
```python=
def relu(x):
return
np.maximum(0, x)
```
$f(x) = \left\{
\begin{array}{ll}
x & (x > 0) \\
0 & (x \leq 0)
\end{array}
\right.$
勾配消失問題の回避とスパース化に貢献
- シグモイド関数
$\displaystyle f(u)=\frac{1}{1+e^{-u}}$
1 or 0ではなく、中間が表現できる。
ただ入力が大きい所で変化が微小になる。→**勾配消失問題**
- ステップ関数:もうあまり使われていない
$f(x) = \left\{
\begin{array}{ll}
1 & (x \geq 0) \\
0 & (x \lt 0)
\end{array}
\right.$
**出力層用の活性化関数**
- ソフトマックス関数
- 恒等写像(そのまま出力)
- シグモイド関数(ロジスティック関数)
### 実装演習結果サマリー、考察
**1_1_forward_propagation.ipynb**
特になし。前章と同じ。
**1_2_back_propagation.ipynb**
```
##### ネットワークの初期化 #####
*** 重み1 ***
[[0.1 0.3 0.5]
[0.2 0.4 0.6]]
*** 重み2 ***
[[0.1 0.4]
[0.2 0.5]
[0.3 0.6]]
*** バイアス1 ***
[0.1 0.2 0.3]
*** バイアス2 ***
[0.1 0.2]
##### 順伝播開始 #####
*** 総入力1 ***
[[1.2 2.5 3.8]]
*** 中間層出力1 ***
[[1.2 2.5 3.8]]
*** 総入力2 ***
[[1.86 4.21]]
*** 出力1 ***
[[0.08706577 0.91293423]]
出力合計: 1.0
##### 誤差逆伝播開始 #####
*** 偏微分_dE/du2 ***
[[ 0.08706577 -0.08706577]]
*** 偏微分_dE/du2 ***
[[-0.02611973 -0.02611973 -0.02611973]]
*** 偏微分_重み1 ***
[[-0.02611973 -0.02611973 -0.02611973]
[-0.13059866 -0.13059866 -0.13059866]]
*** 偏微分_重み2 ***
[[ 0.10447893 -0.10447893]
[ 0.21766443 -0.21766443]
[ 0.33084994 -0.33084994]]
*** 偏微分_バイアス1 ***
[-0.02611973 -0.02611973 -0.02611973]
*** 偏微分_バイアス2 ***
[ 0.08706577 -0.08706577]
##### 結果表示 #####
##### 更新後パラメータ #####
*** 重み1 ***
[[0.1002612 0.3002612 0.5002612 ]
[0.20130599 0.40130599 0.60130599]]
*** 重み2 ***
[[0.09895521 0.40104479]
[0.19782336 0.50217664]
[0.2966915 0.6033085 ]]
*** バイアス1 ***
[0.1002612 0.2002612 0.3002612]
*** バイアス2 ***
[0.09912934 0.20087066]
```
### 確認テスト
---
**線形と非線形の違いを図に書いて、簡易に説明せよ**

答えより少し上の説明では(あって無くもなさそうだが)足りない。
> 線形な関数は
> 加法性:$f(x+y)=f(x)+f(y)$
斉次性:$f(kx)=kf(x)$
を満たす。
> 非線形な関数は加法性、斉次性を満たさない
例えば$y=x^{2}$の場合、$(1)^{2}+(2)^{2}\neq(1+2)^{2}$
これは非線形。
---
**配布されたソースコードより$z=f(u)$該当する箇所を抜き出せ**
1_1_forward_propagation_after.ipynb
```python
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総出力
z2 = functions.relu(u2)
```
---
### その他関連事項
入力層の設計
- 入力層として取るべきでないデータ
- 欠損値が多いデータ
- 誤差の大きいデータ
- 出力そのもの、出力を加工した情報
- 連続性のないデータ
- 無意味な数が割り当てられているデータ
- 欠損値の扱い
- ゼロで埋める
- 入力値(特徴量)として採用しない
- 欠損値を含む集合を除外
- 数値の正規化(1-0に収める)、正則化(平均ゼロ、分散1)
- データの結合
## 3. 出力層
### 要点
出力層の役割
人の欲しい形に合わせる。
分類であれば、各クラスの確率。
**損失関数**
予測と答えの差を関数で表す
ニューラルネットでは一般的に二乗和誤差が使われる
$\displaystyle E=\frac{1}{2}\sum_{k}(y_{k}-t_{k})^{2}$
$y_{k}$:ニューラルネットの出力
$t_{k}$:教師データ
$k$: データの次元数
- 分類問題の場合、誤差関数にクロスエントロピー誤差を用いる
**交差(クロス)エントロピー**
$\displaystyle E=-\sum_{k}t_{k}\log y_{k}$
$y_{k}$:ニューラルネットの出力
$t_{k}$:教師データ
(one-hot表現=[1,0,0,0] 正解が1。実質正解のところだけ計算される)
$k$: データの次元数
正解箇所の出力値が小さい→$\log y_{k}$は負に大きくなる→Eが大きくなる
出力値がMaxで1の時→$\log y_{k}$は0に近い→Eも0に近くなる
**出力層の活性化関数**
出力層と中間層の違い
[値の強弱]
- 中間層:しきい値の前後で信号の強弱を調整
- 出力層:信号の大きさ(比率)はそのままに変換
[確率出力]
- 分類問題の場合、出力層の出力は0-1の範囲に限定し、
総和を1とする必要がある↓
- **ソフトマックス関数**
複数値からなるベクトルを入力し、正規化
$\displaystyle y_{k}=\frac{exp(a_{k})}{\sum_{i=1}^{K}exp(a_{i})}$
$n$:出力層の数
$y_{k}, a_{k}$: k番目の出力信号、入力信号
大文字$K$は全部のクラス数。他の式でもよく$K$で出てくる。
- 恒等写像(回帰問題)
入力をそのまま使う
$f(u)=u$
- シグモイド関数
$\displaystyle S(x)=\frac{1}{1+exp(-x)}$
| | 回帰 | 二値分類 | 多クラス分類 |
|-------|-------- | -------- | -------- |
|活性化関数|恒等写像 | シグモイド関数 | ソフトマックス関数 |
|誤差関数|二乗誤差| 交差エントロピー | 交差エントロピー |
### 実装演習結果サマリー、考察
なし
### 確認テスト
**なぜ引き算でなく二乗するか答えよ**
誤差がマイナスになった場合に値が相殺されてしまう事を防ぐため
(教材答え)
> 引き算するとトータルでゼロになってしまう
**二乗和誤差の1/2はどういう意味を持つか**
あとあとで微分する際に式の二乗の部分が降りてきて1になり便利
(教材答え)
> 誤差逆伝播の計算で誤差関数の微分を用いるがその際の計算式を
簡単にするため。本質的な意味はない
感想:
最近色々な数式を見ていると「便利だからこれを付けます」
のように意外と自由な印象を受ける。
**ソフトマックス関数①~③の数式に該当するソースコードを示し、1行づつ処理の説明をせよ**
function.softmax()より
```python=
# 出力層の活性化関数
# ソフトマックス関数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0) # 2, 3
return y.T # 1
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
```
最終行で①~③の処理を含んでいる
**交差エントロピー式①、②の数式に該当するソースコードを示し、1行づつ処理の説明をせよ**
function.softmax()より
```python=
# クロスエントロピー
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
```
最終行が対応するところ
### その他関連事項
- たまに出てくるargmax
- maxが最大値を返すとすると、argmaxは出力最大値を取る入力の集合を返す。argminも同様
(参考文献 P51より)
- なぜ活性化関数が非線形関数でないと駄目か?
- $y=ax$だといくら計算していっても単純に別の線分に直しただけ。多層にする意味がない。
```
参考文献
ゼロから作るDeepLearning
```
## 4. 勾配降下法
### 要約
学習を通して最も誤差が小さくなるネットワークにしたい。
→$E(w)$で表せる誤差が最小となるようなパラメータ$w$を見つける事
- 3つの学習させる方法
- 勾配降下法
$\displaystyle w^{(t+1)}=w^{(t)}-\epsilon\nabla E$
$\displaystyle \nabla E=\frac{\partial E}{\partial \boldsymbol w}=[\frac{\partial E}{\partial w_{1}},,,\frac{\partial E}{\partial w_{M}}]$
- 確率的勾配降下法
- ミニバッチ勾配降下法
- 学習率
大きすぎる→とびこして最小の所にたどりつかない
小さすぎる→なかなか辿り着かない。局所解に陥りやすい。
- 局所解
ある範囲においての局所解
- 学習をうまくやるための手法
- Momentum
- AdaGrad
- Adadelta
- **Adam**
#### 確率的勾配降下法(SGD)
ランダムに抽出したサンプルの誤差
$w^{(t+1)}=w^{(t)}-\epsilon \nabla E_{n}$
抽出したサンプルに対しての誤差。
- メリット
- データが冗長な場合の計算コストの軽減
- 望まない局所極小解に収束するリスクの軽減
- オンライン学習ができる
#### ミニバッチ勾配降下法
ランダムに分割したデータの集合(ミニバッチ)$D_{t}$に属するサンプルの平均誤差
確率的勾配降下法(再掲)
$w^{(t+1)}=w^
{(t)}-\epsilon \nabla E_{n}$
ミニバッチ勾配降下法
$w^{(t+1)}=w^
{(t)}-\epsilon \nabla E_{t}$
$\displaystyle E_{t}=\frac{1}{N_{t}}\sum_{n \in D_{t}}E_{n}$
$N_{t}=|D_{t}|$
### 実装演習結果サマリー、考察
**1_3_stochastic_gradient_descent.ipynb**
確率的勾配降下法

学習率を下げると収束まで時間がかかる(0.06->0.02)

- 分類問題の場合、誤差関数にクロスエントロピー誤差を用いる
### 確認テスト
**1_3_stochastic_gradient_descent.ipynb**
**オンライン学習とは何か2行でまとめよ**
学習で重みの計算に一度に学習データを全部使わず、
一部のデータを使用して重みの計算を行っていく
(すこし違う)
授業答え
学習データが入ってくるたびに都度パラメータを更新し、学習を進めていく方法。
一方、バッチ学習では一度にすべての学習データを使ってパラメータ更新を行う
(バッチの場合、一度にメモリに全てデータを乗せる必要がある。)
**この数式$w^{(t+1)}=w^{(t)}-\epsilon \nabla E_{t}$の意味を図に書いて説明せよ**

答え
エポックがt。1エポックは全てデータ(全てのミニバッチ)での学習が1回終わったところ。
そして1回$w$を更新。次にt+1となる。これを何回も繰り返す。
### その他関連事項
**バッチ、ミニバッチ、オンラインについて補足**
バッチ学習
全ての学習用データを使い、同じ目的関数の最適化を行う。
→学習順番にあまりよらない、局所解に陥りやすい、メモリを使う。
学習結果は安定しやすい。学習の収束が早い
ミニバッチ学習
エポックごとにデータを変える→毎回最適化すべて損失関数が異なる
→局所解に陥りにくい(事が期待される)
オンライン学習
一つのデータを取り出して重みの更新
→直近の外れ値に反応しやすい
参考文献:ディープラーニングE資格問題集(P163)
## 5. 誤差逆伝播法
### 要約
$\displaystyle \nabla E=\frac{\partial E}{\partial\boldsymbol w}=[\frac{\partial E}{\partial w_{1}}・・・\frac{\partial E}{\partial w_{M}}]$
の計算をどうするか。
算出された誤差を出力層側から順に微分し、前の層へと伝播させる。
最小限の軽s何で各パラメータでの微分値を解析的に計算する手法
**微分の連鎖率を使う**
合成関数$f(g(x))$で$t=g(x)$と置くと
$\displaystyle \frac{\partial f}{\partial x}=\frac{\partial f}{\partial t}\frac{\partial t}{\partial x}$
ので一つのパーセプトロンで出力$y$とすると
$\displaystyle \frac{\partial E}{\partial w_{i}}=\frac{\partial E}{\partial y}\frac{\partial y}{\partial w_{i}}$
### 実装演習結果サマリー、考察
**1_4_1_mnist_sample.ipynb**
デフォルト設定
```
Generation: 970. 正答率(トレーニング) = 0.88
: 970. 正答率(テスト) = 0.9204
Generation: 980. 正答率(トレーニング) = 0.92
: 980. 正答率(テスト) = 0.9195
Generation: 990. 正答率(トレーニング) = 0.94
: 990. 正答率(テスト) = 0.9217
Generation: 1000. 正答率(トレーニング) = 0.92
: 1000. 正答率(テスト) = 0.92
```

- 学習率を0.1->0.4(テスト正答率0.94)->0.6(テスト正答率0.96)
バタつきながら早く最適な解に落ち着いている。大体予想した通りの動き。

- 出力層のノード変更→エラーが出る。正解の数は決まっている。
```
d_train.shape
(60000, 10)
```
- 中間層サイズの変更→サイズを大きくしても特に精度は良い方向にいかない。
層を増やす方が表現力が増すのかもしれない。
- 入力層の数を増やす→エラーが出る。入力のサイズは決まっている。
```
x_train.shape
(60000, 784)
```
### 確認テスト
**誤差逆伝播法では不要な再帰的処理を避ける事が出来る。
既に行った計算結果を保持しているソースコードを抽出せよ。**
1_2_back_propagation.ipynb
```python=
# 誤差逆伝播
def backward(x, d, z1, y):
print("\n##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = functions.d_sigmoid_with_loss(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
print_vec("偏微分_dE/du2", delta2)
print_vec("偏微分_dE/du2", delta1)
print_vec("偏微分_重み1", grad["W1"])
print_vec("偏微分_重み2", grad["W2"])
print_vec("偏微分_バイアス1", grad["b1"])
print_vec("偏微分_バイアス2", grad["b2"])
return grad
```
答えでは
1_3_stochastic_gradient_descent.ipynb
の方のbackward関数
---
**1 $\displaystyle \frac{\partial E}{\partial y}\frac{\partial y}{\partial u}$**
**2 $\displaystyle \frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\frac{\partial u}{\partial w_{ij}^{(2)}}$**
**二つの空欄に該当するコードを探せ**
1_3_stochastic_gradient_descent.ipynbより
1. ```delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)```
2. ```grad['W1'] = np.dot(x.T, delta1)```
---
### その他関連事項
---
プロローグより
**データ集合の拡張**
(Dataset Augumentation)
https://www.deeplearningbook.org/contents/regularization.html
人工的にデータを水増しする。
画像の分類タスクに使われる
回転、拡大、縮小、+ノイズなど
データ拡張の結果、データセット内で混同するデータが発生しないように注意
ニューラルネット内のノイズ注入によるデータ拡張
中間層にノイズを注入する。
データを拡張を行うとしばしば劇的に汎化性能が向上する
ランダムなデータ拡張を行うときは学習データが毎度異なるため再現性に注意
密度推定のためのデータも水増しはできない。
---
# 深層学習day2
## 1.勾配消失問題
### 要約
中間層を増やしていくと生じる問題
うまく学習できない事がある。
微分の連鎖律を用いながら重みの更新量を求めてきた。
入力層に近づくにつれて微分の数が増えてくる
入力層に近い方でパラメータが更新されなくなる。
微分値0から1の値をとるものが多い。
=かければかけるほど値が小さくなってしまう。0.5x0.5x0.5x.....
活性化関数をシグモイド関数にした例:
ゼロ付近でyが0から1に上がる
シグモイド関数を微分すると。。。x=0付近でyが**最高で0.25**になる山形。
これが増えていくとゼロに近くなってしまう。
- 解決方法
- 活性化関数の選択
- 重みの初期値設定
- バッチ正規化
#### 活性化関数の選択
- ReLU関数
$f(x) = \left\{
\begin{array}{ll}
x & (x > 0) \\
0 & (x \leq 0)
\end{array}
\right.$
0より小さい時は微分は0、1以上の時は微分は1
連鎖律上に0があると使われなくなる。1があるとそのまま使われる(選択的)
1はいくら掛けても1なので勾配消失問題は解消される
0が入ると不必要な重みは更新されない→結果的に必要的な部分のみ更新される(スパース化)
#### 初期値の設定方法
重みの初期値としてはランダムな値を入れる。
偏りのない状態でスタートして色んなタイプを試す。
- 重みの初期値設定:Xavier
重みの要素を前のノードの数の平方根で除算した値
S字型の活性化関数を用いる時にいい感じになる
標準正規分布でランダムな初期値にした場合、中間層の出力→0、1付近が多い
標準偏差を0.01にした正規分布 全ての真ん中による
Xavierの出力 ばらつきがあって表現力がある
- Relu関数の場合: He
重みの要素を前の層のノード数の平方根で除算した値に対し$\sqrt 2$を掛け合わせた値
```network['W1']=np.random.randn(input_layer_size,hidden_layer_size)/np.sqrt(input_layer_size)*np.sqrt(2) ```
2_2_2_vanishing_gradient_modified.ipynb 参照
#### バッチ正規化
ミニバッチ単位で入力値のデータの偏りを抑制する手法
学習時のミニバッチ毎に各チャンネルを平均0分散1になるように正規化する
$N_{t}$: バッチあたりの枚数
$\displaystyle \mu_{t}=\frac{1}{N_{t}}\sum_{i=1}^{N_{t}} x_{ni}$: ミニバッチ 全体の平均
$\displaystyle \sigma_{t}^{2}=\frac{1}{N_{t}}\sum_{i=1}^{N_{t}}(x_{ni}-\mu_{t})^{2}$ :ミニバッチの分散
$\displaystyle \hat x_{ni}=\frac{x_{ni}-\mu_{t}}{\sqrt {\sigma_{t}^{2}+\theta}}$ :ミニバッチの正規化
$y_{ni}=\gamma x_{ni} + \beta$:扱いやすいように係数とバイアスを付加
2_2_2_vanishing_gradient_modified.ipynb
2_3_batch_normalization.ipynb
```python=
if train_flg:
mu = x.mean(axis=0) # 平均
xc = x - mu # xをセンタリング
var = np.mean(xc**2, axis=0) # 分散
std = np.sqrt(var + 10e-7) # スケーリング
xn = xc / std
self.batch_size = x.shape[0]
self.xc = xc
self.xn = xn
self.std = std
self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu # 平均値の加重平均
self.running_var = self.momentum * self.running_var + (1-self.momentum) * var #分散値の加重平均
```
### 実装演習結果サマリー、考察
**2_1_network_modified.ipynb**

**2_2_1_vanishing_gradient.ipynb**
**ReLU-gauss**
```
Generation: 1980. 正答率(トレーニング) = 0.9
: 1980. 正答率(テスト) = 0.9118
Generation: 1990. 正答率(トレーニング) = 0.89
: 1990. 正答率(テスト) = 0.9132
Generation: 2000. 正答率(トレーニング) = 0.89
: 2000. 正答率(テスト) = 0.9086
```

**sigmoid-Xavier**
```
Generation: 1980. 正答率(トレーニング) = 0.77
: 1980. 正答率(テスト) = 0.7747
Generation: 1990. 正答率(トレーニング) = 0.74
: 1990. 正答率(テスト) = 0.7807
Generation: 2000. 正答率(トレーニング) = 0.72
: 2000. 正答率(テスト) = 0.7846
```

**Relu-He**
```
Generation: 1980. 正答率(トレーニング) = 0.98
: 1980. 正答率(テスト) = 0.9507
Generation: 1990. 正答率(トレーニング) = 0.96
: 1990. 正答率(テスト) = 0.9505
Generation: 2000. 正答率(トレーニング) = 0.95
: 2000. 正答率(テスト) = 0.948
```

**2_2_2_vanishing_gradient_modified.ipynb**
- sigmoid, relu: 活性化関数
- Xavier, He:重み初期値の割り当て方法
の組み合わせ
**[try] hidden_size_listの数字を変更してみよう**
[40, 20]→[60, 20] やや正答率が上がった。
```
Generation: 1980. 正答率(トレーニング) = 1.0
: 1980. 正答率(テスト) = 0.9577
Generation: 1990. 正答率(トレーニング) = 0.96
: 1990. 正答率(テスト) = 0.9614
Generation: 2000. 正答率(トレーニング) = 1.0
: 2000. 正答率(テスト) = 0.9601
```

**[try] sigmoid - He と relu - Xavier についても試してみよう**
**sigmoid-He**
```
Generation: 1980. 正答率(トレーニング) = 0.87
: 1980. 正答率(テスト) = 0.8894
Generation: 1990. 正答率(トレーニング) = 0.94
: 1990. 正答率(テスト) = 0.8886
Generation: 2000. 正答率(トレーニング) = 0.89
: 2000. 正答率(テスト) = 0.8894
```

**relu-Xavier**
```
Generation: 1980. 正答率(トレーニング) = 0.98
: 1980. 正答率(テスト) = 0.9509
Generation: 1990. 正答率(トレーニング) = 0.98
: 1990. 正答率(テスト) = 0.9521
Generation: 2000. 正答率(トレーニング) = 0.95
: 2000. 正答率(テスト) = 0.9483
```

全般的に最終的な精度はsigmoidよりReluの方が良い値が出ている。
また学習の進みも早い。
### 確認テスト
**連鎖率の原理を使い、dz/dxを求めよ**
$z=t^{2}$
$t=x+y$
→$\displaystyle \frac{\partial z}{\partial t}\frac{\partial t}{\partial x}$
→$\displaystyle 2t \cdot 1$→$2t$
答え
最後$2(x+y)$で終わらせる
**シグモイド関数を微分した時、入力値が0の時に最大値をとる。その
値として正しいものを選択肢から選べ**
**1. 0.15, 2. 0.25, 3. 0.35, 4. 0.45**
答え
2.
$\displaystyle f(u)=\frac{1}{1+e^{-u}}$
$f'(u)=(1-f(u))\cdot f(u)$
**重みの初期値に0を設定するとどのような問題が発生するか、簡潔に述べよ**
該当するパスでは伝播しない
答え
(多分伝播しないというわけではない。biasもあるし。ただ意味がない。)
重みを0で初期化すると正しい学習が行えない→すべての重みの値が均一に更新されるため
多数の重みを持つ意味がなくなる。
**一般的に考えられるバッチ正規化の効果を2点挙げよ**
- 中間層の重みの更新の安定化、学習が早い
- データに偏りができにくいので過学習が防げる
### その他関連事項
アフィン変換=画像回転とかで出てくる行列計算に似たもの
アフィン層は同様の計算をしているのでアフィン層と呼ばれている。
活性化関数までは含まない。
参考文献:ゼロからつくるDeep Learning P186-189
## 2.学習率最適化手法
### 要約
**復習**
$\epsilon$:学習率
$w^{(t+1)}=w^{(t)}-\epsilon\nabla E$
$\displaystyle \nabla E= \frac{\partial E}{\partial \boldsymbol w} = [\frac{\partial E}{\partial w_{1}},,,\frac{\partial E}{\partial w_{M}}]$
学習率の値が大きい→最適値にたどり着かず発散
学習率の値が小さい→発散する事はないが、小さすぎると収束するまでに時間がかかってしまう。
大域的局所最適値に収束しずらくなる
#### モメンタム
VはWと一緒。$V_{t-1}$は前回学習時の重み
前回の学習の重みに慣性値を掛けたものから、誤差を重みで微分したものを学習率でかけたものから引く。
$\displaystyle V_{t}=\mu V_{t-1}-\epsilon \nabla E$
$\boldsymbol w^{(t+1)} =\boldsymbol w^{(t)}+V_{t}$
慣性: $\mu$
```python
self.v[key]=self.momentum*self.v[key]-self.learning_rate*grad[key]
params[key]+=self.v[key]
```
モメンタムのメリット
- 局所的最適化にはならず、大域的最適解となる
- 谷間についてから最も低い位置(最適解)にいくまでの時間が早い
Momentumは下りに入ってから早い
https://github.com/Jaewan-Yun/optimizer-visualization/blob/master/figures/movie11.gif より

#### AdaGrad
$h_{0}=\theta$ :最初は適当な値
$h_{t}=h_{t-1}+(\nabla E)^{2}$
$\displaystyle \boldsymbol w^{(t+1)}=\boldsymbol w^{t}-\epsilon \frac{1}{\sqrt{h_{t}+\theta}}\nabla E$
```python
self.h[key]=np.zeros_like(val)
self.h[key]+=grad[key]*grad[key]
params[key]-=self.learning_rate*grad[key]/(np.sqrt(self.h[key])+1e-7)
```
メリット
勾配の緩やかな斜面に対して最適値に近づける
課題
学習率が徐々に小さくなるので、**鞍点問題**を引き起こす事があった。
https://camo.githubusercontent.com/cccdc200cc2a3052ad9562f6f58ebd429d634fb1190a84b20db931e8ad4ffb8f/68747470733a2f2f692e737461636b2e696d6775722e636f6d2f316f6274562e676966 より

鞍点:ある方向から見ると極大値、別の方向から見ると極小値
#### RMSProp
$h_{t}=\alpha h_{t-1}+(1-\alpha)(\nabla E)^{2}$
AdaGradとの違い。
前回までの経験$h_{t-1}$をどれくらい($\alpha$)生かすか,
今回の経験を($1-\alpha$)生かすか。バランス取れる。
$\displaystyle \boldsymbol w^{(t+1)}=\boldsymbol w^{t}-\epsilon \frac{1}{\sqrt{h_{t}+\theta}}\nabla E$
```python
self.h[key] *= self.decay_rate
self.h[key] += (1-self.decay_rate) * grad[key] * grad[key]
params[key]-=self.learning_rate*grad[key]/(np.sqrt(self.h[key])+1e-7)
```
メリット
- 局所的最適解にはならず、大域的最適解となる
- ハイパーパラメータの調整が必要な場合がすくない。
#### Adam
モメンタムの過去の勾配の指数関数的減衰平均、
RMPSPropの過去の勾配の2乗の指数関数的減衰平均
を含めた最適化
モメンタム、RMSPropのメリットを孕んだアルゴリズムである
2_4_optimizer.ipynb
```python
if i == 0:
m[key] = np.zeros_like(network.params[key])
v[key] = np.zeros_like(network.params[key])
m[key] += (1 - beta1) * (grad[key] - m[key])
v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])
network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)
```
### 実装演習結果サマリー、考察
**2_4_optimizer.ipynb**
RSMProp
```
Generation: 980. 正答率(トレーニング) = 0.96
: 980. 正答率(テスト) = 0.939
Generation: 990. 正答率(トレーニング) = 0.96
: 990. 正答率(テスト) = 0.9385
Generation: 1000. 正答率(トレーニング) = 0.99
: 1000. 正答率(テスト) = 0.9411
```

Adam
```
Generation: 980. 正答率(トレーニング) = 0.95
: 980. 正答率(テスト) = 0.9413
Generation: 990. 正答率(トレーニング) = 0.97
: 990. 正答率(テスト) = 0.9471
Generation: 1000. 正答率(トレーニング) = 0.95
: 1000. 正答率(テスト) = 0.9498
```

それほどの違いは見られないが、ややAdamの方がいい精度が出ている
**[try]学習率を変えてみよう**
Adamに関して学習率を0.01->0.08

行ったり来たりを繰り返して最小の箇所にたどり着けない
**[try] 活性化関数と重みの初期化方法を変えてみよう**
Adamにおいて重み初期値の設定をxavier,活性化関数をReluにした所、
もう少し精度が上がった。
```
Generation: 980. 正答率(トレーニング) = 0.97
: 980. 正答率(テスト) = 0.9473
Generation: 990. 正答率(トレーニング) = 0.99
: 990. 正答率(テスト) = 0.9512
Generation: 1000. 正答率(トレーニング) = 0.97
: 1000. 正答率(テスト) = 0.9513
```

**[try] バッチ正規化をしてみよう**
前に学習がうまくいかなかった**AdaGrad**について
バッチ正規化なし

バッチ正規化あり(効果が見られる)

### 確認テスト
講義の中ではなし
### その他関連事項
**バッチ正規化についてもう少し**
参考文献:セロから作るDeepLearning (P187-P189)
- 初期値についても言及している。利点として初期値にそれほど依存しない。(あまり神経質にならなくて良い)
(「初期値にロバスト」と表現している)
- Batch正規化を使わないと全く学習が進まないケースもあり。ほとんどの場合で
サンプル内では効果が出ている。
データ分布の偏りをなくす事の効果が大きい。
逆伝播の際はどう取り扱うかについては処理を追わなかった。
## 3.過学習
### 要約
テスト誤差と訓練誤差とで学習曲線が乖離する事
特定の訓練サンプルに対して特化して学習する
原因:
(入力の数に対して)パラメータの数が多い
パラメータの値が適切でない
ノードが多い
見分け方
訓練誤差がOKで
テスト誤差がNG。
また訓練誤差が1だと怪しい
#### L1、L2正則化、ドロップアウト
ニューラルネットワークの自由度が高い、高すぎると過学習が起こる
正則化とはネットワークの自由度(層数、ノード数、パラメータ数、etc)を制約する事
→**正則化手法**を利用して過学習を抑制する
ドロップアウトも正則化と言える
- **L1,L2正則化**
過学習が起きている時にニューラルネットの中では何が起きているか?
重みが大きくなっている事で過学習が起きることがある。
重みが大きい→入力された情報の中で重要な箇所である所
重み大きすぎる→過大評価 一部の入力データに対し極端な反応を示してしまう。
誤差に対して正則化項を加算した上で重みを抑制する。
過学習が起こりそうな重みの大きさ以下で重みをコントロールし、かつ
重みの大きさにバラつきを出す必要がある。
$\displaystyle E_{n}(\boldsymbol w)+\frac{1}{p}{\lambda}\|x\|_{p}$ : 誤差関数にpノルムを加える
$\lambda$:ハイパーパラメータ
```
weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))
loss = network.loss(x_batch, d_batch + weight_decay
```
$\displaystyle \|x\|_{p}=(|x_{1}|^{p}+...+|x_{n}|^{p})^{\frac{1}{p}}$ : pノルムを加える
```
np.sum(np.abs(network.params['W' + str(idx)]))
```
p=1(p1ノルム)の場合、L1正則化→**Lasso回帰**
p=2(p2ノルム)の場合、L2正則化→**リッジ回帰**
ノルム・・・距離
p1ノルム:マンハッタン距離 $x+y$
p2ノルム:ユーグリット距離 $\sqrt{x^{2}+y^{2}}$
誤差関数に正則化項をプラスして変化させている
- **ドロップアウト**
- 課題:ノードの数が多い
- ランダムにノードの数を削除して学習する事
- データ量を変えずに異なるモデルを学習させていることになる
### 実装演習結果サマリー、考察
**2_5_overfiting.ipynb**
わざと過学習を起こしているスクリプト

L2の適用 訓練データに限れは正答率1から下がって汎化能力が
上がっているように見えるがテストデータに対しては実際あまり効果が出ていない。

L1の適用
重みが途中で消えるような状態。

Dropout
進みが遅いが順調に進んでいるように見える。
Dropoutによって実質データが増えたのと同じ事になる。

Dropout+L1

**[try] weigth_decay_lambdaの値を変更して正則化の強さを確認しよう**
L2 weight_decay_lambda 0.1->0.3
大きく抑制されているのが分かる。

**[try] dropout_ratioの値を変更してみよう**
現在の0.15が大体良い所。
### 確認テスト
**下図においてL1正則化を表しているグラフはどちらか答えよ**
よく出てくる絵。今まであまりよく意味が分からなかった。
グルグルしている所が誤差関数を上から見た等高線。
中央の円が正則化項を切り取った等高線図。
**二つが触れている箇所が、誤差関数+正則化項でもっとも低くなる場所**
Lassoの方はもっとも低くなるところで一つの重みがゼロになっている
→**スパース化につながる**
答え:
右のLassoの方
### 例題チャレンジ
L2パラメータ正則化
正解: param
L1パラメータ正則化
正解:signn(param)
### その他関連事項
Dropoutについて追加
参考文献:ゼロから作るDeepLearning P195-197
訓練時にはランダムに消去するニューロンを選ぶが、
テスト時は全てのニューロンの信号を伝達するが、各ニューロンの出力に対して
訓練時に消去した割合を乗算して出力する。
表現力の高いネットワークでも過学習を抑制する事ができる
## 4.畳み込みニューラルネットワークの概念
### 要約
次元間でつながりのあるデータを扱える。
画像。ある点で隣の点と大体同じ色の可能性が高い
音声。大体前の音とつながりがある
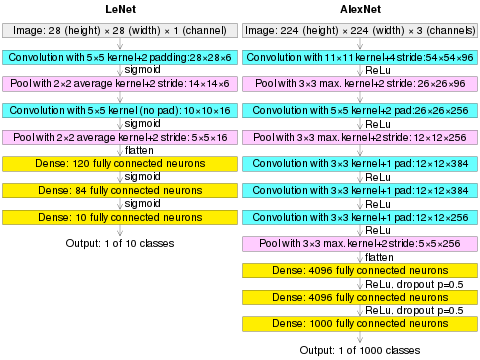
- Lenet
- Input 32x32, output 10種類に分類
- 32x32=1024個を10個に
http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf

```
(32, 32) 1024個 → (28, 28, 6) 4704個 → (14, 14, 6) 1176個
→(10, 10, 16) 1600個 →(5, 5, 16) 400個 → (120,) 120個 → (84,) 84個
→(10,) 10個
```
- 畳み込み層
入力値
大体3ch(RGB)
入力値 * フィルター → 出力値、バイアス、活性化関数、→ 出力値
フィルターを動かしながら、まわりの情報を取り込みながら変換する事で
つながりを保っている。
上記前半の複数の次元を保っている所、特徴量の抽出機能。
特徴量を元に欲しい値を得る(全結合層)
全結合での学習=隣接する全てのニューロン間でつながりがある
畳み込み層では画像の場合、縦、横、チャンネルの3次元のデータをそのまま
学習し、次に伝える事ができる。
フィルタ自体が全結合でいう重みに該当。
(このフィルタで画像を読み取ったらどうなるか?)
- フィルタを通してバイアスを足す
- 画像が小さくなってしまうのを防ぐために**パディング**をする
(入力画像に前もって0で穴埋めとか)
- フィルタをどれだけ動かすか、ずらすかは**ストライド**
- チャンネルは**フィルタの数**(何人で読み込むか)
- プーリング層
- ずれながら対象領域のMax値、または平均値を取得
- Max Pooling, Avg Pooling
#### プログラム確認
---
2_6_simple_convolution_network_after.ipynb
```python=
# レイヤの生成
self.layers = OrderedDict()
self.layers['Conv1'] = layers.Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = layers.Relu()
self.layers['Pool1'] = layers.Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = layers.Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = layers.Relu()
self.layers['Affine2'] = layers.Affine(self.params['W3'],self.params['b3'])
```
画像を読み込む際の工夫
https://medium.com/@_init_/an-illustrated-explanation-of-performing-2d-convolutions-using-matrix-multiplications-1e8de8cd2544
フィルタを適用する範囲を前もって一列ないしは一行にまとめる

---
**プーリング層の実装部分**
2_6_simple_convolution_network_after.ipynb
```python=
# xを行列に変換
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
# プーリングのサイズに合わせてリサイズ
col = col.reshape(-1, self.pool_h*self.pool_w)
#maxプーリング
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
```
---
### 実装演習結果サマリー、考察
**2_6_simple_convolution_network.ipynb**
```
Generation: 980. 正答率(トレーニング) = 0.9966
: 980. 正答率(テスト) = 0.963
Generation: 990. 正答率(トレーニング) = 0.9924
: 990. 正答率(テスト) = 0.964
Generation: 1000. 正答率(トレーニング) = 0.9948
: 1000. 正答率(テスト) = 0.961
```

良い精度が出ている
### 確認テスト
**サイズ6x6の入力画像を、サイズ2x2のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なおストライドとパディングは1とする**
6+2-2=6
ストライドは1なので出力サイズはそのまま~~6x6~~
→×最後にプラス1するから7x7
公式としては
1辺(高さor幅)=$\displaystyle \frac{画像の高さ+2\times パディング-フィルター高さ}{ストライド}+1$
数えた方が早いかもしれない
### その他関連事項
なし
## 5.最新のCNN
### 要約
- 初期AlexNet
- 特徴量から結合層への移行
- (13, 13, 256)
- Flatten・・・一列に並べる [43264個]
- Global Max Pooling [13x13で一番大きな値 256個]
- Global Avg Pooling [13x13で平均の値 256個]
- 各チャンネル(面)の画素平均を求め、それをまとめます
- 過学習を防ぐ施策
- サイズ4096の全結合層の出力にドロップアウトを使用している
https://en.wikipedia.org/wiki/AlexNet
他の ネットワーク
- **VGG**
- 畳み込み層とプーリング層から構成される基本的なCNN
- 重みのある層数に応じてVGG16,VGG19がある
- 3x3の小さめフィルター
- **GoogLeNet**
- 特徴的なインセプション構造
- サイズの異なるフィルタとプーリングを複数適用し、その結果を結合する
- *これまでのアーキテクチャは、畳み込み層を順列に繋げていた。このため、畳み込み層が深くなるにつれ、画像サイズが小さくなっていき、層を深くすることができなかった。これに対して、GoogLeNet では、1 つの入力画像に対して、複数の畳み込み層(1×1, 3×3, 5×5)を並列に適用し、それぞれの畳み込み計算の結果を最後に連結している。この一連の作業をモジュールとしてまとめられ、Inception モジュールと呼ばれている。Inception モジュールを多数使うことで、パラメーターが膨大な数になる。そこで、GoogLeNet では、各畳み込み計算を行う前に 1×1 Convolution を行い、パラメーター数を削減している。*
- **ResNet**
- 層を深くしすぎると学習がうまくいかない事を解消するために
スキップ構造(「ショートカット」、「バイパス」)を導入
- 入力データの畳み込み層をスキップして出力に合算
他トピックとして
演算制度のビット削減について興味深い記述があった。
ネットワークを流れるデータの精度(ビット数)はそれほど求められない。
DeepLearningにおいては16ビットの半精度浮動小数点でも十分学習できる
参考文献:ゼロからつくるDeepLearning、イラストでまなぶディープラーニング
### 実装演習結果サマリー、考察
**2_7_double_comvolution_network.ipynb**
```
Generation: 80. 正答率(トレーニング) = 0.7386
: 80. 正答率(テスト) = 0.715
Generation: 90. 正答率(トレーニング) = 0.8058
: 90. 正答率(テスト) = 0.765
Generation: 100. 正答率(トレーニング) = 0.8224
: 100. 正答率(テスト) = 0.782
```

**2_8_deep_convolution_net.ipynb**
学習時間は30分ほど良い精度が出ている
```
Generation: 980. 正答率(トレーニング) = 0.9958
: 980. 正答率(テスト) = 0.984
Generation: 990. 正答率(トレーニング) = 0.996
: 990. 正答率(テスト) = 0.986
Generation: 1000. 正答率(トレーニング) = 0.993
: 1000. 正答率(テスト) = 0.981
```

### その他関連事項
データセット
- **ImageNet**
- 100万枚を超えるデータセット
- 動物、植物、食べ物
- **Places**
- 風景、乗り物、建物など
- **COCO**
- 物体認識だけでなく、セグメンテーションや画像要約などにも使える
- 80クラス、20万枚のサンプル
- **Open Images Dataset V4**
- Google公開の大規模データセット
- 学習用に900万枚、検証用とテスト用にそれぞれ約4万枚、12万枚
### 他メモ
**入力層の設計**
入力層として取るべきでないデータ
- 欠損値が多いデータ
- 誤差の大きいデータ
- 出力そのもの、出力を加工した情報
- end-to-end
- 連続性のないデータ
- 無意味な数が割り当てられているデータ
欠損値の扱い
- ゼロで埋める
- 入力値(特徴量)として採用しない
- 欠損値を含む集合を除外
数値の正規化(1-0に収める)、正則化(平均ゼロ、分散1)
データの結合
**CNNで扱えるデータの種類**
https://www.deeplearningbook.org/contents/convnets.html
https://www.cs.toronto.edu/~kriz/cifar.html
https://products.sint.co.jp/aisia/blog/vol1-6
次元間でつながりのあるデータ
| | 1次元 | 2次元 | 3次元 |
| -------- | -------- | -------- |----- |
| 単一チャンネル | 音声 | フーリエ変換した音声 | CTスキャン画像 |
| 複数チャンネル| アニメのスケルトン | カラー画像 | 動画 |
---
**特徴量の転移**
https://www.deeplearningbook.org/contents/representation.html
https://www.mi.t.u-tokyo.ac.jp/research/domain_adaptation/
one-shot learnig
zero-shotlearning, sometimes also called zero-data learning
Multimodal learning
---
**転移学習**
入力層に近いところはデータの基本的な特徴を捉えている
ゼロベースの学習
ファインチューニング・・・学習済み重みを再学習
転移学習・・・学習済み重みをそのまま使う
学習済み重み(ベースモデル)・・・大量のデータを使って学習されたもの。プリトレーニングという。教師なし学習を行う。
特徴量抽出 タスク固有処理
VGG(画像),BERT(テキスト)
---
問題より
- Leave-one-out 交差検証
データを一つ抜き出して検証データとし、それ以外を訓練データとして学習する。
全てのデータが一回ずつ検証対象になる。
k-分割交差における、kが標本サイズと同じになったもの。
一つ抜き法、ジャックナイフ法とも呼ばれる
**精度は高いが、時間がかかる**
参考:
https://newtechnologylifestyle.net/%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92%E3%80%81%E3%83%87%E3%82%A3%E3%83%BC%E3%83%97%E3%83%A9%E3%83%BC%E3%83%8B%E3%83%B3%E3%82%B0%E3%81%A7%E3%81%AE%E5%AD%A6%E7%BF%92%E3%83%87%E3%83%BC%E3%82%BF%E3%81%A8/
---
主成分分析
再構成誤差
https://ichi.pro/shuseibun-bunseki-143655518282726
---
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet