345 Notes - Determinants and Volume
==============
###### tags: `345` `linear algebra`

As a warm up here is a [nicely illustrated video from 3Blue1Brown](https://youtu.be/Ip3X9LOh2dk) discussing the same aspects of determinants that I am trying to get at in these notes.
{%youtube Ip3X9LOh2dk %}

This is from the [Essence of Linear Algebra](https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab) series and [this video](https://youtu.be/kYB8IZa5AuE) might be useful in understanding the relationship between what I call the area determined by $\mathbf{u,v}\in\mathbb R^2$ and the way that the unit square determined by $\mathbf{e_1,e_2}$[^std] is *transformed* by $A$, where
$$
A=\bigl[\mathbf u\,\mathbf v\bigr]=\begin{bmatrix}u_1&v_1\\u_2&v_2\end{bmatrix}
=\bigl[A\mathbf e_1\,A\mathbf e_2\bigr]
$$
With this in mind we can think of $\bigl[\mathbf e_1\,\mathbf e_2\bigr]$ as the unit square (oriented in a particular way) and $A\bigl[\mathbf e_1\,\mathbf e_2\bigr]=\bigl[A\mathbf e_1\,A\mathbf e_2\bigr]=A$ as the transformed parallelogram.

# n-dimensional volume of a [parallelepiped](https://en.wikipedia.org/wiki/Parallelepiped)
In $\mathbb{R}^n$ let $\mathbf{u_1}, \mathbf{u_2},\ldots,\mathbf{u_n}$ be $n$ vectors. These $n$ vectors uniquely determine a [parallelepiped](https://en.wikipedia.org/wiki/Parallelepiped) which we will denote $P(\mathbf{u_1},\ldots,\mathbf{u_n})$. The volume of $P(\mathbf{u_1},\ldots,\mathbf{u_n})$ will just be denoted $\text{vol}(\mathbf{u_1},\ldots,\mathbf{u_n})$.

If the vectors $\mathbf{u_1}, \mathbf{u_2},\ldots,\mathbf{u_n}$ are not independent, then the parallelepiped $P(\mathbf{u_1},\ldots,\mathbf{u_n})$ is deginerate and has a volume of 0. Conversely, if the vectors are independent, then the parallelopiped $P(\mathbf{u_1},\ldots,\mathbf{u_n})$ is non-deginerate and has a non-zero volume. This is summed up in the following fact.

**Fact:** $\text{vol}(\mathbf{u_1},\ldots,\mathbf{u_n})=0$ iff $\mathbf{u_1}, \mathbf{u_2},\ldots,\mathbf{u_n}$ are not independent.

A trivial case of this would be when $\mathbf{u_i}=\mathbf{u_j}$ for some $i\neq j$. Here we want to axiomatize volume and it is always preferable to take the weakest form of an axiom, so we adopt the following.

**Axiom 1':** $\text{vol}(\ldots,\mathbf{u},\ldots,\mathbf{u},\ldots)=0$

It turns out that directly axiomatizing volume is a bad idea since it does not behave nicely with respect to linear combinations of the vectors generating the parallelepipeds.

**Example:** In 1-dimenssion, 3 is a vector, you might think of it as the "arrow" from 0 to 3, but this is not necessary. Similarly, -3 is a vector. $P(3)$ is the 1-dimensional parallelepiped, i.e., line segment, $[0,3]$, and $\text{vol}(3)=|3|=3$. Similarly, $P(-3)$ is the line segment $[-3,0]$ and $\text{vol}(-3)=3=|-3|$.
$$
\text{vol}(3 + (-3))=\text{vol}(0)=0\neq\text{vol}(3)+\text{vol}(-3)=|3|+|-3| = 6
$$
In 1-dimension, $\text{vol}(r)=|r|$ and the example is just a case of the well-known fact that $|r+s|\leq|r|+|s|$, but in general, $|r+s|\neq |r| + |s|$.

**Example:** In $\mathbb{R}^2$, let $\mathbf{u}$ and $\mathbf{v}$, be two non-colinear vectors, so $P(\mathbf{u},\mathbf{v})$ is a non-degenerate parallelogram. Then clearly, $\text{vol}(\mathbf{u},\mathbf{v})=\text{vol}(\mathbf{-u},\mathbf{v})$, so again
$$
\begin{split}
0=\text{vol}&(\mathbf{0},\mathbf{v})=\text{vol}(\mathbf{u}+(\mathbf{-u}),\mathbf{v})\\
&\neq \text{vol}(\mathbf{u},\mathbf{v})+\text{vol}(\mathbf{-u},\mathbf{v})=2\cdot \text{vol}(\mathbf{u},\mathbf{v})>0
\end{split}
$$

These two examples suggest that if we want volume to behave nicely with respect to linear combinations of the vectors, then we need a "signed" volume, so that $\text{vol}(\mathbf{-u},\mathbf{v})=-\text{vol}(\mathbf{u},\mathbf{v})$.

# Axioms for signed volume

Here are our axioms of signed volume, $\det(\mathbf{u_1}, \mathbf{u_2},\ldots,\mathbf{u_n})$:

**Axiom 1: (multilinearity)**
$$
\begin{split}
\det(\mathbf{u_1},\ldots,&\alpha\mathbf{u_i}+\beta\mathbf{u_i}',\ldots,\mathbf{u_n})\\
&=\alpha\det(\mathbf{u_1},\ldots,\mathbf{u_i},\ldots,\mathbf{u_n})+\beta\det(\mathbf{u_1},\ldots,\mathbf{u_i}',\ldots,\mathbf{u_n})
\end{split}
$$
This is often split into two separate items.
$$
\begin{split}
\det(\mathbf{u_1},\ldots,&\mathbf{u_i}+\mathbf{u_i}',\ldots,\mathbf{u_n})\\
&=\det(\mathbf{u_1},\ldots,\mathbf{u_i},\ldots,\mathbf{u_n})+\det(\mathbf{u_1},\ldots,\mathbf{u_i}',\ldots,\mathbf{u_n})
\end{split}\tag{1}
$$
and
$$
\det(\mathbf{u_1},\ldots,\alpha\mathbf{u_i},\ldots,\mathbf{u_n})=\alpha\det(\mathbf{u_1},\ldots,\mathbf{u_i},\ldots,\mathbf{u_n})\tag{2}
$$

**Axiom 2:** $\det(\ldots,\mathbf{u},\ldots,\mathbf{u},\ldots)=0$

**Axiom 3:** $\det(\mathbf{e_1},\ldots,\mathbf{e_n})=1$

Here $\mathbf{e_i}=(0,\ldots,0,1,0,\ldots,0)$ is the unit vector in $\mathbb{R}^n$ with a 1 in the i^th^ position. So this axiom just says that the unit cube has unit volume.

Axioms 2 and 3 are clear, although Axiom 3 actually determines the "orientation" of our system of vectors and is sort of arbitrary, for example in $\mathbb{R}^2$ we have $\det((1,0),(0,1))=1$, while $\det((0,1),(1,0))=-1$.

|Illustration of Axiom 1 (1) in 2D|
|:--:|
||
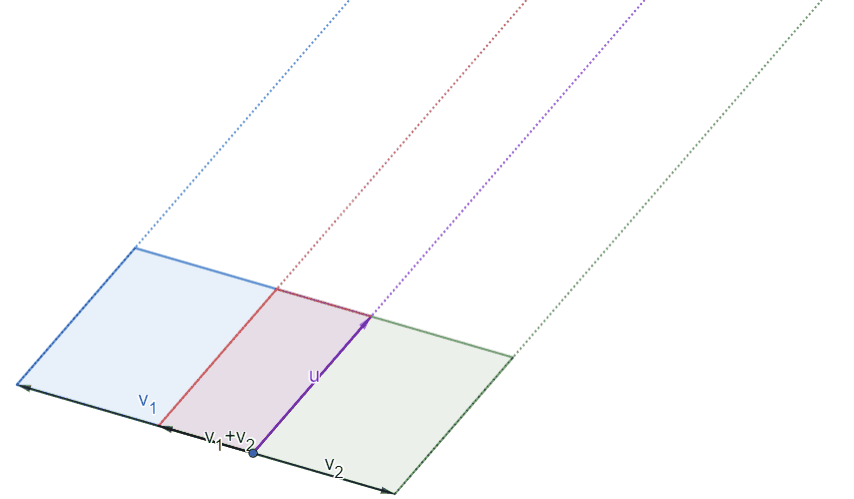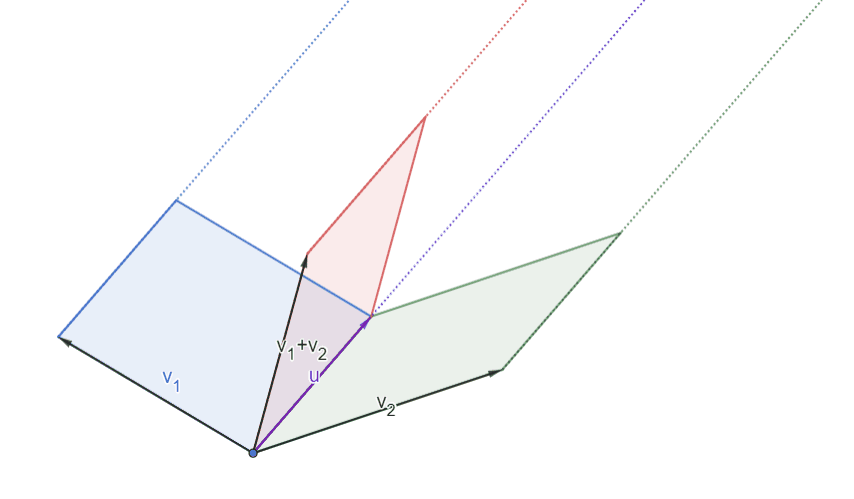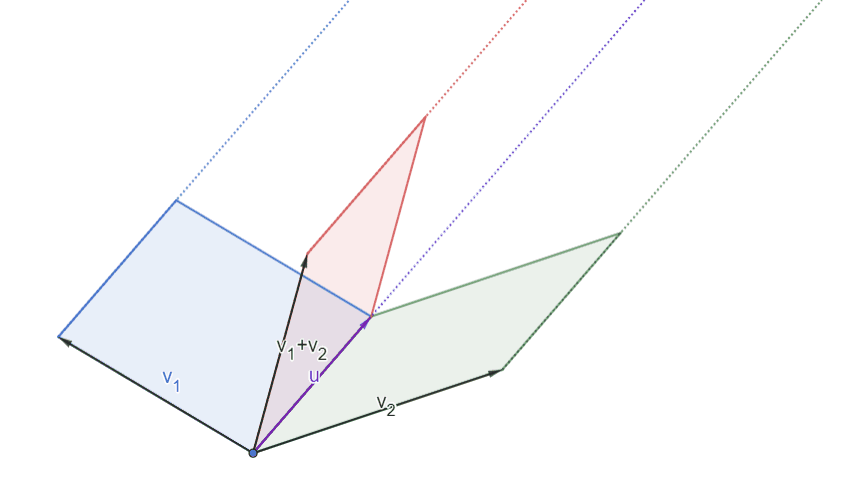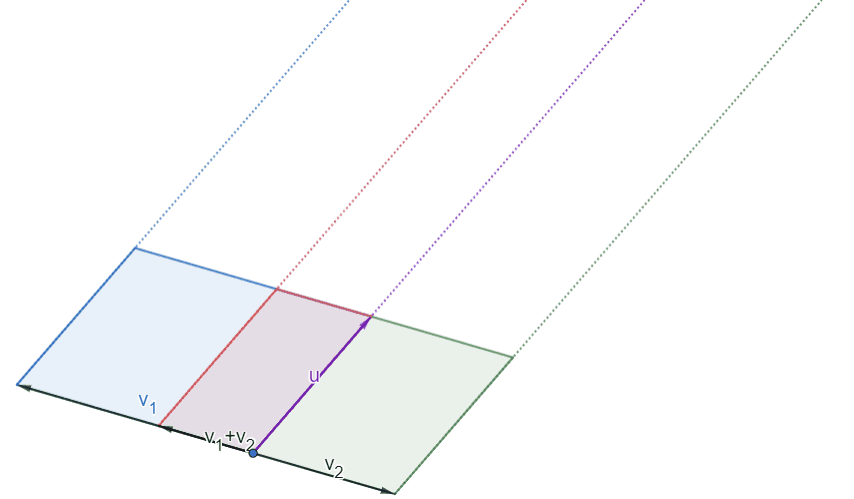|[Open in Geogebra](https://www.geogebra.org/calculator/bezhfnpw)|

:::info
Note that the areas of the three parallelograms do not change throughout the motion. From the case where $v_1$ and $v_2$ are orthogonal to $u$, it is clear that the the signed areas $\det(v_2,u)$ and $\det(v_1,u)$ result in $\det(v_1+v_2,u)$. Note also here that from the *counter-clockwise rule*, the signed areas $\det(v_1,u)<0$, $\det(v_1+v_2,u)<0$, and $\det(v_2,u)>0$.
:::

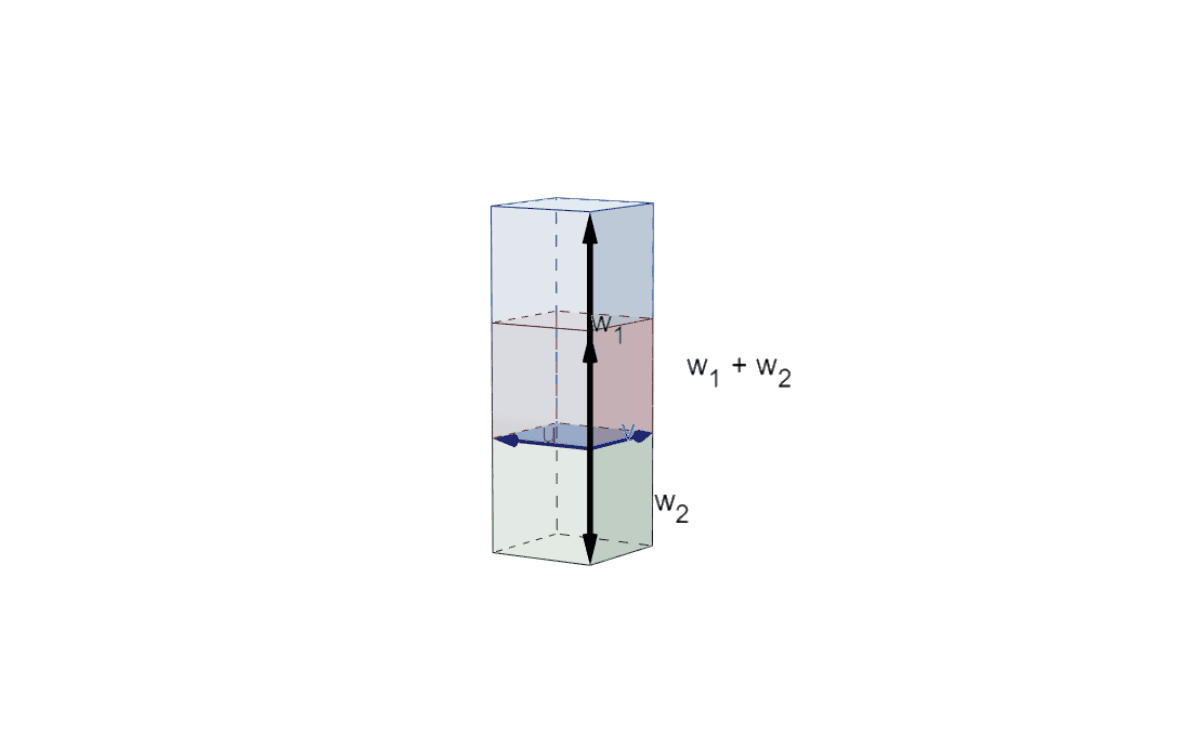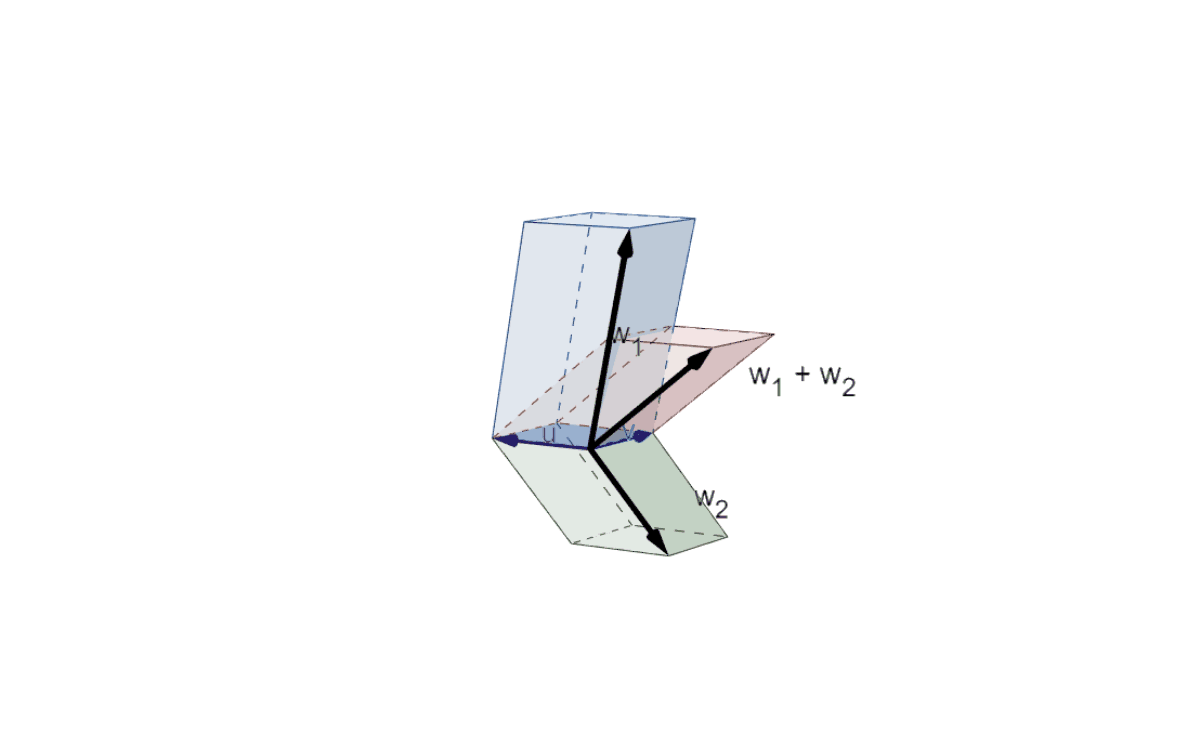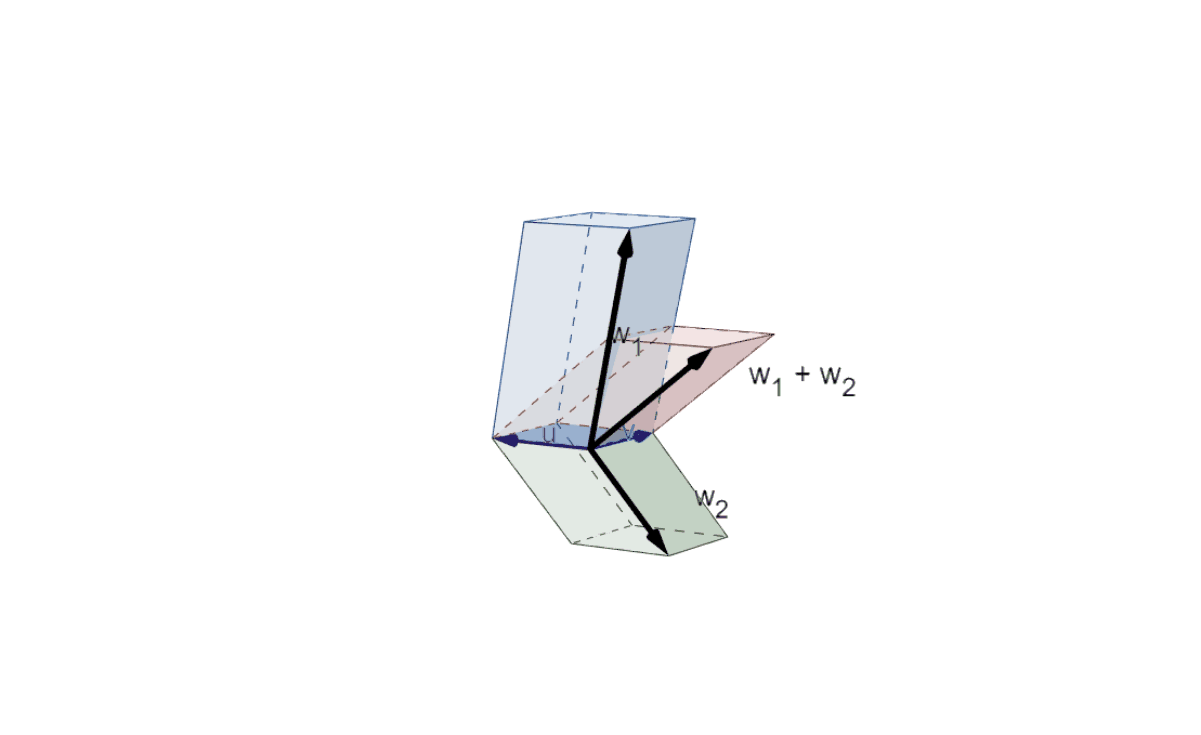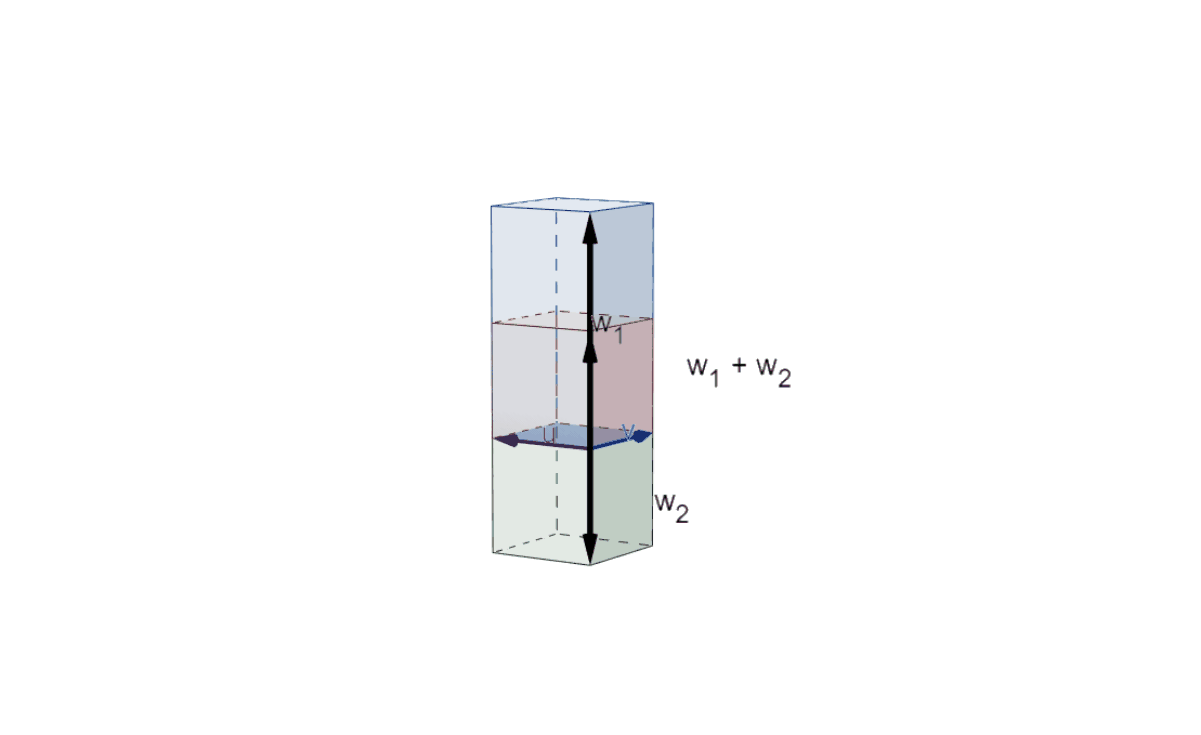
|Illustration of Axiom 1 (1) in 3D|
|:--:|
||
|[Open in Geogebra](https://www.geogebra.org/3d/ygbnxzhh)|

:::info
Similar to the situation above, the volumes of the three parallelepipeds do not change throughout their motion. From the *right-hand rule* the volumes $\det(v,u,w_1+w_2)$ and $\det(v,u,w_1)$ are positive and $\det(v,u,w_2)$ is negative. From the position where the $uv$-plane is orthogonal to the $w_i$'s it is clear that $\det(v,u,w_1)+\det(v,u,w_2)=\det(v,u,w_1+w_2)$.
:::

|Illustration of Axiom 1 (2) in 3D|
|:--:|
||
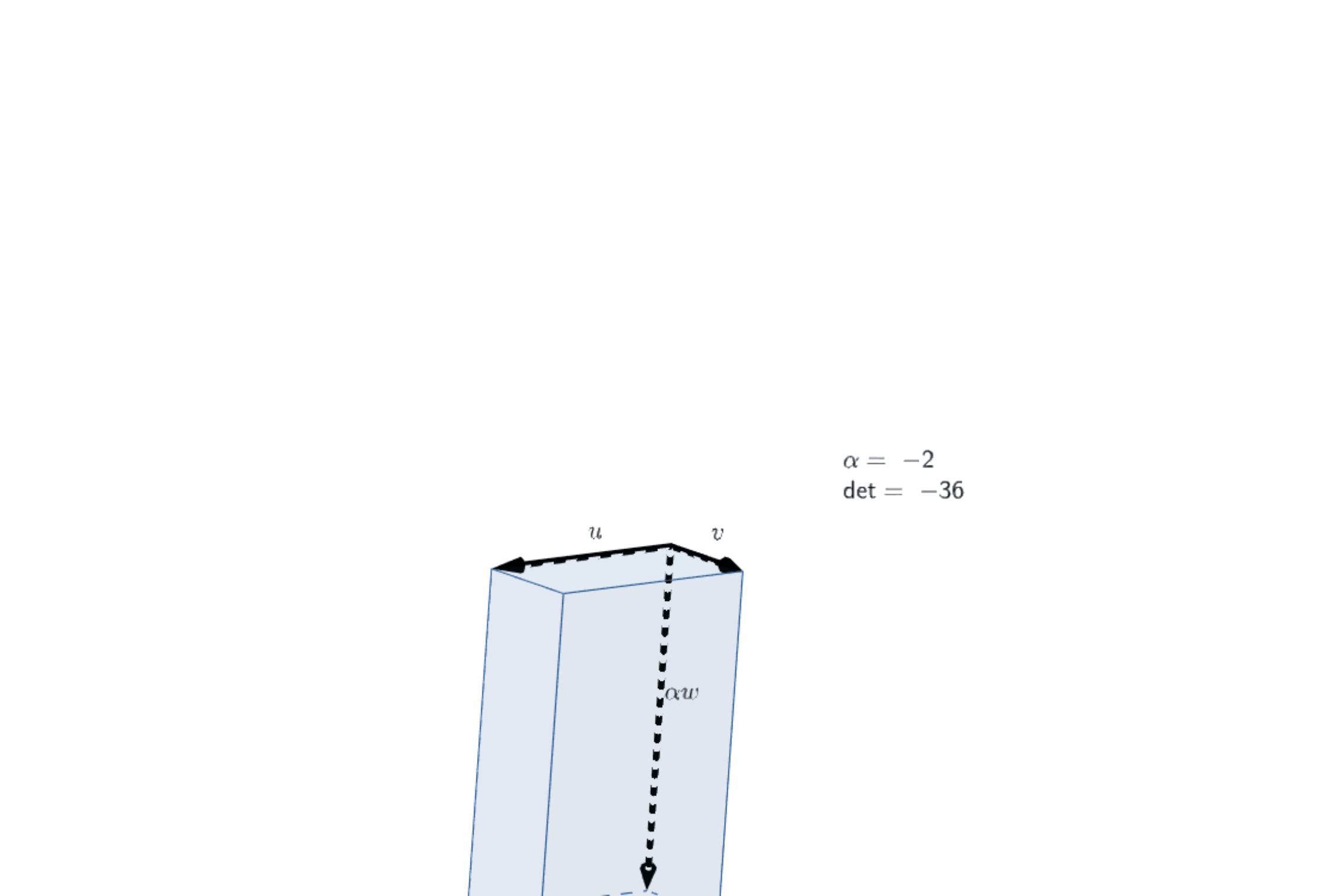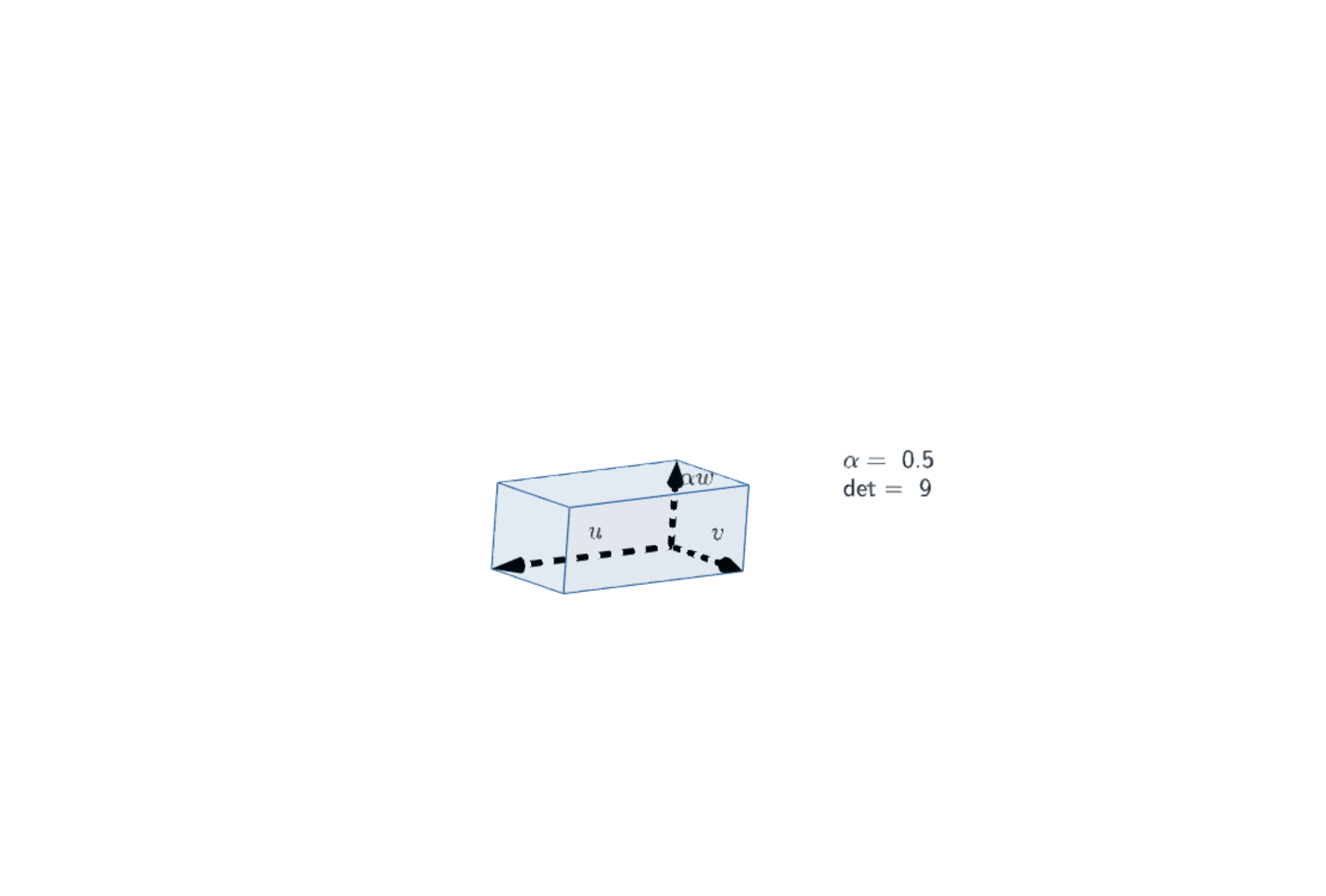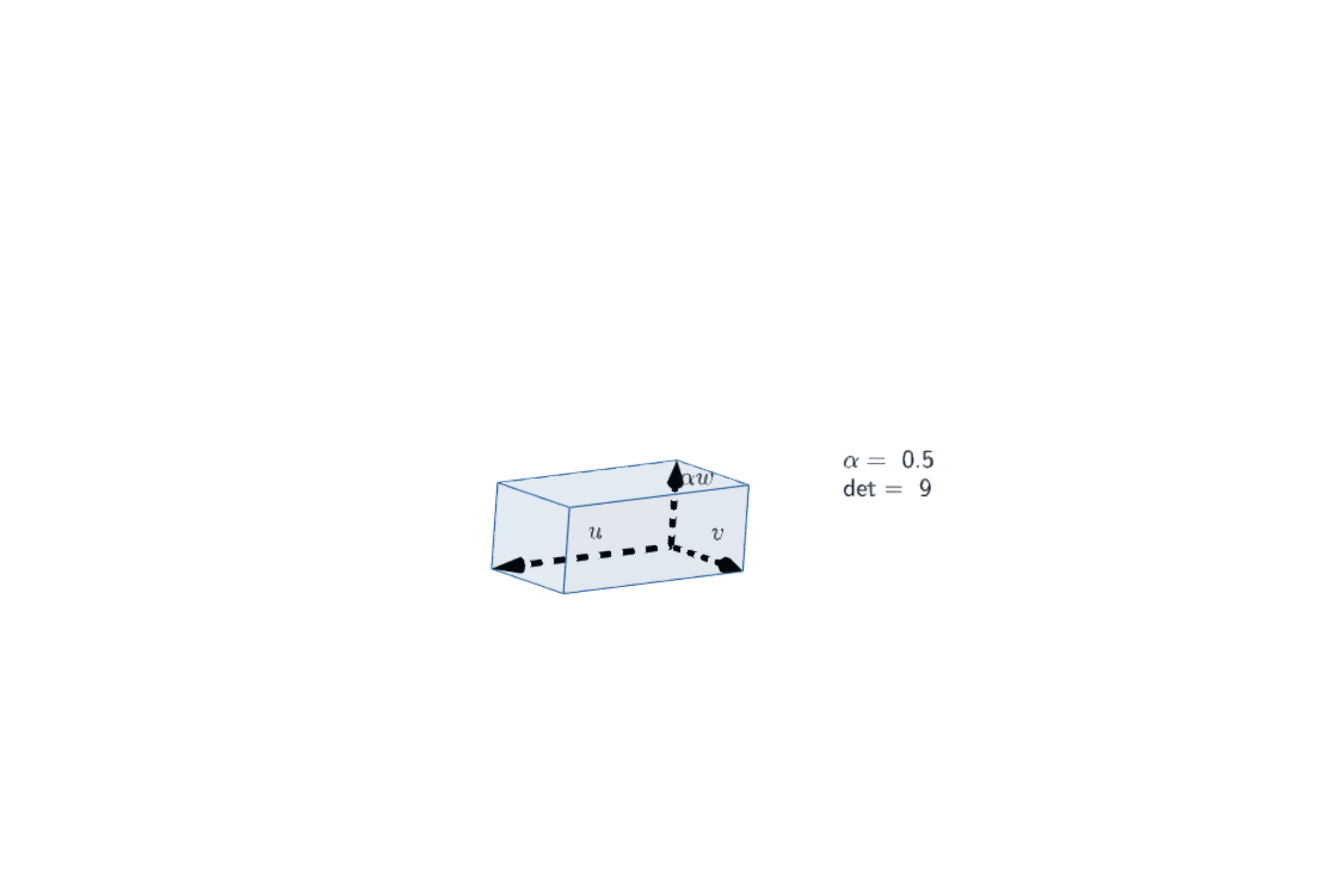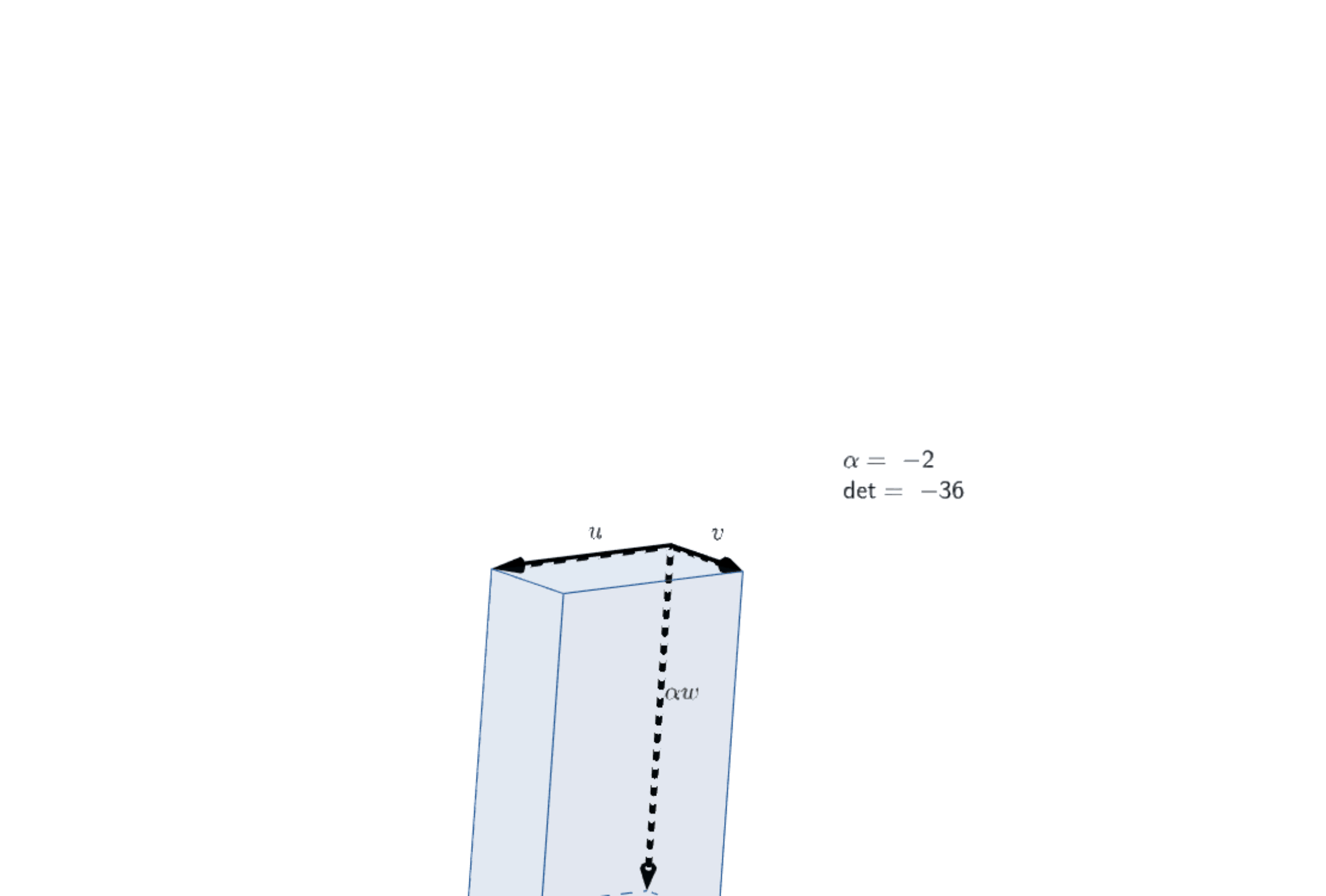|[Open in Geogebra](https://www.geogebra.org/3d/xb7cnsez)|

:::info
This image makes it clear that $\det(u,v,\alpha w)=\alpha \det(u,v,w)$, at least in $\mathbb R^3$.
:::

Part (2) of Axiom 1 is relatively clear, the tricky part is part (1), this is hinted at in the images above. Note that the various parallelepipeds *clearly* satisfy the rule when $\mathbf{v_1}$ and $\mathbf{v_2}$ are co-linear, the trick is to note that the volumes of each parallelepiped does not change and thus (2) holds also when $\mathbf{v_1}$ and $\mathbf{v_2}$ are not co-linear. The *formal* argument follows the images.

To argue formally, start with our vectors $\mathbf{u_1},\mathbf{u_2},\ldots,\mathbf{u_n}$. Let $\mathbf{n}$ be a unit normal to the hyperplane determined by the $n-1$ vectors, $\mathbf{u_2},\ldots,\mathbf{u_n}$. Let $\mathbf{w_1}=\text{proj}(\mathbf{u_1},\mathbf{n})=\langle \mathbf{u_1},\mathbf{n}\rangle\,\mathbf{n}$ be the projection of $\mathbf{u_1}$ onto $\mathbf{n}$, in other words, the *height* of the parallelepiped above the hyperplane. (In the pictures above, the hyperplane is just the *line* in the direction of $\mathbf{u}$ in the 2-dimensional picture and is the plane containing $\mathbf{u}$ and $\mathbf{v}$ in the 3-dimensional picture.) The point is
$$
\det(\mathbf{u_1},\mathbf{u_2},\ldots,\mathbf{u_n})=\det(\mathbf{w_1},\mathbf{u_2},\ldots,\mathbf{u_n})
$$
If you do the same thing for $\mathbf{u_1}'$, then we get
$$
\begin{split}
\det(\mathbf{u_1}&,\mathbf{u_2},\ldots,\mathbf{u_n})+\det(\mathbf{u_1}',\mathbf{u_2},\ldots,\mathbf{u_n})\\
&=\det(\mathbf{w_1},\mathbf{u_2},\ldots,\mathbf{u_n})+\det(\mathbf{w_1}',\mathbf{u_2},\ldots,\mathbf{u_n})\\
\end{split}
$$
Since $\mathbf{w_1}$ an $\mathbf{w_2}$ are colinear we know
$$
\begin{split}
\det(\mathbf{w_1}&,\mathbf{u_2},\ldots,\mathbf{u_n})+\det(\mathbf{w_1}',\mathbf{u_2},\ldots,\mathbf{u_n})\\
&=\det(\mathbf{w_1}+\mathbf{w_1}',\mathbf{u_2},\ldots,\mathbf{u_n})
\end{split}
$$
Finally, since the projection to $\mathbf{n}$ of $\mathbf{u_1}+\mathbf{u_2}$ is $\mathbf{w_1}+\mathbf{w_2}$ we have
$$
\det(\mathbf{w_1}+\mathbf{w_1}',\mathbf{u_2},\ldots,\mathbf{u_n})=\det(\mathbf{u_1}+\mathbf{u_1}',\mathbf{u_2},\ldots,\mathbf{u_n})
$$
Thus we have
$$
\begin{split}
\det(\mathbf{u_1}&,\mathbf{u_2},\ldots,\mathbf{u_n})+\det(\mathbf{u_1}',\mathbf{u_2},\ldots,\mathbf{u_n})\\
&=\det(\mathbf{u_1}+\mathbf{u_1}',\mathbf{u_2},\ldots,\mathbf{u_n})
\end{split}
$$
as desired!

# Properties of the determinant

Besides the properties contained in Axioms 1 - 3 above it is easy to verify the following:

* $\det(\ldots,\mathbf{u},\ldots,\mathbf{v},\ldots)=-\det(\ldots,\mathbf{v},\ldots,\mathbf{u},\ldots)$

That is swapping two vectors (rows/columns) changes the sign.
* $\det(\mathbf{u_1},\ldots,\mathbf{u_n})=0 \iff \mathbf{u_1},\ldots,\mathbf{u_n}$ are not linearly independent.

For the first, consider
$$
\begin{split}
\det(\ldots,&\mathbf{u},\ldots,\mathbf{v},\ldots)
+\det(\ldots,\mathbf{v},\ldots,\mathbf{u},\ldots)\\
&=\det(\ldots,\mathbf{u},\ldots,\mathbf{v},\ldots) + \det(\ldots,\mathbf{v},\ldots,\mathbf{v},\ldots)\\
&\qquad\qquad+\det(\ldots,\mathbf{v},\ldots,\mathbf{u},\ldots)+
\det(\ldots,\mathbf{u},\ldots,\mathbf{u},\ldots)\\
&=\det(\ldots,\mathbf{u+v},\ldots,\mathbf{v},\ldots)
+\det(\ldots,\mathbf{v+v},\ldots,\mathbf{u},\ldots)\\
&=\det(\ldots,\mathbf{v+v},\ldots,\mathbf{u+v},\ldots)=0
\end{split}
$$
This just uses (1) of Axiom 2 and Axiom 1.

For the second, suppose WLOG that $\mathbf{u_1}$ is a linear combination of the rest of the vectors. Then $\mathbf{u_1}=\alpha_2\mathbf{u_2}+\cdots+\alpha_n\mathbf{u_n}$ and
$$
\begin{split}
\det(\mathbf{u_1},\mathbf{u_2},\ldots,\mathbf{u_n}) &=
\det\left(\sum_{i=2}^n\alpha_i\mathbf{u_i},\mathbf{u_2},\ldots,\mathbf{u_n}\right)\\
&=\sum_{i=2}^n\alpha_i\det(\mathbf{u_i},\ldots,\mathbf{u_i},\ldots)=0
\end{split}
$$

# The axioms are enough to compute the determinant

It turns out that the three axioms given suffice to show that $\det(\mathbf{u_1},\mathbf{u_2},\ldots,\mathbf{u_n})$ always yields a unique value and this is what we call the determinant.

Note that this yields immediately that
$$
\text{vol}(\mathbf{u_1},\ldots,\mathbf{u_n})=|\det(\mathbf{u_1},\ldots,\mathbf{u_n})|\tag{3}
$$
This is true since what we showed above was that any operation satisfying (3) must satisfy axioms 1 - 3. If satisfying those axioms is enough to yield a result, then (3) must hold.

Basically what one shows here is that the axioms lead to the usual expansion along columns. This is just a sort of tedious inductive proof, so I will just do the calculation for $\mathbb{R}^2$, then show how that leads to the usual expansion in $\mathbb{R}^3$, going from 2 to 3 indicates what must be done in the actual inductive step.

## Computing det(u,v)

In $\mathbb{R}^2$, the standard basis vectors are $\mathbf{e_1}=(1,0)$ and $\mathbf{e_2}=(0,1)$. An arbitrary vector $\mathbf{v}=(v_1,v_2)=v_1\mathbf{e_1}+v_2\mathbf{e_2}$. so using this notation, let's see that the axioms suffice to compute $\det(\mathbf{u},\mathbf{v})$.
$$
\begin{align*}
\det(\mathbf{u},\mathbf{v})&=\det(u_1\mathbf{e_1}+u_2\mathbf{e_2},v)\\
&=u_1\det(\mathbf{e_1},v)+u_2\det(\mathbf{e_2},v)\\
&=u_1\det(\mathbf{e_1},v_1\mathbf{e_1}+v_2\mathbf{e_2})+
u_2\det(\mathbf{e_1},v_1\mathbf{e_1}+v_2\mathbf{e_2})\\
&=u_1\bigl(v_1\det(\mathbf{e_1},\mathbf{e_1})+v_2\det(\mathbf{e_1},\mathbf{e_2})\bigr)+
u_2\bigl(v_1\det(\mathbf{e_2},\mathbf{e_1})+v_2\det(\mathbf{e_2},\mathbf{e_2})\bigr)\\
&=u_1v_1\det(\mathbf{e_1},\mathbf{e_1})+u_1v_2\det(\mathbf{e_1},\mathbf{e_2})+
u_2v_1\det(\mathbf{e_2},\mathbf{e_1})+u_2v_2\det(\mathbf{e_2},\mathbf{e_2})\\
&=u_1v_1\cdot 0+u_1v_2\cdot 1 +u_2v_1\cdot(-1)+u_2v_2\cdot 0\\
&=u_1v_2-u_2v_1
\end{align*}
$$
This is the usual value of the determinant:
$$
\det(\mathbf{u},\mathbf{v})=\det\begin{bmatrix}u_1&v_1\\u_2&v_2\end{bmatrix}=u_1v_2-u_2v_1
$$

## Computing det(u,v,w)

As above we use the notation $\mathbf{u}=u_1\mathbf{e_1}+u_2\mathbf{e_2}+u_3\mathbf{e_3}$ so
$$
\begin{align*}
\det(\mathbf{u},\mathbf{v},\mathbf{w})&=
\det\left(\sum_{i=1}^3u_i\mathbf{e_i},\mathbf{v},\mathbf{w}\right)\\
&=\sum_{i=1}^n u_i\det(\mathbf{e_i},\mathbf{v},\mathbf{w})\\
\end{align*}
$$
So we just need to see that $\det(\mathbf{e_i},\mathbf{v},\mathbf{w})$ corresponds to the (i,1)-minor (essentially we are expanding along the first column). This is easy, I'll do $i=2$, just to see where the $-1$ comes from
$$
\begin{align*}
\det(\mathbf{e_2},\mathbf{v},\mathbf{w})&=
\det(\mathbf{e_2},v_1\mathbf{e_1}+v_2\mathbf e_2+v_3\mathbf{e_3},w_1\mathbf{e_1}+w_2\mathbf e_2+w_3\mathbf{e_3})\\
&=\det(\mathbf{e_2},(v_1\mathbf{e_1}+v_3\mathbf{e_3})+v_2\mathbf e_2,(w_1\mathbf{e_1}+w_3\mathbf{e_3})+w_2\mathbf e_2)\\
&=\det(\mathbf{e_2},v_1\mathbf{e_1}+v_3\mathbf{e_3},(w_1\mathbf{e_1}+w_3\mathbf{e_3})+w_2\mathbf e_2)
+\det(\mathbf{e_2},v_2\mathbf e_2,(w_1\mathbf{e_1}+w_3\mathbf{e_3})+w_2\mathbf e_2)\\
&=\det(\mathbf{e_2},v_1\mathbf{e_1}+v_3\mathbf{e_3},(w_1\mathbf{e_1}+w_3\mathbf{e_3})+w_2\mathbf e_2)\\
&=\det(\mathbf{e_2},v_1\mathbf{e_1}+v_3\mathbf{e_3},
w_1\mathbf{e_1}+w_3\mathbf{e_3})+\det(\mathbf{e_2},v_1\mathbf{e_1}+v_3\mathbf{e_3},w_2\mathbf e_2)\\
&=\det(\mathbf{e_2},v_1\mathbf{e_1}+v_3\mathbf{e_3},w_1\mathbf{e_1}+w_3\mathbf{e_3})\\
&=-\det(v_1\mathbf{e_1}+v_3\mathbf{e_3},\mathbf{e_2},w_1\mathbf{e_1}+w_3\mathbf{e_3})\\
&=-(v_1w_3-v_3w_1)\\
&=(-1)^{2+1}\det(M_{2,1})
\end{align*}
$$

## Computing det(u₁,...,uₙ)

As above $\mathbf{u_i}=\sum_{j=1}^n {u_{ij}}\mathbf{e_j}$ and so
\begin{align}
\det(\mathbf{u_1},\mathbf{u_2},\ldots,\mathbf{u_i},\ldots,\mathbf{u_n})&=
\det\left(\mathbf{u_1},\mathbf{u_2},\ldots,\sum_{j=1}^n {u_{ij}}\mathbf{e_j},\ldots,\mathbf{u_n}\right)\\
&=\sum_{i=1}^n u_{ij}\det(\mathbf{u_1},\mathbf{u_2},\ldots,\mathbf{e_j},\ldots,\mathbf{u_n})
\end{align}

[^std]: Recall that in this class we use $\bf e_i^n$ to be the $i$^th^ standard basis element in $\mathbb R^n$. The $n$ is often determined from context. So $\bf e_1=\bf i=\Bigl[\begin{smallmatrix}1\\0\end{smallmatrix}\Bigr]$ and $\bf e_2=\bf j=\Bigl[\begin{smallmatrix}0\\1\end{smallmatrix}\Bigr]$.