# Randomness
Bob has two cups that are idential in shape. However, since Bob suffers from red-green color blindness, Bob cannot tell whether the two cups are the same
color or are red and green. Alice claims that these two cups have different colors.
Please design a proof strategy for Bob to examine whether Alice’s claim is true or not without relying on others or any special equipment. (NTU CNS 2020 Spring)
#### Reference
- 旭君全餐
## Case study
1. Q: UUID can be trancated or not
https://gitlab.com/DYSK_Labs/data-team/ai-services/annotation-logger/-/blob/93d64076cf0e02d8b0e35a2430b7f9bcee8af3b8/annotation_logger/base_workflows.py#L76
https://gitlab.com/DYSK_Labs/data-team/ai-services/annotation-logger/-/merge_requests/20
```python=
contour_uuid = slide_contour['uuid'].split('-')[0],
```
2. Q: What is the problem if I want to record multiple XXX_done tags for each slide.
https://gitlab.com/DYSK_Labs/data-team/ai-services/annotation-logger/-/merge_requests/29
```python=
contour_uuid = hash_string_and_generate_pseudo_uuid(slide_contours['slide_name'])
```
3. Q. Does this function promise enough randomness
```python=
def hash_string_and_generate_pseudo_uuid(s):
hash_object = hashlib.sha256(s.encode('utf-8'))
hex_dig = hash_object.hexdigest()
return f'{hex_dig[:8]}-{hex_dig[8:12]}-{hex_dig[12:16]}-{hex_dig[16:20]}-{hex_dig[20:32]}'
```
## UUID (Universally Unique Identifier)
- Format:
- A sequence of digits equal to 128 bits (32*8).
- Big-endian
- The ID is in hexadecimal digits
- `XXXXXXXX-XXXX-XXXX-XXXX-XXXXXXXXXXXX`
- Is UUID promise an *negligible* collison probability with a space of $2^{128}$?
- Is a truncated UUID with a lenth $L$, where $L \leq 128$ promise an space of $2^{L}$?
- NO!
- `xxxxxxxx-xxxx-Mxxx-Nxxx-xxxxxxxxxxxx`
- M: version
- N: variance
### UUID V1 (date-time and MAC address)
```python!
import uuid
# uuid.uuid1(node=None, clock_seq=None)
# Generate a UUID from a host ID, sequence number, and the current time. If node is not given, getnode() is used to obtain the hardware address. If clock_seq is given, it is used as the sequence number; otherwise a random 14-bit sequence number is chosen.
>>> uuid.uuid1()
UUID('16867e3e-fa17-11ed-a54c-bb709f202970')
>>> uuid.uuid1()
UUID('1862cb5e-fa17-11ed-a54c-bb709f202970')
>>> uuid.uuid1()
UUID('197ec998-fa17-11ed-a54c-bb709f202970')
>>> uuid.uuid1()
UUID('197ec999-fa17-11ed-a54c-bb709f202970')
>>> uuid.uuid1()
UUID('1dac3758-fa17-11ed-a54c-bb709f202970')
```

- 60-bit 的時間戳和節點(生成UUID的電腦)的48-bit MAC位址而生成的
- 基於網卡MAC位址的「版本1」和「版本2」UUID 的唯一性還取決於網卡製造商正確地為其卡分配唯一的MAC位址,這與其他製造過程一樣容易出錯
- 此外,某些作業系統允許終端使用者自訂MAC位址,例如OpenWRT
- 使用節點的網路MAC位址作為節點ID,代表可以透過版本1的UUID逆向找到建立它的電腦。
- Melissa
- Security issue
- 可以從生成值的前 3 個欄位確定大致時間
- 連續的 UUID 值之間有很多重複的欄位
- 第一個欄位,"time-low",每 429 秒翻轉一次
- MySQL UUID 函數產生 V1 版本值
### UUID V2 (date-time and MAC address, DCE security version)
- 時鐘序列的最低有效8 bits 被「本地域(local domain)」號替換
- 時間戳的最低有效32 bits 由在指定本地域內有意義的整數識別碼替換
- 每7分鐘時鐘周期內,每個節點、域或識別碼只能生成64個唯一的UUID
- 版本2可能不適合用於以節點、域或識別碼在約7秒以上1次的速率下生成 UUID 的情況
### UUID V3
```python!
import uuid
# uuid.uuid3(namespace, name)
# Generate a UUID based on the MD5 hash of a namespace identifier (which is a UUID) and a name (which is a string).
>>> uuid.uuid3(uuid.NAMESPACE_URL, 'rnd_string1')
UUID('50ddfd70-1d92-3aac-bbf5-c0a78a186b8a')
>>> uuid.uuid3(uuid.NAMESPACE_URL, 'rnd_string2')
UUID('80224320-967f-3a81-99b1-9a452d5efaf7')
```
- MD5
- Generate
- The namespace identifier is itself a UUID. The specification provides UUIDs to represent the namespaces for URLs, fully qualified domain names, object identifiers, and X.500 distinguished names; but any desired UUID may be used as a namespace designator.
- To determine the version-3 UUID corresponding to a given namespace and name, the UUID of the namespace is transformed to a string of bytes, concatenated with the input name, then hashed with MD5, yielding 128 bits.
- Then 6 or 7 bits are replaced by fixed values, the 4-bit version (e.g. 00112 for version 3), and the 2- or 3-bit UUID "variant" (e.g. 102 indicating a RFC 4122 UUIDs, or 1102 indicating a legacy Microsoft GUID). Since 6 or 7 bits are thus predetermined, only 121 or 122 bits contribute to the uniqueness of the UUID.
- Security issue of MD5 (-> 128 bits)
- algorithm
- $F(X,Y,Z)=(X\land Y)\lor (\neg X\land Y)$
- $G(X,Y,Z)=(X\land Z)\lor (Y\land \neg Z)$
- $H(X,Y,Z)=X \oplus Y \oplus Z$
- $I(X,Y,Z)=Y\oplus (X \lor \neg Z)$
- [Fast Collision Attack on MD5](https://www.win.tue.nl/hashclash/fastcoll.pdf)
- complexity: $2^{32.3}$
### UUID V5
- Similiar to V3
- SHA1
### UUID V4
- Random
- Space: $2^{122}$
- 一些偽亂數發生器缺少必要的熵來產生足夠的偽亂數。
- WinAPI GUID 生成器已被證明可生成遵循可預測模式的 UUID。
- RFC 4122 建議「在各種主機上生成 UUID 的分散式應用程式必須願意依賴所有主機上的亂數源。如果這不可行,則應使用名稱空間變體。」
```python
def uuid4():
"""Generate a random UUID."""
return UUID(bytes=os.urandom(16), version=4)
```
- Python: dependent on `os.urandom(16)`
```c!
// https://github.com/python/cpython/blob/c43785192c97698a0217a680b30baae22106ed3e/Python/bootstrap_hash.c#L117
static int
py_getrandom(void *buffer, Py_ssize_t size, int blocking, int raise)
{
/* Is getrandom() supported by the running kernel? Set to 0 if getrandom()
failed with ENOSYS or EPERM. Need Linux kernel 3.17 or newer, or Solaris
11.3 or newer */
static int getrandom_works = 1;
int flags;
char *dest;
long n;
if (!getrandom_works) {
return 0;
}
flags = blocking ? 0 : GRND_NONBLOCK;
dest = buffer;
while (0 < size) {
#if defined(__sun) && defined(__SVR4)
/* Issue #26735: On Solaris, getrandom() is limited to returning up
to 1024 bytes. Call it multiple times if more bytes are
requested. */
n = Py_MIN(size, 1024);
#else
n = Py_MIN(size, LONG_MAX);
#endif
errno = 0;
#ifdef HAVE_GETRANDOM
if (raise) {
Py_BEGIN_ALLOW_THREADS
n = getrandom(dest, n, flags);
Py_END_ALLOW_THREADS
}
else {
n = getrandom(dest, n, flags);
}
#else
/* On Linux, use the syscall() function because the GNU libc doesn't
expose the Linux getrandom() syscall yet. See:
https://sourceware.org/bugzilla/show_bug.cgi?id=17252 */
if (raise) {
Py_BEGIN_ALLOW_THREADS
n = syscall(SYS_getrandom, dest, n, flags);
Py_END_ALLOW_THREADS
}
else {
n = syscall(SYS_getrandom, dest, n, flags);
}
# ifdef _Py_MEMORY_SANITIZER
if (n > 0) {
__msan_unpoison(dest, n);
}
# endif
#endif
if (n < 0) {
/* ENOSYS: the syscall is not supported by the kernel.
EPERM: the syscall is blocked by a security policy (ex: SECCOMP)
or something else. */
if (errno == ENOSYS || errno == EPERM) {
getrandom_works = 0;
return 0;
}
/* getrandom(GRND_NONBLOCK) fails with EAGAIN if the system urandom
is not initialized yet. For _PyRandom_Init(), we ignore the
error and fall back on reading /dev/urandom which never blocks,
even if the system urandom is not initialized yet:
see the PEP 524. */
if (errno == EAGAIN && !raise && !blocking) {
return 0;
}
if (errno == EINTR) {
if (raise) {
if (PyErr_CheckSignals()) {
return -1;
}
}
/* retry getrandom() if it was interrupted by a signal */
continue;
}
if (raise) {
PyErr_SetFromErrno(PyExc_OSError);
}
return -1;
}
dest += n;
size -= n;
}
return 1;
}
```
- getrandom
```c
#include <sys/random.h>
ssize_t getrandom(void *buf, size_t buflen, unsigned int flags);
```
- Get the entropy in `/dev/random`
- Linux核心中的是第一個以背景噪聲產生真正的亂數產生的實現,它允許程式存取來自裝置驅動程式或其它來源的背景噪聲
- [For more details](https://szlin.me/2016/10/05/%E5%88%9D%E6%8E%A2-linux-kernel-%E4%BA%82%E6%95%B8%E7%94%A2%E7%94%9F%E5%99%A8-random-generator/)
## Pseudo random number generator (PRNG)
$\{0,1\}^{N} \rightarrow \{0,1\}^{*}$
### LFSR (Linear feedback shift register)


- space: $2^N$
- Can be used to generate a key for XOR cipher?
- Known Plaintext Attack
- 2N bits to break it
- Berlekamp Massey Algorithm
- Use linear recurrence to break it
### Trivium

- Correlation Attack
- [Example](https://blog.bi0s.in/2020/08/02/Crypto/LFSR/InCTFi-20-FaultyLFSR/)
- $2^{32 \times 3}$ to $3\times 2^{32}$
- [Fast Correlation Attack](https://projects.cs.uct.ac.za/honsproj/cgi-bin/view/2011/desai.zip/crypto_desai/index.html)
### Mersenne twister (MT19937)
- 整個算法主要分為三個階段:
- 第一階段:獲得基礎的梅森旋轉鏈
- 第二階段:對於旋轉鏈進行旋轉算法 (LFSR)
- 第三階段:對於旋轉算法所得的結果進行處理
- Python uses the Mersenne Twister as the core generator. It produces 53-bit precision floats and has a period of 2**19937-1
- Seed: 32bits
- Predict output of Mersenne Twister after seeing 624 values: [tool](https://github.com/kmyk/mersenne-twister-predictor)
- [Trust Wallet security issue](https://github.com/trustwallet/wallet-core/pull/2240)
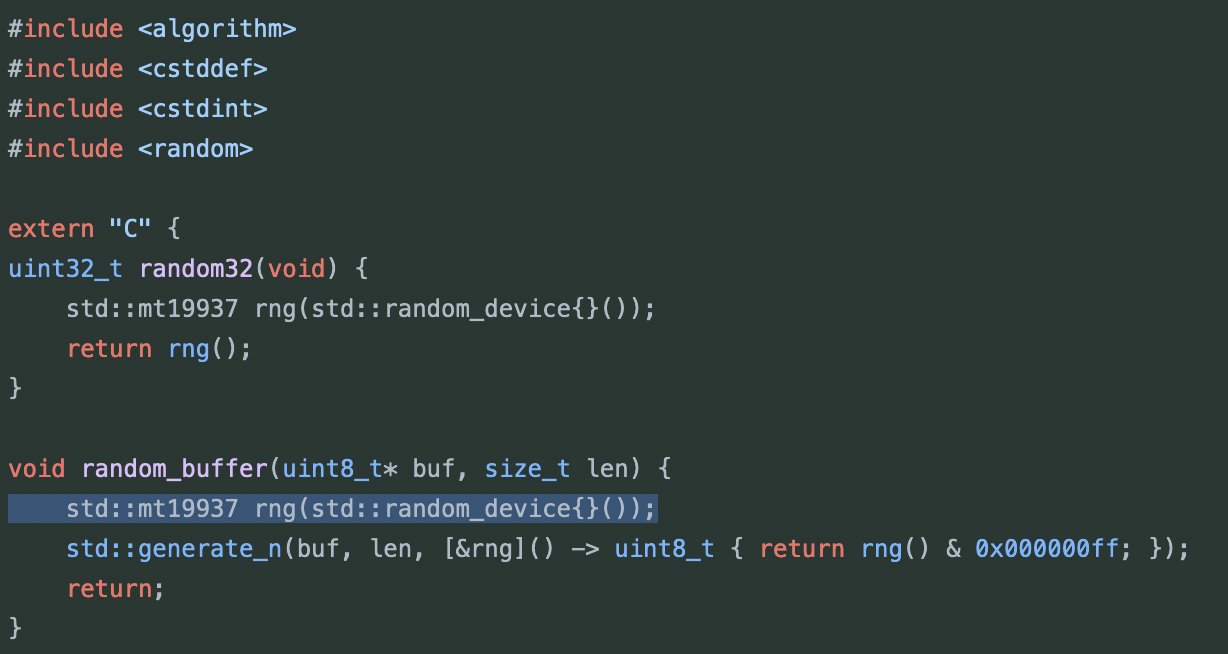
- Trust Wallet犯的錯誤是,他們使用了std::random_device來生成seed。在wasm環境下,由於sandbox特性,它根本不具備隨機性。
- How does Python seed random?
```python!=
# 3.3
class Random(_random.Random):
"""Random number generator base class used by bound module functions.
Used to instantiate instances of Random to get generators that don't
share state.
Class Random can also be subclassed if you want to use a different basic
generator of your own devising: in that case, override the following
methods: random(), seed(), getstate(), and setstate().
Optionally, implement a getrandbits() method so that randrange()
can cover arbitrarily large ranges.
"""
VERSION = 3 # used by getstate/setstate
def __init__(self, x=None):
"""Initialize an instance.
Optional argument x controls seeding, as for Random.seed().
"""
self.seed(x)
self.gauss_next = None
def seed(self, a=None, version=2):
"""Initialize internal state from hashable object.
None or no argument seeds from current time or from an operating
system specific randomness source if available.
For version 2 (the default), all of the bits are used if *a *is a str,
bytes, or bytearray. For version 1, the hash() of *a* is used instead.
If *a* is an int, all bits are used.
"""
if a is None:
try:
a = int.from_bytes(_urandom(32), 'big')
except NotImplementedError:
import time
a = int(time.time() * 256) # use fractional seconds
if version == 2:
if isinstance(a, (str, bytes, bytearray)):
if isinstance(a, str):
a = a.encode("utf8")
a += _sha512(a).digest()
a = int.from_bytes(a, 'big')
super().seed(a)
self.gauss_next = None
```
```python!=
# 3.12
class Random(_random.Random):
"""Random number generator base class used by bound module functions.
Used to instantiate instances of Random to get generators that don't
share state.
Class Random can also be subclassed if you want to use a different basic
generator of your own devising: in that case, override the following
methods: random(), seed(), getstate(), and setstate().
Optionally, implement a getrandbits() method so that randrange()
can cover arbitrarily large ranges.
"""
VERSION = 3 # used by getstate/setstate
def __init__(self, x=None):
"""Initialize an instance.
Optional argument x controls seeding, as for Random.seed().
"""
self.seed(x)
self.gauss_next = None
def seed(self, a=None, version=2):
"""Initialize internal state from a seed.
The only supported seed types are None, int, float,
str, bytes, and bytearray.
None or no argument seeds from current time or from an operating
system specific randomness source if available.
If *a* is an int, all bits are used.
For version 2 (the default), all of the bits are used if *a* is a str,
bytes, or bytearray. For version 1 (provided for reproducing random
sequences from older versions of Python), the algorithm for str and
bytes generates a narrower range of seeds.
"""
if version == 1 and isinstance(a, (str, bytes)):
a = a.decode('latin-1') if isinstance(a, bytes) else a
x = ord(a[0]) << 7 if a else 0
for c in map(ord, a):
x = ((1000003 * x) ^ c) & 0xFFFFFFFFFFFFFFFF
x ^= len(a)
a = -2 if x == -1 else x
elif version == 2 and isinstance(a, (str, bytes, bytearray)):
if isinstance(a, str):
a = a.encode()
a = int.from_bytes(a + _sha512(a).digest())
elif not isinstance(a, (type(None), int, float, str, bytes, bytearray)):
raise TypeError('The only supported seed types are: None,\n'
'int, float, str, bytes, and bytearray.')
super().seed(a)
self.gauss_next = None
```
## Cryptographic hash functions
- General one
- $\mathcal{H}: \mathcal{M}\rightarrow \mathcal{T}$
- $\{0,1\}^{*}\rightarrow \{0,1\}^{t}$
- Collisions are inevitable
- $|\mathcal{M}| >> |\mathcal{T}|$
- Collisions are easy to find
- Cryptographic one: Collisions are hard to find
- One-wayness (preimage resistance)
- Given $y$, hard to find $x$ s.t. $y = H(x)$
- 有意義的時間內難以回推
- Weak collision resistance (2nd-preimage resistance)
- Given $x$, hard to find $x^\prime ≠ x$ s.t. $H(x^\prime)=H(x)$
- 對於一個x,很難找到collison
- Strong collision resistance (collision resistance)
- Hard to find $x$ and $x^\prime$ s.t. $x^\prime ≠ x$ and $H(x^\prime)=H(x)$
- 連一組collision都很難找到
- Attack complexity
- One-wayness
- find $x$ after $2^{n - 1}$ trials
- Weak collision resistance
- find $x^\prime$ after $2^{n - 1}$ trials
- Strong collision resistance
- find a collision after $2^{n/2}$ trials
- Birthday paradox
- Properties
- Strong collision resistance $\Rightarrow$ Weak collision resistance $\Rightarrow$ One-wayness
- Well-known algorithms
- MD5, SHA1, SHA256, SHA3, ...
- Merkle-Damgård construction

- Used in MD5, SHA-1, SHA-2
- Suffer from Length extension attacks
- 攻擊者可以利用H(訊息1)和訊息1的長度,不知道訊息1內容的情形下,將攻擊者控制的訊息2計算出H(訊息1 ‖ 訊息2)。
- **不能作為MAC(Message Authentication Codes)**
- Sponge construction

- SHA3
- Free from Length extension attacks
- [SHA family](https://zh.wikipedia.org/zh-tw/SHA%E5%AE%B6%E6%97%8F)
- Collision
- Rainbow Table: [ophcrack](https://ophcrack.sourceforge.io/)
- Broken hash functions
- MD5
- [SHA1](https://shattered.io/)
