# Pairings and applications <!-- Put the link to this slide here so people can follow --> slide: https://hackmd.io/@jVkDzwsSRbCqx36bM2T_dA/rk_XGdnVT --- ## Prime finite field * A prime field consists of numbers $0,1,2,...,p-1$ where $p$ is prime * Math operations are defined as follows: * $a+b: (a+b)\pmod{p}$ * $a\cdot b: (a\cdot b)\pmod{p}$ * $a-b:(a-b)\pmod{p}$ * $a/b:(a\cdot b^{p-2})\pmod{p}$ * Notation for such field is $F_p$ --- ### Why primes?  Multiplication table $\pmod{12}$ --- ### Why primes?  Multiplication table $\pmod{7}$ --- ### Discrete log problem * Given $A=g^a\pmod{p}$. * Recover $a$ only knowing $A$ and $g$ --- ## Diffie-Hellman key exchange How to generate a shared secret key? Fix prime $p$ and $g \in F_p$  --- ### Computational Diffie-Hellman (CDH) problem  Eavesdropper sees: $p$, $g$, $A=g^a \pmod{p}$, and $B=g^b\pmod{p}$ **CDH**: given $(g,g^a, g^b)$ **compute** $g^{ab}\pmod{p}$ In DH key exchange CDH problem is hard --- ### Decisional Diffie-Hellman (DDH) problem * Given $(g,g^a, g^b, g^c)$ * **check if** $g^c\pmod{p}=g^{ab}\pmod{p}$ * DDH is considered to be hard problem --- ## Elliptic curves * Elliptic curve is a set of points solving the following equation: $E$: $y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6$ * In practice majority of applications use *short Weierstrass equation*: $E$: $y^2=x^3+ax+b$ --- ## Elliptic curves  --- ### Elliptic curve additions <!-- 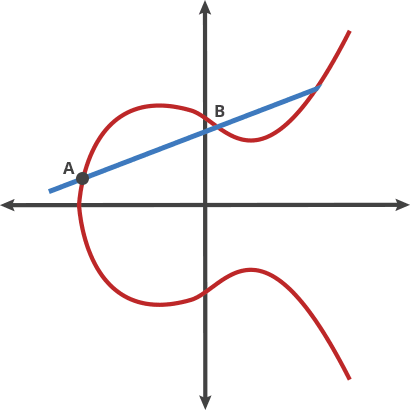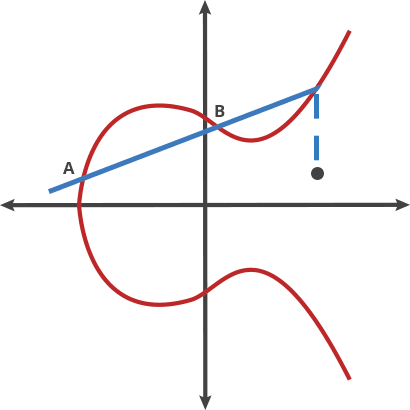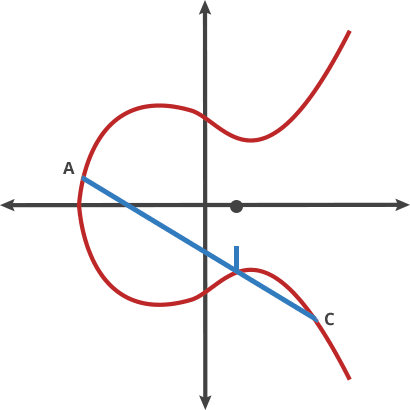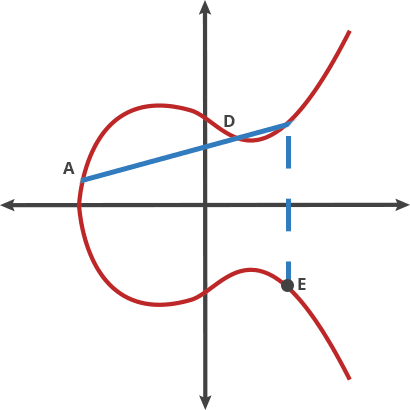 -->  --- ### What if P == Q  --- ### Elliptic curve additions  --- * For our purposes we will always use elliptic curve defined over a set of integers belonging to finite field $F_p$: * $y^2=x^3+ax+b\pmod{p}$ <!--  -->  --- ### 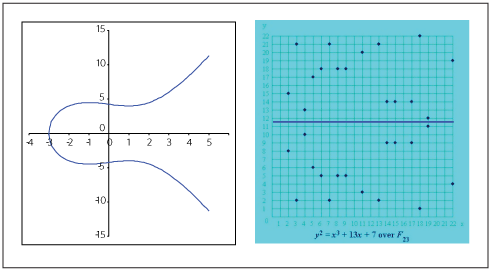Hasse-Weil bound For all primes $p$ and $a,b$: number of points on $y^2=x^3+ax+b \pmod{p}$ is "about" p --- ### Elliptic curve scalar multiplication * Given field element $u\in F_p$ and elliptic curve $P \in E$. * Scalar multiplication is an addition of point $P$ to itself $u$ times: * $uP=\overbrace{P+P+...+P}^{u\text{ times}}$ --- ### Elliptic curve group $\mathbb{G}$ defines a group over a set of elliptic curve as follows: * A chosen $P\in E$ is called a generator * element $x\in F_P$ is represented in group $\mathbb{G}$ as $xP$ * Notation: * $[x]=xP$ * $\mathbb{G}=\langle P \rangle$ --- ### Elliptic curve discrete log problem Given $P\in E$ and $A=aP$ where $a\in F_p$ Recover $a$ only knowing $P$ and $A$ --- ### Elliptic curve Diffie-Hellman (ECDH) key exchange * Fix prime $p$, * curve $y^2=x^3+ax+b\pmod{p}$ * and point **P** on curve  --- ### Elliptic curve CDH problem * **CDH**: given (P, uP, vP) **compute** (uv)P * In ECDH key exchange CDH problem is hard  --- ### Elliptic curve DDH problem * Given (P,uP, vP, hP) * **check if** hP=uvP * In ECDH key exchange DDH problem is hard  --- ### Elliptic curve signatures TODO --- ## Bilinear Pairings * Consider groups $\mathbb{G}_1$,$\mathbb{G}_2$, and $\mathbb{G}_T$ * We call operator $e=\mathbb{G}_1 \cross \mathbb{G}_2 \rightarrow \mathbb{G}_T$ bilinear pairing if it satisfies the following properties: * $\forall P,S \in \mathbb{G}_1$ and $\forall Q,R\in \mathbb{G}_2$,: $e(P,Q+R) = E(P,Q)\cdot E(P,R)$ $e(P+S,Q) = E(P,Q)\cdot E(S,Q)$ * This implies $e(aP,bR)=e(P,R)^{ab}$ * sometimes $\mathbb{G}_1$ and $\mathbb{G}_2$ are the same --- ### Bilinear pairing over a simple integers * If $P,Q,R,S$ were simple integers instead of elliptic curve points, then making pairing is easy * We can do $e(x,y)=2^{xy}$. Then we can see: * $e(3,4+5)=2^{3\cdot 9} = 2^{27}$ * $e(3,4)\cdot e(3,5)=2^{3\cdot 4} \cdot 2^{3\cdot 5}=2^{12}\cdot 2^{15}=2^{27}$ * However, such simple pairings are not suitable for us because these integers are too easy to divide or compute logarithms --- ### Discrete log problem using bilinear pairings * Consider $Q=aP$ where $a$ is unknown and $Q$ and $P$ have the following relation: * $e(P,Q)=e(P,aP)=e(P,P)^a$ * DLT problem is to compute $a$ from $e(P,Q)$ * Discrete log problem is still hard --- ### DDH in bilinear pairings (BDDH) * Given $G,P,Q,R\in \mathbb{G}_1$ where * $P=pG$, $Q=qG$, $R=rG$ * Checking whether or not $p\cdot q = r$ is **easy** by knowing $G,P,Q,R$ by checking pairing equation: * $e(P,Q)=e(R,G)$ * $e(G,G)^{pq}=e(G,G)^{r}$ --- ### CDH in biliniear pairings (BCDH) * Given $G,P=pG,Q=qG$, compute $e(G,G)^{pq}$ * CDH problem is still hard --- ## Pairing protocols --- ### Three party key exchange * Let's extend ECDH key exchange to 3 party (Alice, Bob and Chris) * corresponding private keys are $a,b,c\in F_p$ * Parties use $\mathbb{G}=\langle P \rangle$ * To calculate shared secret $K=abcP$ at least two round of communications are required  --- ### Three-party one-round key exchange * In parallel: a. $Alice\rightarrow Bob,Charlie: aP$ b. $Bob\rightarrow Alice,Charlie: bP$ c. $Chris\rightarrow Bob,Charlie: cP$  --- ### Three-party one-round key exchange * In parallel * Alice computes $e(bP,cP)^a=e(P,P)^{abc}$ * Bob computes $e(aP,cP)^b=e(P,P)^{abc}$ * Chris computes $e(aP,bP)^c=e(P,P)^{abc}$ * $e(P,P)^{abc} \in \mathbb{G}_2$ is a shared key --- ### Multi-party key exchange * To perform Multi-party one-round key-exchange we need the existence of pairing with arbitrary number of arguments * Otherwise is standard 2-argument pairing is used, we will need $log(n)$ rounds where $n$ is number of participants --- ### BLS Signatures (short signatures) * Boneh, Lynn and Shacham proposed signature scheme in which signatures are comprised of a single group element * Given: * $\mathbb{G}_1=\langle P \rangle$ * pairing $e=\mathbb{G}_1 \cross \mathbb{G}_1 \rightarrow \mathbb{G}_T$ * Alice's private key $a\in F_p$ * Alice's public key is $A=aP$ * Message $m\in \{0,1\}^*$ * We need Alice to sign message $m$ --- ### BLS Signatures (short signatures) * Alice calculates hash $M=H(m)$ * Alice's signature on a message $m$ is a single group element $S=aM$ * Anyone posessing Alice's public key can verify $S$ by computing: * $e(P,S)=e(A,M)$, because: * $e(P,aM)=e(aP,M)$ * $e(P,M)^a=e(P,M)^a$ * This is exactly the instance of Bilinear DDH problem --- ### BLS signature aggregation * Assume now we have $n$ parties $A_1, A_2, ..., A_n$ who wish to sign the same message * Aggregated signature is $S_{aggr}=\sum_{i=1}^{n} S_i$ * Aggregated pubkey is $A_{aggr}=\sum_{i=1}^{n}A_i$ * Verification is: * $e(P,S_{aggr})=e(A_{aggr},M)$, because: * $e(P,\sum S_i)=e(\sum A_i,M)$ * $e(P,\sum a_iM)=e(\sum a_iP,M)$ * $e(P,M)^{\sum a_i}=e(P,M)^{\sum a_i}$ --- ## Resources --- * Good short intro: [link](https://courses.csail.mit.edu/6.897/spring04/L25.pdf) * Good longer intro: [link](https://www.math.uwaterloo.ca/~ajmeneze/publications/pairings.pdf) * Good even longer intro: [link](https://static1.squarespace.com/static/5fdbb09f31d71c1227082339/t/5ff394720493bd28278889c6/1609798774687/PairingsForBeginners.pdf) * Good Vitalik's article: [link](https://www.vitalik.ca/general/2017/01/14/exploring_ecp.html) * Good summary of all above: [link](https://hackmd.io/@benjaminion/bls12-381#Roots-of-unity) * Vitalik's presentation on BLS aggregation: [link](https://www.youtube.com/watch?v=DpV0Hh9YajU&t=510s) * Dan Boneh's presentation about DH and elliptic curves: [link](https://www.youtube.com/watch?v=4M8_Oo7lpiA&t=3368s) * 20-hours youtube course on pairings: [link](https://www.youtube.com/playlist?list=PL8Vt-7cSFnw2V2Wpf4MpwtSJvLvZo1ADB)