# ignacio (jsign) - Update 14

In these last two weeks, I worked in two interestng tasks.

## Explore serializing vector commitments as uncompressed elliptic curve points

The title might sounds a bit cryptic, but it all started by noticing this in our latest benchmark:

What that means is that we're spending 20% of CPU time running `computeY(...)`. This function is called as part of `ParseNode(...)` which reads saved information in the Ethereum EL client, and deserialize that into a Verkle Node node.

The way we were serializing Verkle Node nodes, which contains elliptic curve points for vector commitments, was serializing the _compressed_ elliptic curve point. An elliptic curve point in affine form is composed of two coordinates `X` and `Y`.

The _compressed_ serialization means that we only save the `X` coordinate. Whenever we deserialize the point, we can recover the `Y` coordinate by re-calculating the value using the elliptic curve formulas. Unfortunately, this formula involves a bunch of addition, multiplication and inverse operation which are costly.

My idea was considering persisting points in uncompressed form, so both saving `X` and `Y` which would avoid CPU calculations when deserializing the points. This has the tradeoff of doubling the sizeo of the serialized points, but maybe that's a good tradeoff if shreds 15-20% of CPU.

I've shared this idea with Guillaume and Kevaundray which validated it was worth trying it.

I implemented the changes to explore this idea in the following PRs:
- https://github.com/gballet/go-verkle/pull/323
- https://github.com/crate-crypto/go-ipa/pull/33

We have run this change in our most complete benchmark, but we still have some extra work to do to accomodate the `go-ethereum` part of the benchmark to get the results. We'll probably do that next, and we'll see what is our conclusion!

## I compared our current `CommitToPoly(...)` implementations vs three other potential ideas

At the crux of Verkle Tries commitments, is a multiscalar multiplication. This means a calculation like: `f1 * G1 + f2 * G2 + ...` where `f` are field elements and `G` are curve points.

We use an optimized version of an algorithm to do this calculation, which leverages the fact that in Verkle Tries case the points `G1`, `G2`, etc are fixed.

Despite we haven't explored until now that there might be something to gain on this front, I thought about the possibility that might be the case.

This ended up in a rabbit hole where I thought about other three potential ways or twists to do this calculation, which leaded to interesting results to be considered.

Leaving here some plot that I did as part of this work, you can get a sense on how I try to compare our current implementation against these other ideas to see how they scale on a particular dimension (lower is better):
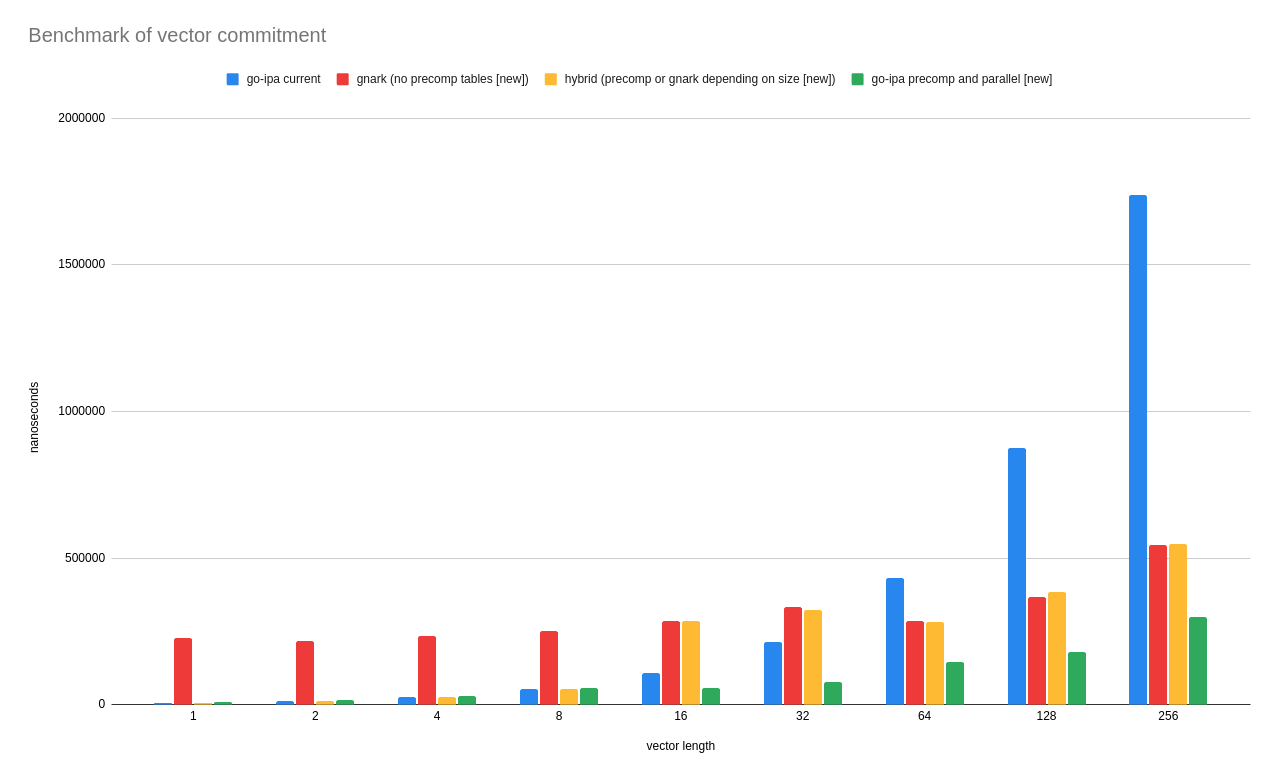
[Right-click and open in a new tab to see it better]

Since this was a somewhat complex exploration, [I summarized my finding in the following document that I recommend reading](https://hackmd.io/@jsign/committopoly-comparison).

Related PR: https://github.com/crate-crypto/go-ipa/pull/35