--- ###### tags: `2021 師大附中資訊科暑期培訓` --- # 二分搜尋法 2021 師大附中資訊科暑期培訓 joylintp --- ## 猜數字 有一整數 $n\ (1 \leq n \leq 10^6)$， 每次你可以猜一個介於 $1$ 和 $10^6$ 間的整數， 若 $n$ 大於或等於你猜的數字，你會收到 ``>=`` 否則，你會收到 ``<`` 你必須在 $25$ 次內猜到答案 [Gym - 101021 - 1](https://codeforces.com/gym/101021/problem/1) ---- 逐個數字猜 → 至多需要猜 $10^6$ 個數字 → Wrong Answer ---- 每次從已知的可能範圍切一半猜 → 至多需要猜 $\lceil log_2(10^6)\rceil = 20$ 次 → Accepted ---- ```cpp= #include<bits/stdc++.h> using namespace std; signed main() { int l = 1, r = 1000001; // l <= N < r string s; while (l != r - 1) { int Q = l + (r - l) / 2; cout << Q << endl; cin >> s; if (s == "<") r = Q; // N < Q else l = Q; // Q <= N } cout << "! " << l << endl; return 0; } ``` --- ## 二分搜陣列內容 有一長度為 $n\ (1 \leq n \leq 10^5)$ 的遞增正整數陣列 $A$， $q$ 次詢問某整數 $k$ 在陣列中的位置，或 $k$ 不存在於陣列中 ---- 一項一項找 → $O(n)$ ---- 設 $A_x = k$ 若 $k < A_P$，則 $x < P$（$k$ 會在第 $P$ 個位置的左邊） 若 $k \ge A_P$，則 $x \ge P$（$k$ 會在第 $P$ 個位置的右邊） → $O(log(n))$ ---- ```cpp= #include<bits/stdc++.h> using namespace std; signed main() { ios_base::sync_with_stdio(false); cin.tie(0); int n, q; cin >> n >> q; vector<int> A(n + 1); for (int i = 1; i <= n; i++) cin >> A[i]; int k; while (Q--) { cin >> k; int l = 0, r = n + 1; // l <= x < r while (l != r - 1) { int P = l + (r - l) / 2; if (k < A[P]) r = P; // x < P else l = P; // P <= x } if (A[l] == k) cout << l << '\n'; else cout << "-1\n"; } return 0; } ``` ---- ### lower_bound ```cpp= vector<int> v = {1, 2, 3, 5, 6}; cout << lower_bound(v.begin(), v.end(), 2) - v.begin() << '\n'; // -> 1 cout << lower_bound(v.begin(), v.end(), 0) - v.begin() << '\n'; // -> 0 cout << lower_bound(v.begin(), v.end(), 4) - v.begin() << '\n'; // -> 3 cout << lower_bound(v.begin(), v.end(), 7) - v.begin() << '\n'; // -> 5 // lower_bound回傳第一個「大於或等於」x的元素的iterator ``` ---- ```cpp= #include<bits/stdc++.h> using namespace std; signed main() { ios_base::sync_with_stdio(false); cin.tie(0); int n, q; cin >> n >> q; vector<int> A(n + 1); for (int i = 1; i <= n; i++) cin >> A[i]; int k; while (Q--) { cin >> k; auto p = lower_bound(A.begin(), A.end(), k); if (p != A.end() && *p == k) cout << p - A.begin() << '\n'; else cout << "-1\n"; } return 0; } ``` ---- ### upper_bound ```cpp= vector<int> v = {1, 2, 3, 5, 6}; cout << upper_bound(v.begin(), v.end(), 2) - v.begin() << '\n'; // -> 2 cout << upper_bound(v.begin(), v.end(), 0) - v.begin() << '\n'; // -> 0 cout << upper_bound(v.begin(), v.end(), 4) - v.begin() << '\n'; // -> 3 cout << upper_bound(v.begin(), v.end(), 7) - v.begin() << '\n'; // -> 5 // upper_bound回傳第一個「大於」x的元素的iterator ``` ---- ### lower_bound for set / map ```cpp= set<int> st = {1, 2, 3, 5, 6}; auto p1 = st.lower_bound(2); /// *p == 2 auto p2 = st.lower_bound(0); /// *p == 1 auto p3 = st.lower_bound(4); /// *p == 5 auto p4 = st.lower_bound(7); /// p == st.end() ``` --- ## 東方古墓古文 給一長度為 $N\ (N \le 10^5)$ 的正整數陣列 $t$， 將 $t$ 分成 $M$ 段連續的子陣列， 求各段子陣列中總和最大的一段的最小可能值 ---- 範例：$N=5, M=3, t=[1, 2, 3, 4, 5]$ * $[1, 2], [3, 4], [5]$ → $3, 7, 5$ → 最大值為 $7$ * $[1], [2, 3], [4, 5]$ → $1, 5, 9$ → 最大值為 $9$ * $[1, 2, 3], [4], [5]$ → $6, 4, 5$ → 最大值為 $6$ ---- 轉換問題： 能否將 $t$ 分成 $M$ 段總和不超過 $K$ 的連續子陣列？ ---- 若 $t_i > K$ 則一定不能， 否則使用貪心法最小化用到的子陣列數量： * 若數字加入前一段總和不會超過 $K$ 則加入 * 否則設為新的一段 ---- ```cpp= if (maxt > K) // maxt 為 t[i] 的最大值 cout << "NO\n"; else { int now = 0, cnt = 1; for (int i = 0; i < N; i++) if (now + t[i] <= K) now += t[i]; else now = t[i], cnt++; if (cnt <= M) cout << "YES\n"; else cout << "NO\n"; } ``` ---- 回到原問題： 將 $t$ 分成 $M$ 段連續子陣列， 求最大的子陣列總和的最小可能值 $ans$ ---- 能否將 $t$ 分成 $M$ 段總和不超過 $K$ 的連續子陣列？ → $K$ 越小，需要的子陣列越多 → 求最小的 $K$ 使得子陣列數量不超過 $M$ **二分搜** ---- ```cpp= #include<bits/stdc++.h> using namespace std; int N, M; vector<int> t; bool chk(int K) { int now = 0, cnt = 1; for (int i = 0; i < N; i++) if (now + t[i] <= K) now += t[i]; else now = t[i], cnt++; return (cnt <= M); } signed main() { ios_base::sync_with_stdio(false); cin.tie(0); cin >> N >> M, t.resize(N); for (int i = 0; i < N; i++) cin >> t[i]; int mx = 0; for (int i = 0; i < N; i++) mx = max(mx, t[i]); int l = mx - 1, r = 1000000000; while (l + 1 != r) { int K = l + (r - l) / 2; if (chk(K)) r = K; else l = K; } cout << r << '\n'; return 0; } ``` --- ## 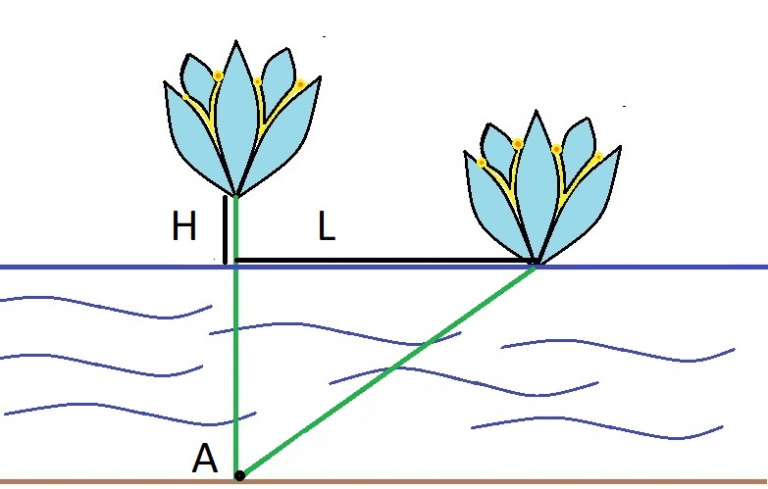Water Lily (CF 1199B)  ---- 簡化題目：  給$H=\overline{BC}$，$L=\overline{CD}$， 已知$\overline{AB}=\overline{AD}$，求$\overline{AC}$長度 答案誤差需小於$10^{-6}$ ---- $\overline{AC}^2 + L^2 = \overline{AD}^2$ $=(\overline{AC} + H)^2$ → 對$\overline{AC}$長度進行二分搜 ---- ```cpp= #include<bits/stdc++.h> using namespace std; signed main() { ios_base::sync_with_stdio(false); cin.tie(0); double h, l; cin >> h >> l; double a = 0, b = 1e12; // AC線段長度左右界 while (b - a > 1e-6) { double m = (a + b) / 2; if (pow(m, 2) + pow(l, 2) < pow(m + h, 2)) b = m; else a = m; } cout << fixed << setprecision(16) << a << '\n'; // 輸出至小數後16位減少誤差 return 0; } ```