---
tags: 機器學習技法
---

Ch1 Linear SVM
===

## Content
[TOC]

## [Slides & Videos](https://www.csie.ntu.edu.tw/~htlin/mooc/)

## [Large-Margin Separating Hyperplane](https://www.youtube.com/watch?v=8hak0XngnV0&list=PLXVfgk9fNX2IQOYPmqjqWsNUFl2kpk1U2&index=2)

### Which Line Is Best?
- 就我們之前推導的 VC bound 來看，這三條線好像沒什麼差？

### Why Rightmost Hyperplane
<!--  -->
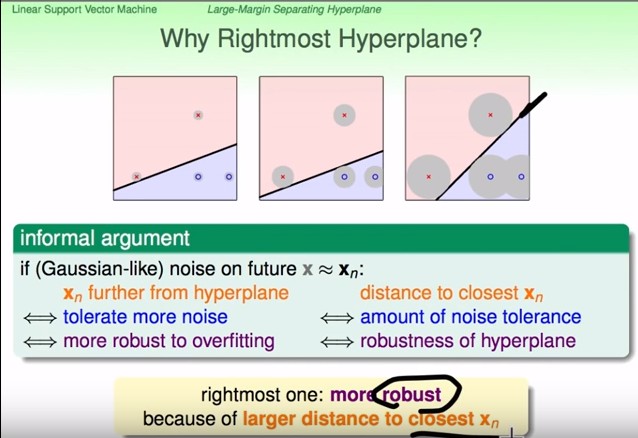- 在用一條線把資料點分開時，prefer最大空隙的那條線，因為這樣可以容忍最大的**測量誤差(針對 feature)**
- 之前說過，noise 會造成 overfitting，所以越能容忍 noise 的線，應該要越好

### Fat Hyperplane
- 也就是說我們要找到 離最近的$x_n$ 距離最遠 的那條線，最胖的那條線

### Large-Margin Separating Hyperplane
<!--  -->
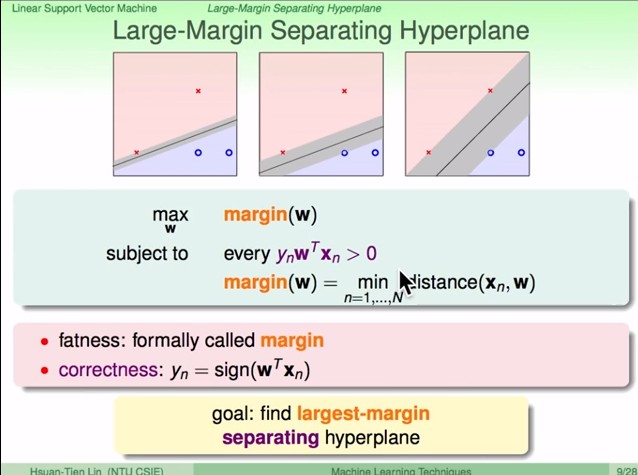- 假設我們資料真的是 linear separable
- **fatness**：正式名稱其實是 **margin**，離 hyperplane 最近的點和 hyperplane 的距離
- $margin(w) = \min_\limits {n=1,...,N}\ distance(x_n,w)$
- **correctness**: 預測出來的結果和 $y_n$ 同號，即 $y_nw^Tx_n>0$
- 於是我們有了最佳化問題
- 目的是 $\max_\limits w margin(w)$
- $margin(w) = \min_\limits {n=1,...,N}\ distance(x_n,w)$
- 條件是 $y_nw^Tx_n>0,\forall (x_n,y_n)\in\mathcal D$
- 這樣的問題看似難解，接下來就要把它轉換成我們會解的 optimization problem

<!--  -->
<!--  -->
- v 是一個二維向量 $(v_1,v_2)$，資料點$(v_1,v_2)$ 是+1，點$(-v_1,-v_2)$ 是-1，找出可以分開這兩個資料點並且有最大margin的 Hyperplane
- 就是求 $v$ 和 $-v$ 的中垂線，即 $v_1x_1+v_2x_2=0$

## [Standard Large-Margin Problem](https://www.youtube.com/watch?v=lHo9GcIURRs&list=PLXVfgk9fNX2IQOYPmqjqWsNUFl2kpk1U2&index=3)

### Distance to Hyperplane: Preliminary
<!--  -->
- 既然要求 margin，那就要先來看看「距離」該怎麼算
- 現在開始把 $w_0$ 跟 $x_0$ 簡化成 $b$，以便之後計算距離 (跟前面還有基石課用的 notation 不一樣)

### Distance to Hyperplane
<!--  -->
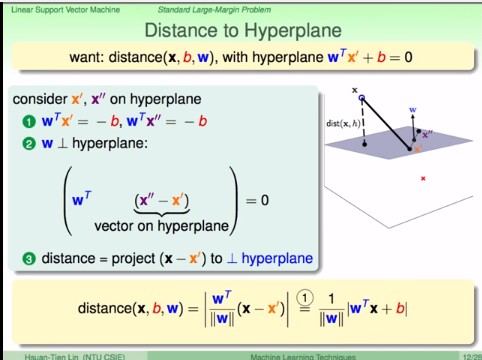- 若有任意兩個點 $x',x''$ 都在 hyperplane $w^Tx+b=0$ 中
- 我們知道 $w^Tx'=-b$ 且 $w^Tx''=-b$
- 所以 $w^T(x''-x')=0$
- 也就是說 vector on hyperplane 跟 $w$ 的內積會是 0
- 所以 **$w$ 向量垂直於這個平面，也就是 hyperplane 的法向量**
- 既然如此，那我要求 $x$ 到 hyperplane 的距離，其實就是 $x$ 到 hyperplane 上任意點 $x'$ 的向量，投影到 $w$ 上即可。
- $distance(x,b,w)=|\dfrac{w^T}{\|w\|}(x-x')|=\dfrac{1}{\|w\|}|w^Tx+b|$
- 只要回憶一下向量投影長公式 ($v_1$ 投影到向量 $v_2$) $\dfrac{v_1\cdot v_2}{\|v_2\|}=\dfrac{v_1^Tv_2}{\|v_2\|}=\dfrac{v_2^Tv_1}{\|v_2\|}$ 並利用 $w^Tx'=-b$ 即可得證。

### Distance to Separating Hyperplane
- 既然我們要的 hyperplane 是能夠切分所有 data 的，那就代表對任何第 $n$ 筆 data 來說 $y_n(w^Tx_n+b)>0$
- 所以 $|w^Tx_n+b|=y_n(w^Tx_n+b)$
- 這時候對任何第 $n$ 筆資料來說 $distance(x_n,b,w)=\dfrac 1{\|w\|}y_n(w^Tx_n+b)$
- 所以原本的 optimization problem 就變成了：
- 目的 $\max_\limits{b,w} margin(b,w)$
- $margin(b,w)=\min_\limits{n=1,...,N}\dfrac 1{\|w\|}y_n(w^Tx_n+b)$
- 條件 $y_n(w^Tx_n+b)>0,\forall (x_n,y_n)\in\mathcal D$

### Margin of Special Separating Hyperplane
- 既然對 $w,b$ 同時做縮放，不會影響 hyperplane，那麼乾脆讓最靠近 hyperplane 的點 $n$ 的 $y_n(w^Tx_n+b)=1$(本來可能等於 $k$ 之類的)，方便等等計算
- > Q: 這裡我一直以來就有一個疑問，既然 $w,b$ 縮放是不影響 hyperplane 的，那我對 linear classification model 做 weight-decay 的 regularization 是否就沒用，很久以前實務上有試過似乎的確得到這樣的結論...
- 這樣子我們的 margin 就可以簡化成 $\frac 1 {\|w\|}$ 了，nice
- 不過這樣就多一個條件，就是 $\min_\limits{n=1,...,N}y_n(w^Tx_n+b)=1$
- 有了這個條件，之前的條件 $y_n(w^Tx_n+b)>0,\forall (x_n,y_n)\in\mathcal D$ 一定會成立，所以不用再特別寫了。
- optimization problem 現在變成：
- 目標 $\max_\limits{b,w} \frac 1{\|w\|}$
- 條件 $\min_\limits{n=1,...,N}y_n(w^Tx_n+b)=1$
- 那麼U沒U更好解的條件ㄋ
- > meta-knowledge: 如果有些因素怎麼變動都無關緊要，那麼就可以對該因素做 constraint，這樣可能可以轉化問題?(變得比較好解?)

### Standard Large-Margin Hyperplane Problem
- 還是有點難解呢，又要 maximize，constraint 裡面又有 minimize 好煩哪，不如我們放寬一下條件吧？
- > Q: 為何 maximize 跟 minimize 同時解會很難解?
- 目標 $\max_\limits{b,w}\frac 1{\|w\|}$
- 本來條件 $\min_\limits{n=1,...,N}y_n(w^Tx_n+b)=1$ (灰色框框)
- 我們放寬成 $y_n(w^Tx_n+b)\geq 1,\forall (x_n,y_n)\in\mathcal D$ 吧？ (藍色大框框)
- 這個條件是本來條件的 necessary constraints (必要條件)
- 不對呀放寬條件就不是原本的條件了啊
- 只要證明放寬條件之後找到的 optimal point 還是會符合原本條件(落在灰色框框)就可以ㄌ！
- 來啊來證明
- 反證法
- 假設 optimal point $(b,w)$ 使得 $\min_\limits{n=1,...,N}y_n(w^Tx_n+b)=k>1$
- 那我把 $w$ 跟 $b$ 都除以 $k$ 就可以得到新的 optimal point 了啊，矛盾！
- 所以 optimal point $(b,w)$ 會符合原本條件 $\min_\limits{n=1,...,N}y_n(w^Tx_n+b)=1$ (灰色框框)
- 終於啊我可以放心的放寬條件了，把煩人的 minimize 拿掉！
- optimization problem 現在變成
- 目標 $\min_\limits{b,w} \frac 12w^Tw$
- 這裡我們把 maximize 改成 minimize，變得比較熟悉
- 條件 $y_n(w^Tx_n+b)\geq 1,\forall (x_n,y_n)\in\mathcal D$
- > meta-knowledge: 如果 constraint 裡面有 min/max，那麼可以放寬該 constraint，只要我們可以證明最後仍然會收斂到符合原本的 constraint 即可(利用 objective function 的特性)

### Fun Time: Large-Margin Hyperplane Problem

## [Support Vector Machine](https://www.youtube.com/watch?v=FAm70y081o4&list=PLXVfgk9fNX2IQOYPmqjqWsNUFl2kpk1U2&index=4)

### Solving a Particular Standard Problem
- 實際解一個例子看看
- $X=\begin{bmatrix}0&0\\2&2\\2&0\\3&0\end{bmatrix},y=\begin{bmatrix}-1\\-1\\+1\\+1\end{bmatrix}$
- 可以解得 $w_1\geq +1,w_2\leq -1$
- 所以 $\frac12w^Tw\geq 1$，也就是說再怎麼 minimize，最小就是 1
- 來試試看能不能做到最小吧！
- 我們就讓 $w_1=1, w_2=-1$ 結果發現 $b=-1$ 可以符合所有條件
- 我們最終得到的 function 就是 $g_{SVM}(x)=\text{sign}(x_1-x_2-1)$
- > Q: 等等這裡的 $x_1,x_2$ 應該還是指 feature 而不是第 1、2 筆資料吧？可是這樣 notation 就跟上面的 $y_n(w^Tx_n+b)$ 相違背啊！？
- 這跟 Support Vector 有啥關係?

### Support Vector Machine (SVM)
- 因為除了離邊界最近的點以外，都不會影響 hyperplane
- 這些點支撐著這條胖胖的線，所以被稱為 support vector (支撐向量)
- 之後會提到這些點其實是 support vector 的 candidate(候選人)
- SVM 就是利用 support vectors 去找一個最 fat 的 hyperplane

### Solving General SVM
- 前面是解 specific 的 SVM，那 general case 怎解呢？
- gradient descent? 有限制(constraints)的問題很難用 GD 解。
- 不過很幸運的這個問題有兩個特性
- 它的 **objective function 是 quadratic (convex) 的**
- 它的 **constraint 是 linear 的**
- **有以上兩個特性，就是一個 quadratic programming (二次規劃) 的問題**

### Quadratic Programming
- 左邊是我們本來的 optimization problem
- 右邊就是 quadratic programming 的其中一種形式
- 符合這個形式的問題就可以直接利用 qudratic programming 的工具來解。
- 我們可以把左邊的東西寫成下面的樣子，就完全符合 quadratic programming 的形式

### SVM with QP Solver (Linear Hard-Margin SVM)
- hard-margin 意思是我們要把所有資料都分開

### Fun Time: SVM with QP Solver

## [Reasons behind Large-Margin Hyperplane](https://www.youtube.com/watch?v=7UUO_AamxcA&list=PLXVfgk9fNX2IQOYPmqjqWsNUFl2kpk1U2&index=5)

### Why Large-Margin Hyperplane?
- 這邊 linear hyperplane 也可以應用在 non-linear transform 的 feature 上，所以先用 $z$ 來通用表示我們的 feature
- 仔細觀察 weight-decay regularization 和 SVM 的異同
- regularization
- 目標 minimize $E_{in}$
- 條件 $w^Tw\leq C$
- SVM
- 目標 minimize $w^Tw$
- 條件 $E_{in}=0$ (而且要求 $\min_\limits n y_n(w^Tz_n+b)=1$)
- 所以 SVM 可以想成是一種 regularization

### Large-Margin Restricts Dichotomies
- 以 VC dimension 的方式來說明
- PLA 可以 shatter 最多 3 個點 (他可以做出所有 8 種 dichotomies)
- 可是 SVM 你限制它的 margin 一定要大於 $\rho$ 的時候，可能就有某些 case 是它不能做出的 dichotomy
- 所以它 VC dimension 比較小，那 generalization 能力就比較好

### VC Dimension of Large-Margin Algorithm
- 那我們來看看「喜歡胖子(margin 超過 $\rho$)的演算法 $\mathcal A$」的 VC dimension 是多少唄
- !!?? 不是應該是 hypothesis set 才能算 VC dimension 嗎?
- 還要考慮演算法在這個資料上做不做得到
- > Q: 這邊沒看很懂 ㄎㄎ 改天再看一次
- 總之這樣的演算法 VC dimension $d_{VC}(\mathcal A_\rho)$ 就是可以比 $d+1$ 還要小啦，爽

### Benefits of Large-Margin Hyperplanes
- 使用 large-margin 加上 non-linear transform 可以結合兩者優點

### Fun Time: VC Dimension of Large-Margin Algorithm
- 這個好像要懂前面那個證明才會R，下次再看

### Summary