---
tags: 機器學習基石上：數學篇
---

Ch6 Theory of Generalization
===

## Content
[TOC]

## [Slides & Videos](https://www.csie.ntu.edu.tw/~htlin/mooc/)

## [Restriction of Break Point](https://www.coursera.org/learn/ntumlone-mathematicalfoundations/lecture/xCgtg/restriction-of-break-point)

### Review: The Four Break Points
複習：
- $m_\mathcal H(N)$：$N$ 個 datapoints 時，hypothesis set $\mathcal H$ 所能切出的最多 dichotomies 數量
- minimum break point $k$：就是 $m_\mathcal H(k)<2^k$ 的第一個點
- 露出一線曙光的那個點

### Restriction of Break Point
- 當我們說 **minimum break point 是 2，代表任何兩筆 data 都不能被 hypothesis set $\mathcal H$ 給 shatter，所以接下來的推導都不能違反這個規則**
- > Q: slide 上怎麼寫 every 啊？ $m_\mathcal H(N)$ 不是已經是固定的 maximum number of dichotomies 了嗎
>> 可能因為 $\mathcal H$ 沒固定吧，因為這裡應該是指所有 minimum break point $k=2$ 的 $\mathcal H$
- 那麼來看看，在最小 Break Point $K = 2$ , 資料數量 $N = 3$ 的情況下，最多可以產生多少種 dichotomy
- 前提是必須符合前面說的「任意兩個 datapoints 都不能 shatter」的條件，也就是說 $\mathcal H$ 不得 shatter $(x_1,x_2)$ 或 $(x_1,x_3)$ 或 $(x_2,x_3)$
- 這 1 個 dichotomy 沒問題
- 
- 這 2 個 dichotomies 也沒問題
- 
- 這 3 個 dichotomies 也沒問題
- 
- 嘖嘖，這 4 個 dichotomies 出問題了，因為 $\mathcal H$ shatter 了 $(x_2,x_3)$，所以我們要選別的 dichotomy set
- 
- 換成這 4 個 dichotomies 就沒問題
- 
- 我們會發現第 5 個 dichotomy 不論怎麼選，都會造成有兩個 data point 被 shatter
- 
- 
- 
- 
- 從上述分析可以得知，\(在二元分類問題中\) 若 $k=2$ (hypothesis set 不能 shatter 任意 2 筆資料)，結果會是：**在 $N=3$ 的時候，我們最多最多就只能有 4 種 dichotomies。**

### Restriction of Break Point - Idea
- 從前面的結論來看，當 minimum break point $k=2$ 時：
- 當 $N=1$，則 $m_\mathcal H(N)=2$，也就是最多可以有 2 種 dichotomies
- 當 $N=2$，則 $m_\mathcal H(N)$ 的 **maximum possible value** 是 $3$ (因為若是 $4$ 的話就 shatter 了，矛盾)
- 當 $N=3$，則 $m_\mathcal H(N)$ 的 **maximum possible value** 是 $4$，這是剛剛推導出來的
- 從前面的推導可以得知，一旦 $N$ 越過 minimum break point $k$，就會讓前面的「不準 shatter 任何 $k$ 個點」的規範，去對未來的 dichotomies 的最多可能的數量加上了很大的限制 (因為每個排列組合都要考量到不能 shatter 任何 $k$ 個點)
- 換句話說，就是 $m_\mathcal H(N)$ 的 maximum possible value 就受到了很大的限制
- **Idea: 那我們不如利用這樣的性質來算算看，$m_\mathcal H(N)$ 的 maximum possible value 會是多少，如果它也是個多項式的話，我就可以放心大膽的說，我的 $m_\mathcal H(N)$ 也是一個多項式**

### Fun Time: Maximum Possible $m_\mathcal H(N)$

## [Bounding Function: Basic cases](https://www.coursera.org/learn/ntumlone-mathematicalfoundations/lecture/VvtNT/bounding-function-basic-cases)

### Bounding Function

- 可以先回顧上一節的 [idea](https://hackmd.io/k00DVu6hQ2-TY0gCvTD81Q?both#Restriction-of-Break-Point---Idea)
- Bounding Function $B(N,k)$ : 當最小的 Breaking Point 是 $k$，則在 $N$ 筆資料時「最多可以容納」多少種 dichotomies？即成長函數 $m_\mathcal H(N)$ 的上界。
- 瘋狂地做上界ㄟ傻眼
- $B(N,k)$ 是 $m_\mathcal H(N)$ 的 upper bound
- $m_\mathcal H(N)$ 又是 $\mathcal H$ 能做出的 dichotomies 數量的 upper bound

### Table of Bounding Function

<!--  -->

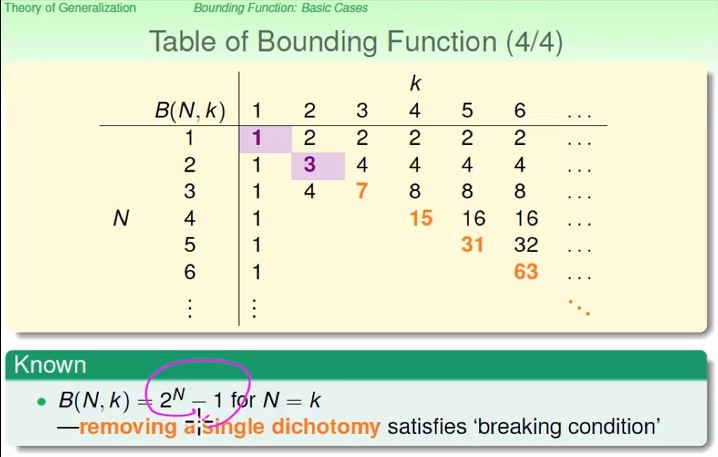* 在 $k=1$ 時，$B(N,k) = 1$
* 回想上一個 Fun Time (連一個點都不能 shatter)
* 在 $N<k$ 時，$B(N,k) = 2^N$
* 因為 minimum break point 是 $k$，所以當 $N<k$ 時，任意 $N$ 個點都可以 shatter (可複習前面)
* 在 $N=k$ 時，$B(N,k) = 2^N-1$
* 因為 minimum break point 是 $k$，所以當 $N=k$，則任意 $N$ 個點都不能 shatter，所以最多只能產生 $2^N-1$ 種 dichotomies (可複習前面)

### Fun Time: Bounding Function
- $B(4,4)$ (upper bound) 是 15，不過實際上 $m_\mathcal H(4)$ 是 14

## [Bounding Function: Inductive Cases](https://www.coursera.org/learn/ntumlone-mathematicalfoundations/lecture/Y0cRD/bounding-function-inductive-cases)

### Estimating B(4,3)
- 我們可以推測也許 $B(4,3)$ 會和 $B(3,?)$ 有關

### Peek the Answer of B(4,3) is 11
- 先用暴力法搜尋了一下最多種的 dichotomies 發現 $B(4,3)=11$
- 那也許規則就是，$B(N,k)$ = 它的上方數字加上它的左上數字?

- 我們把 $x_1,x_2,x_3$ 和 $x_4$ 拆開來看，可以分出成雙成對的 $2\alpha$ 個，和形單影隻的 $\beta$ 個，總共 $2\alpha+\beta$ 種 dichotomies

- 如果我們把 $x_4$ 遮掉不看，總共就只有 $\alpha+\beta$ 種 dichotomies
- 但是 $B(4,3)$ 有個條件啊就是 $k=3$，任何 3 個點不能 shatter，所以 $\alpha+\beta\leq B(3,3)$ 必須成立。

- 我們再次把 $x_4$ 遮掉，只看 $x_1,x_2,x_3$，而且不看紫色部分，這樣總共有 $\alpha$ 種 dichotomies
- 那我們如果在 $x_1,x_2,x_3$ 當中 shatter $2$ 個點會發生啥事咧？
- 注意喔橘色的這些東西是成雙成對的，所以對於所有這些 dichotomies，$x_4$ 都有 o 有 x
- 啊那不就代表我們 shatter 了 $2+1=3$ 個點嗎？乾死定了！
- 所以這 $\alpha$ 個 dichotomies 不能 shatter 任何兩個點，結果就是 $\alpha\leq B(3,2)$ 必須成立。

### Putting It All Together

<!--  -->
- 用相同的證明方式，可以得知
- $\alpha+\beta\leq B(N-1,k)$
- $\alpha\leq B(N-1,k-1)$
- 我們終於可以填表了，只是填的不是 bounding function，而是它的上限(ㄎㄅ又是 upper bound)，也就是說，表中任一數值的上限為其上方和左上方數值之和。

- 最後我們可以得到 $B(N,k) \leq \sum\limits_{i=0}^{k-1}C_i^N$, 這會是一個N的多項式，太棒ㄌ
- 最高次項是 $N^{k-1}$

- 本來我們沒辦法寫出 2D perceptron 的 growth function $m_\mathcal H(N)$，但是現在我們找到了它上限的上限！
- 不知道成長函數沒關係，只要我們找得到 $\mathcal H$ 的 minimum break point $k$，就可以得到上限的上限。

### Fun Time: Upper Bound of the Bounding Function

## *[A Pictorial Proof](https://www.coursera.org/learn/ntumlone-mathematicalfoundations/lecture/kVwun/a-pictorial-proof)

### 實際上這個公式還會多出一些有的沒的常數
- 接下來要用形象化的方式(不那麼數學)來證明這些常數怎麼跑出來的

<!--  -->
<!--  -->
<!--  -->
<!--  -->
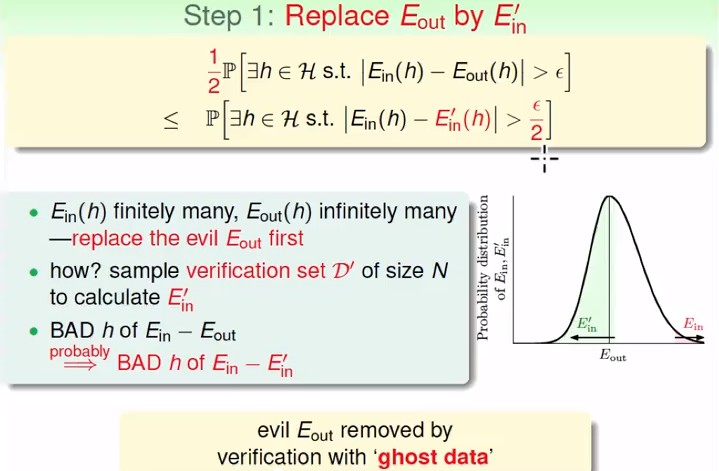
- 我們之前所做的這些只是讓 $E_{in}(h)$ 變成有限多個，但實際上 $E_{out}(h)$ 還是無限多個RRR
- 但是我們想把 $E_{out}$ 變成有限的, 所以抽另外一組資料 $D'$，用我們之前說的 verification 計算 ${E_{in}}'$ 來估計 $E_{out}$
- 所以把後面的 $E_{out}$ 帶換成 $E_{in}'$
- 這裡 $D'$ 被稱為 ghost data，因為它並不真的存在，而只是我們自己想像若再抽一把資料，會發生什麼事情。
- 若使用各種 dataset 來計算各種 $E_{in}$ 和 ${E_{in}}'$ 則這些 $E$ 的分布會如上圖右, 那麼在壞事情\($E_{in}$ 和 $E_{out}$ 離很遠\)發生的時候, $E_{in}$ 和 ${E_{in}}'$ 有超過 1/2 的機率也會離很遠。
- 所以在最前面加上了一個 1/2
- 另外我也希望如果是計算 $E_{in}$ 跟 $E_{in}'$ 的差距，那我條件要稍微嚴苛一點
- 所以後面的 $\epsilon$ 乘上 1/2

<!--  -->
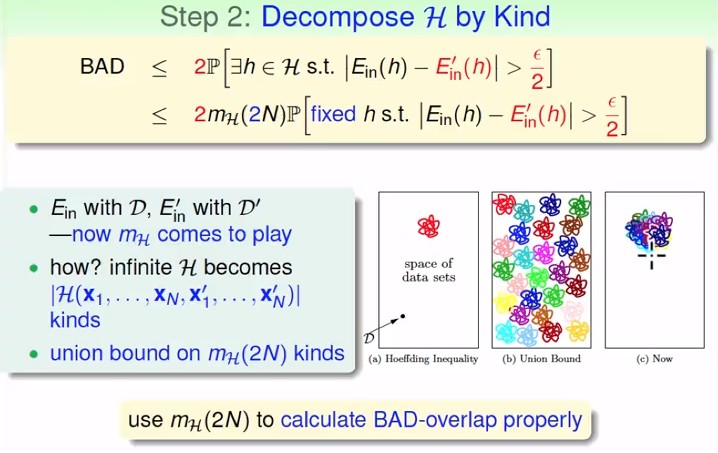- 剛剛把 $E_{out}$ 換成 $E_{in}'$ 就是為了把它變有限多種，現在是時候出手ㄌ
- $D$ 有 $x_1$ 到 $x_N$；$D'$ 有 ${x_1}'$ 到 ${x_N}'$, 我們本來有無限的 $\mathcal H$，而現在只需要計算 $\mathcal H(x_1,...,x_N,{x_1}',...,{x_N}')$ 可以分出多少種 dichotomies，即 $m_\mathcal H(2N)$

>***Q: 這附近怎麼開始有點聽不懂在工殺虫 是我發高燒到腦袋燒壞了嗎***

<!--  -->

* $|E_{in}-{E_{in}}'|$ : $E_{in}$ 跟 ${E_{in}}'$ 的差別
* $|E_{in}-\frac{E_{in}+{E_{in}}'}{2}|$ : $E_{in}$ 跟所有人的差別
* 所以用 $\epsilon /4$ 代入Hoeffding

### Vapnik-Chervonenkis \(VC\) bound
<!--  -->

### Fun Time: VC bound
- 從題目可以發現這個bound並不是這麼準, 下堂課會探討為啥明明不準還要推導這個bound, 還有要如何利用break point。

<!--  -->
- 下次會來說明我們在實務上要怎麼利用 break point。