---
tags: 機器學習基石上：數學篇
---

Ch7 VC Dimension
===

## Content
[TOC]

## [Slides & Videos](https://www.csie.ntu.edu.tw/~htlin/mooc/)

## [Definition of VC Dimension](https://www.coursera.org/learn/ntumlone-mathematicalfoundations/lecture/AnYJ6/definition-of-vc-dimension)

### Recap: More on Growth Function
- 成長函數的上限的上限是 $N^{k-1}$

### Recap: More on Vapnik-Chervonenkis (VC) Bound

### VC Dimension Definition
<!--  -->
- **最大的 non- break point 為 $k-1$，即 VC Dimension，$d_{VC}$**
- $d_{VC} = \min(k) - 1$
- $H$ 能夠 shatter 的最多 input
<!--  -->
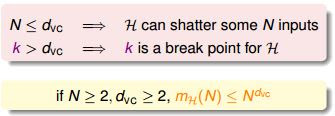- $\mathcal H$ 可以 shatter 最多 $d_{VC}$ 個資料點，但不是任意 $d_{VC}$ 個資料點都能被 $\mathcal H$ 給 shatter
- 比 VC dimension 大，就是 break point 所以叫 $k$
- 當 $N$ 夠大且 $d_{VC}$ 也夠大時，成長函數會比 $N$ 的 VC dimension 次方來得小
- 當 $N\geq 2$ 且 $\min(k)\geq 3$(即 $d_{VC}\geq 2$)，$m_\mathcal H(N)\leq N^{d_{VC}}$

> Q: 感覺教授這附近對 $k$ 的定義有時候是 minimum break point，有時候是任何 break point...

### VC Dimensions: 4 examples
- 之前我們說，有露出一線曙光的點 (break point)，才是好的 hypothesis set
- 對應到這裡就是，VC dimension 是 finite 的 hypothesis set 才是好的 $\mathcal H$


### Fun Time: VC Dimension

## [VC Dimension of Perceptrons](https://www.coursera.org/learn/ntumlone-mathematicalfoundations/lecture/l89CH/vc-dimension-of-perceptrons)

### 2D PLA Revisited

### 證明 PLA 在資料維度為 d 時, VC Dimension 是 d+1
- 證明 $d_{VC} \geq d+1$, 只要找到一種 $d+1$ 筆的資料是可以被 PLA 給 shatter 的即可
- 證明 $d_{VC} \leq d+1$, 需要證明對於任何 $d+2$ 筆的資料, PLA 都不能夠 shatter

### 證明 $d_{VC}\geq d+1$
- 剛剛我們說，證明 $d_{VC} \geq d+1$, 只要找到一種 $d+1$ 筆的資料是可以被 PLA 給 shatter 的即可
- 我們現在找到這組特別的 input，使得 $X$ 是可逆矩陣
- 注意這裡插入了常數項 $x_0=1$

- 想要 shatter 這 $d+1$ 個點，代表 $y$ 不論長什麼樣子都要成立 $\text{sign}(Xw)=y$
- 既然 $X$ 是可逆的，那其實就可以直接解 $w$ 使得 $Xw=y$ 因為這樣也可以成立 $\text{sign}(Xw)=y$
- 不論 $y$ 是多少，都能解得 $w=X^{-1}y$
- 所以這 $d+1$ 個點可以被 shatter，代表 $d_{VC}\geq d+1$

### 證明 $d_{VC}\leq d+1$
- 剛剛我們說，證明 $d_{VC} \leq d+1$, 需要證明對於任何 $d+2$ 筆的資料, PLA 都不能夠 shatter
- 先來看 2D 的 case
- 
- 現在 $x_1=\begin{bmatrix}0\\0\end{bmatrix}, x_2=\begin{bmatrix}1\\0\end{bmatrix}, x_3=\begin{bmatrix}0\\1\end{bmatrix}$ 這三個點可以 shatter
- 但是加入了第四個點 $x_4=\begin{bmatrix}1\\1\end{bmatrix}$ 就沒辦法 shatter 了，因為以圖為例的話，它(問號)是 x 的情況是沒辦法被 perceptron 分開，但是數學上為什麼沒辦法做出這種 dichotomy 呢?
- 我們知道 $x_4=x_2+x_3-x_1$，所以 $w^Tx_4=w^Tx_2+w^Tx_3-w^Tx_1$
- 那麼當 $w^Tx_2>0$ 且 $w^Tx_3>0$ 且 $w^Tx_1<0$ 的時候，$w^Tx_4$ 就一定大於 0，它不可能小於 0，所以第 4 個點它沒辦法 shatter
- 結論是 linear dependence 限制了 dichotomies 的數量
- 但這只是一個特殊的例子，我們要證明對所有 $d+2$ 筆資料都不能 shatter
- 推廣到 $d$ 維的 case
- 
- 現在列出來可以發現 $X \in \mathbb R^{(d+2)\times (d+1)}$，$X$ 有 $d+2$ 個 rows、$d+1$ 個 columns
- 線性代數告訴我們，這時候會有 linear dependence，$x_{d+2}$ 一定可以表示成其他 $x_1,...,x_{d+1}$ 的 linear combination $x_{d+2}=a_1x_1+...+a_{d+1}x_{d+1}$
- 所以 $w^Tx_{d+2}=a_1w^Tx_1+...+a_{d+1}w^Tx_{d+1}$
- 觀察一下會發現(圖較清楚)，我們沒辦法產生這種 dichotomy $(\text{sign}(a_1),\text{sign}(a_2),...,\text{sign}(a_{d+1}),-1)$，因為若前面的 sign 條件都滿足了，那麼 $w^Tx_{d+2}$ 一定會大於 0。
- 所以我們證明了 $d$ 維 perceptron 沒辦法 shatter 任何 $d+2$ 個 datapoint。

## [Physical Intuition of VC Dimension](https://www.coursera.org/learn/ntumlone-mathematicalfoundations/lecture/z3Caf/physical-intuition-of-vc-dimension)

### Degrees of Freedom
- VC dimension 的物理意義
- 對 binary classification 來說，有多少個旋鈕是我可以自由操控的
- **effective 'binary' degrees of freedom**
- 這個 hypothesis set $\mathcal H$ 到底強不強

- 實務上，如果想要估計 VC dimension，那麼去看看有多少個可調的旋鈕會是一個不錯的方式。

### $M$ and $d_{VC}$
<!--  -->
- 和 M 一樣, VC Dimension 不論太大或太小都不好, 因此要選擇一個好的 VC Dimension

### Fun Time: Degrees of Freedom
- 用自由度的角度看 VC dimension，馬上可以知道答案

## [Interpreting VC Dimension](https://www.coursera.org/learn/ntumlone-mathematicalfoundations/lecture/KAg9C/interpreting-vc-dimension)

<!--  -->
- 假設壞事情($E_{in}$ 和 $E_{out}$ 差很多) 發生的機率為 $\delta = 4(2N)^{d_{VC}}exp(-\frac{1}{8}\epsilon^2N)$
- 我們可以推導出 $\epsilon=\sqrt {\frac{8}{N}ln(\frac{4(2N)^{d_{VC}}}{\delta})}$

- 我們在乎的 **generalization error** $|E_{in}(g)-E_{out}(g)|$ 有 $1-\delta$ 的機率小於等於 $\epsilon$
- 也就是說我們有 $1-\delta$ 的**信心水準**使得 $E_{out}$ 會落在 $[E_{in}-\sqrt {\frac{8}{N}ln(\frac{4(2N)^{d_{VC}}}{\delta})}, E_{in}+\sqrt {\frac{8}{N}ln(\frac{4(2N)^{d_{VC}}}{\delta})}]$ 內
- 那通常我們比較在意 worst case，所以只看右邊那項。
- 根號裡面那些東西，我們通常叫它 **model complexity**
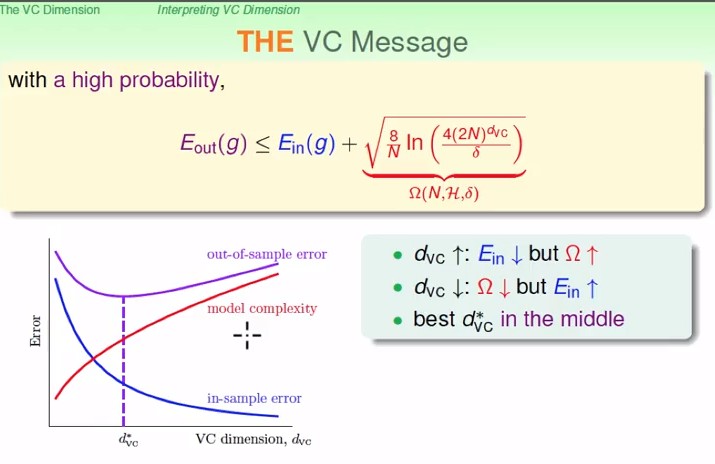
- 教授說 $\Omega(N,\mathcal H,\delta)=\sqrt {\frac{8}{N}ln(\frac{4(2N)^{d_{VC}}}{\delta})}$ 那也就是說 $\epsilon=\Omega(N,\mathcal H,\delta)$ 的意思囉
- 這裡的 $\sqrt {\frac{8}{N}ln(\frac{4(2N)^{d_{VC}}}{\delta})}$ 也就是我們付出的penalty, 而這個penalty會隨著 model的強大(VC Dimension的提高)而變得更大
<!--  -->
<!--  -->
- 隨著 VC dimension 越來越大，
- model complexity 也會越大
- in-sample error $E_{in}$ 會越小
- $E_{out}$ 先減後增
- **powerful $\mathcal H$ is not always good!**

### VC Bound Rephrase: Sample Complexity
- VC Bound 還有另外一個意思，樣本複雜度(sample complexity) 或稱資料量的複雜度
- 如果今天老闆開給你一個 spec 說，我只容許 0.1 的誤差，然後希望壞事情的機率不要超過 0.1，然後用 perceptron 來做，那多少 data 才夠呢?
- 真的去套公式算這個 $N$ 大約會是 10000倍的 VC dimension 才夠
- 但實務上我們發現 10 倍的 VC dimension 基本上就夠了，所以我們發現 VC bound 其實是非常非常寬鬆的

### 為何 VC Bound 這麼寬鬆?
- 我們用了 Hoeffding
- 它適用任何 distribution 以及任何的 target function
- 我們用了 growth function
- 適用任何 data
- 用了 $N^{k-1}$
- 適用任何 minimum break point 是 $k$ 的 hypothesis set $\mathcal H$ ($d_{VC}=k-1$)
- 用了 union bound
- 計算 worst case，說我們不準讓 algorithm 踩到雷(回想 BAD 表)，但其實偶爾踩到也沒關係的(?)

### Summary
<!--  -->
- 本週重點
- VC dimension = **maximum non-break point**
- $d_{VC}(\mathcal H)$ for perceptron is $d+1$
- VC dimension is approximate to **# free parameters**
- **model complexity**: how strong is $\mathcal H$ proper?
- **sample complexity**: how many data do we need?
- 目前都是在做 **沒有 noise 的 binary classification**，下周會延伸到更多的 learning 問題上。