## LTE: Lightweight and Time-Efficient Hardware Encoder for Post-Quantum Scheme HQC <br /><br /> *M11317004 蘇祐民* --- ### 目錄 - HQC簡介 - HQC簡化的計算過程 - HQC訊息編碼 - 論文實作 - 論文比較 --- ### Hamming-Quasi Cyclic > 基於漢明距離的準循環碼 ---- ### 基本介紹 1. 為NIST在PQC標準化過程的第四輪方案之一 2. 已確定會作為Kyber(FIPS 203)的替代方案 3. 基於**編碼理論**的密碼系統，其安全性基於**解碼隨機準循環碼**的難度 4. 使用兩種主要編碼： - Reed-Solomon與Reed-Muller串聯碼：用於訊息編碼和錯誤糾正 - 準循環碼：提供密碼系統所需的結構和安全性 ---- ### HQC的特點（正面） 1. 多樣性(非像Kyber是Lattice based) 2. 很小的私鑰大小(56~64 Bytes) 3. 高安全性保證(提供IND-CCA2級別的安全性，與Kyber相同) 5. 精確的解碼失敗率分析(小於 2^-128 至 2^-256) ---- ### HQC的特點（負面） 1. 較大的資源使用 - 公鑰(比Kyber大2-4倍) - 密文(比Kyber大3-9倍) 2. 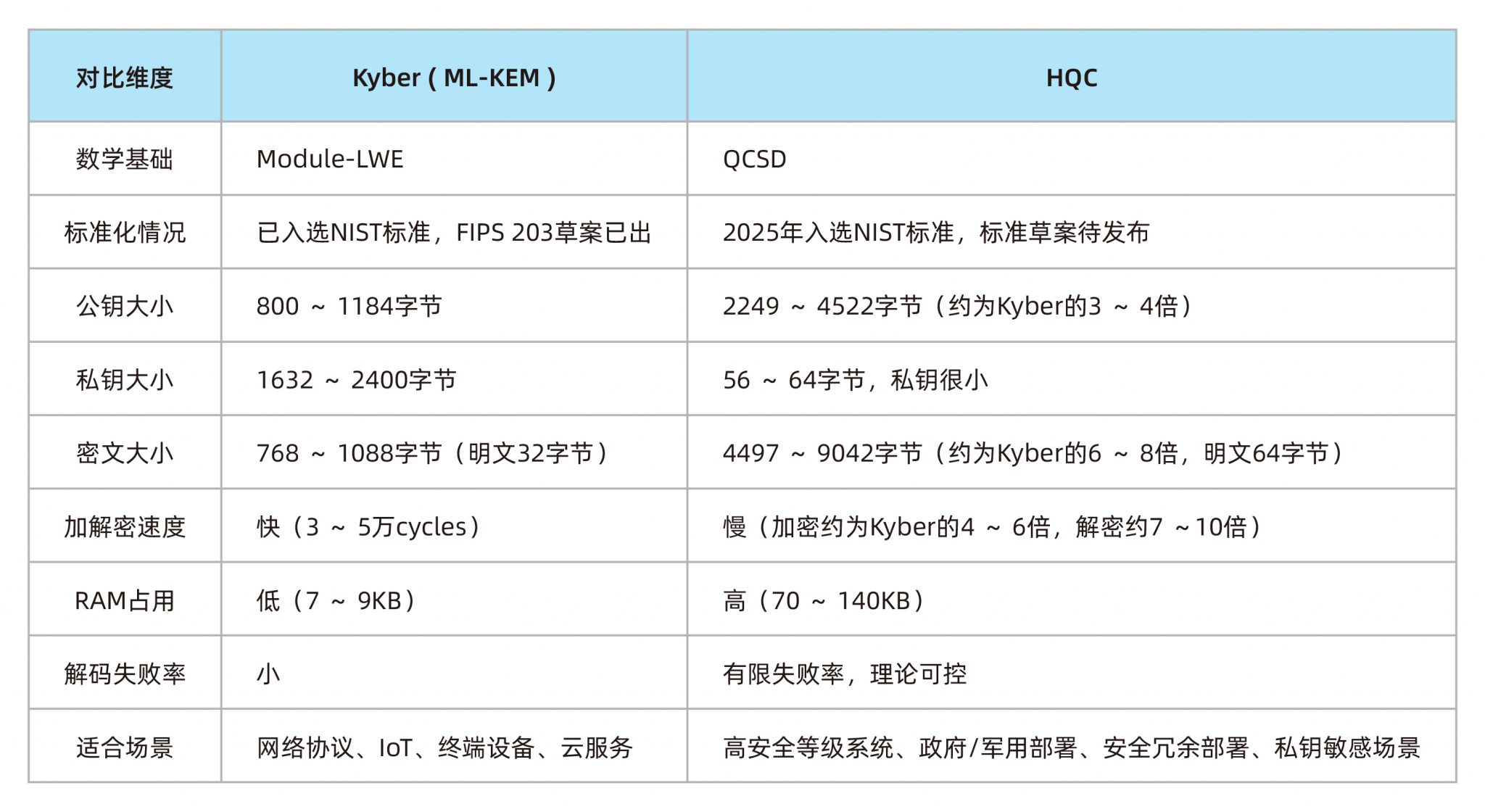計算速度較慢(相對Kyber在密鑰產生、封裝、解封裝都更久) ---- ### 比較表格  --- ### HQC計算過程 ---- ### 密鑰產生 1. 首先產生一個隨機向量<span class="red">`h`</span> 2. 接著產生兩個小權重向量<span class="red">`x`和`y`</span> 3. 公鑰是<span class="red">`(h, s = x + h * y)`</span> 4. 私鑰是<span class="red">`(x, y)`</span> ---- ### 資料加密 1. 將訊息`m`通過Reed-Solomon和Reed-Muller進行編碼 2. 產生小權重隨機向量<span class="red">`r1`, `r2`和`e`</span> 3. 計算<span class="red">`u = r1 + h * r2`</span> 4. 計算<span class="red">`v = 編碼(m) + s * r2 + e`</span><br/>(這裡引入了`噪聲`或`錯誤`) 5. 密文<span class="red">`c = (u, v)`</span> ---- ### 資料解密 1. 計算<span class="red">`v - u * y`</span> <br/>= <span class="red">`編碼(m) + (x * r2 - r1 * y + e)`</span> 2. 使用錯誤交糾正解碼器從中恢復原始訊息`m`<br/><span class="red">`(x * r2 - r1 * y + e)`</span>帶有刻意加入的`噪聲`或`錯誤` ---- ### 安全等級 就像AES有不同長度的版本，在HQC中也有這樣的設計： - hqc-128: 128bit，標準長度 - hqc-192: 192bit，更為安全 - hqc-256: 256bit，最安全 --- ### 訊息m的編碼過程 ---- ### 編碼流程 ```bash ┌─────────────┐ ┌──────────────┐ ┌─────────────┐ │ Message (m) ├──►│ Reed-Solomon │──►│ Reed-Muller │ └─────────────┘ └──────────────┘ └───────┬─────┘ ┌─────────────────────────────┘ ▼ ┌───────────────────────────────┐ ┌─────────────────┐ │ Repeat output multiple times ├──►│ Encoded Msg(mG) │ └───────────────────────────────┘ └─────────────────┘ ``` ---- ### Reed-Solomon 步驟  ---- ### Reed-Solomon 步驟  ---- ### Reed-Solomon 步驟  ---- ### Reed-Muller 步驟  ---- ### Reed-Muller 步驟  ---- ### Reed-Muller 步驟  ---- ### 重複輸出  ---- ### mG的產生  --- ### 論文實作 ---- LTE編碼器 > Lightweight and Time-Efficient ---- ### 主要貢獻 1. 設計出專用資料流，用於高效率處理HQC編碼過程中各次疊代之間的中間值 2. 分析並最佳化Reed-Solomon編碼器 3. 在FPGA上實現編碼器架構，並與最新的硬體實現進行比較 ---- ### 電路架構圖  ---- ### LTE 編碼器架構 - Reed-Solomon 編碼器 - Reed-Muller 編碼器 - 控制單元(Control Unit) ---- ### 編碼過程 1. 首先，Reed-Solomon編碼器啟動，並在k個週期內產生一個長度為n₁ Byte 的Reed-Solomon碼字 2. 該碼字被送入一個移位暫存器，然後以每個週期一個Byte的速率傳送到Reed-Muller編碼器 3. Reed-Muller編碼器將一個輸入的Byte轉換為一個128位元的碼字 ---- ### Reed-Solomon 編碼器  ---- ### Reed-Solomon 處理過程 1. 每次接收一個Byte的訊息，並與前一階段獲得的閘值進行XOR運算 2. 閘值被送入p個並行的Galois場乘法器 3. Galois場乘法器的輸出再次與線性反饋移位暫存器中的前一個碼字進行XOR運算 ---- ### RS編碼器中的Galois場乘法器最佳化 - `Arch.I` 基於列的傳統方法 - 一次讀取矩陣rot[a]的一列 - 計算rot[a]ᵢ·bᵢ - 累加結果以獲得最終答案 - 一次乘法需要8個週期完成 - `Arch.II` 基於全局優化的乘法 - 將所有涉及的乘法 轉換為輸入位元的線性組合 - **重用部分和** 來減少XOR閘的數量 - 允許Galois乘法器在一個週期內完成乘法 ---- ### Reed-Muller 編碼器  ---- ### 結果比較 - 兩種Galois乘法器的實作比較 - `Arch.II`與現有HQC編碼器的比較 ---- ### 元件說明: LUT - 功能：實現邏輯函數的基本元件 - 工作原理：本質上是一個小型的記憶體，儲存預先計算的結果 - 應用：可以實現任何數位邏輯功能（如AND、OR、XOR等邏輯門） - 簡單理解：可以想像成一個小型的真值表，輸入某個組合，立即輸出對應的預先設定好的結果 ---- ### 元件說明: FF - 功能：儲存一位元(1-bit)的資訊 - 工作原理：在時脈訊號的控制下捕獲並保持數據 - 應用：用於建立暫存器、計數器和狀態機 - 簡單理解：就像一個微小的記憶體單元，能夠記住一個位元的資訊直到下次被更新 ---- ### 元件說明: BRAM - 功能：較大容量的內建記憶體資源 - 工作原理：組織成固定大小的記憶體塊 - 應用：儲存較大量的數據，如查找表、緩衝區或小型內嵌式記憶體 - 簡單理解：相當於FPGA內部的小型RAM，可以儲存更多資料而不需要使用外部記憶體 ---- ### 兩種Galois乘法器的實作比較  ---- ### `Arch.II`與現有HQC編碼器的比較  --- ### 論文比較 ---- ### 目前還沒有除了這一篇以外的硬體實作  --- ### 教師提問 ---- ### HQC在面對不同的安全等級時，私鑰長度是否有所不同？ 在前面的報告中沒有提及，但實際上不同的安全長度確實會有不同的私鑰長度，在計算上，會先基於SHAKE256函式產生出長度為40的Seed，再加上各自安全等級的長度，公式為<span class="red">`40 + k / 8`</span>，也因此，以hqc-128來說，`40 + 128 / 8 = 56`，可參考下一頁的圖表。 ---- ### HQC文件中提供的表格  --- ### 謝謝各位 (●'◡'●) <style> .red {color: OrangeRed;} </style>