# Basic Physics-Based Fluid Simulation Methods in Computer Graphic

## 0. Post Details

- Reference: [Wang et al., Physics-based fluid simulation in computer graphics: Survey, research trends, and challenges, 2024.](https://link.springer.com/article/10.1007/s41095-023-0368-y)
- Post by: Jedd Yang
- Date: 2025-08-12
- Keywords: computer graphics, physical simulation, fluid simulation, fluid coupling

## 1. Simulation strategies

### i. Eulerian Schemes (domain divided into evenly-distributed cells)

- **Finite Volume Method**
- **Collocated grid**: Stores all velocity components and pressure at the same grid points.
- **Staggered grid**: Stores velocity components at cell faces and pressure at cell centers, improving stability for incompressible flows.

### ii. Lagrangian Schemes (domain discretized into a set of particles)

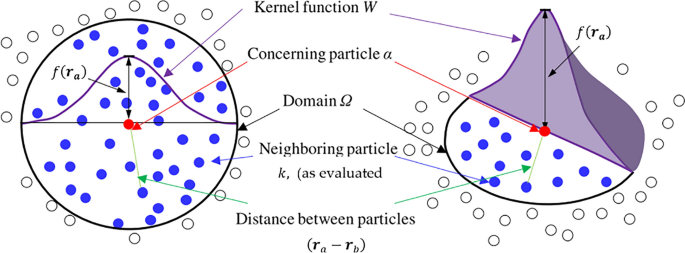
- **Smoothed Particle Hydrodynamics (SPH)**: A particle-based method for fluid simulation.

- **Position-Based Dynamics (PBD)**: Handles various physical phenomena including fluids, deformable solids, and cloth by directly manipulating particle positions instead of computing forces and accelerations.

### iii. Hybrid schemes

- **Particle-In-Cell (PIC)**: Basic hybrid particle–grid method combining Lagrangian particles and Eulerian grids.
- **Fluid Implicit Particle (FLIP) method**: Transfers momentum differences rather than absolute values, improving dynamic effects at the cost of some stability.
- **Material Point Method (MPM)**: Incorporates the deformation gradient along with momentum to capture solid–fluid interactions and elastic effects.
- **Affine Particle-In-Cell (APIC) method**: Uses affine velocity fields for particles, reducing numerical dissipation and improving stability.
- **Polynomial Particle-In-Cell (PolyPIC)**: Extends APIC by incorporating higher-order polynomial velocity fields for more accurate momentum transfer.
- **Moving Least Squares Material Point (MLS-MPM)**: Employs moving least squares for grid interpolation and differentiation, enhancing accuracy and robustness in simulations.

## 2. Advanced computational approaches

### i. Adaptive solutions

- **Temporal adaptivity**

- **Global time stepping**: Determing time step size by CFL condition as shown below, the $\lVert \mathbf{u}_c \rVert$ represents the speed of the information propagation, and the Courant number $C_{max}$ varies case by case.
$$ C \equiv \frac{\lVert \mathbf{u}_c \rVert \Delta t}{\Delta x} < C_{max}$$
- **Regional time stepping (Asynchronous time integration)**: Subdivides doamin into smaller regions using octrees, with independent time steps, aim for scenarios with both vigorous and calm regions exist.

- Spatial adaptivity (Multiscale)
- **Eulerian grids**: Uses an octree data structure for adaptive resolution.
- **Lagrangian methods**: Adjusts particle sampling via local merging or splitting to adaptively refine particle resolution.
- **Hybrid methods**: Combine Eulerian and Lagrangian adaptivity.
- **Particle splitting–collapsing scheme**: Adjust particle size in FLIP simulations based on distance to the fluid surface (larger particles further from the surface).
- **Hollow scheme**: Lagrangian representation for outer flow, Eulerian for inner flow.
- **Adaptive merge/split octree grids for FLIP**: Dynamically refine grid resolution where needed while maintaining coarser resolution elsewhere.

### ii. Parallelization

- **Single processing unit**

> [!Tip]
> Pure Eulerian and Lagrangian scheme can be readily parallelized. The hybrid methods is the pain in the ass due to the different nature of particles and grids.

- [**Voxel Data Block (VDB) method**](https://www.researchgate.net/publication/259288658_VDB_High-Resolution_Sparse_Volumes_with_Dynamic_Topology): Stores sparse volumetric data, resolves the parallel particle-to-grid rasteriza inherent in hybrid methods.
- [**Schur complement method**](https://dl.acm.org/doi/10.1145/3092818): Divides the simulation domain into subdomains with face edges and cross-points.
- [**New data-oriented programming language—Taichi**](https://www.taichi-lang.org/): Manipulate sparse data structures with a compiler designed to automatically optimize and parallelize code.

- **Multiple processing units (Multi-GPU)**

>[!Tip]
> Challenge lies in CPU-GPU data exchange.

- [**Schur complement method**](https://dl.acm.org/doi/10.1145/2980179.2982430): Partitions the simulation domain across multiple GPUs, with CPU coordinating interactions between regions.
- [**Restructured MPM algorithm**](https://sites.google.com/view/siggraph2020-multigpu): Redesigns particle data structures to enable coalesced memory access and avoid atomic operations during particle-to-grid transfers.
- [**Multi-kernel launch methodology**](https://arxiv.org/abs/2101.11856): Optimizes GPU kernel execution by managing multiple launches to reduce CPU–GPU synchronization overhead.

- **Distributed systems**
- [**Parallel data transfer driver**](https://pubmed.ncbi.nlm.nih.gov/22350196/): Enables efficient I/O for large-scale Hierarchical Data Format Version 5 (HDF5) datasets.
- [**Multi-core cloud computing**](https://dl.acm.org/doi/10.1145/3173551): Exploits parallelism across multiple CPU cores in cloud environments.
- [**Load-balancing scheme**](https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.13510?msockid=0c12b1d856696b5e19c0a40d52696d54): Dynamically distributes computational workload in sparse fluid simulations to reduce bottlenecks.
- [**Micro-partitioning**](https://onlinelibrary.wiley.com/doi/full/10.1111/cgf.13809?msockid=0c12b1d856696b5e19c0a40d52696d54): Subdivides simulation domains into fine-grained partitions to improve load balance and minimize communication overhead.

### iii. Data-driven approaches

> [!Tip]
> With parallelization, fluid simulation using traditional physical methods still requires high computational resources, specifically, on time steps for stability. Data-driven approaches provide an alternative solution for real-time interactive fluid simulation.

- **Model reduction**
- [**Galerkin projection**](https://dl.acm.org/doi/10.1145/1141911.1141962): Precompute a low-dimensional basis for fluid dynamics and project the high-dimensional fluid equations onto this reduced space.

- **Machine learning**
- [**Convolutional Neural Networks (CNN)**](https://ieeexplore.ieee.org/document/8478400): Introduced to learn mappings for fluid dynamics, e.g., predicting velocity or pressure fields from previous states.
- [**Artificial Neural Networks(ANN)**](https://onlinelibrary.wiley.com/doi/abs/10.1111/cgf.14010?af=R&msockid=0c12b1d856696b5e19c0a40d52696d54): Applied to approximate the pressure projection step in incompressible fluid simulations.
- [**ScalarFlow**](https://arxiv.org/abs/2011.10284): The first large-scale volumetric dataset for real smoke reconstruction using computer graphics and machine learning.