# HW15 - Q3 ###### tags: `演算法`, `109-2` ## Question **Exercises 34.5-1** The subgraph-isomorphism problem takes two undirected graphs G1 and G2, and it asks whether G1 is isomorphic to a subgraph of G2. Show that the subgraph-isomorphism problem is NP-complete ## Mein Answer ### 什麼是 Subgraph-Isomorphism Problem 這個問題是要我們找到在 G2 的圖裡面，有沒有存在 G1 的圖 ，稱 G ； 反過來說也就是 G1 有沒有射在 G2 上，射在 G 點。 上個圖可以比較了解： ![](https://i.imgur.com/RILY5sf.png) ![](https://media.geeksforgeeks.org/wp-content/uploads/20200613013913/abc4.jpg) 你不覺得 Isomorphism 念起來很有魔性？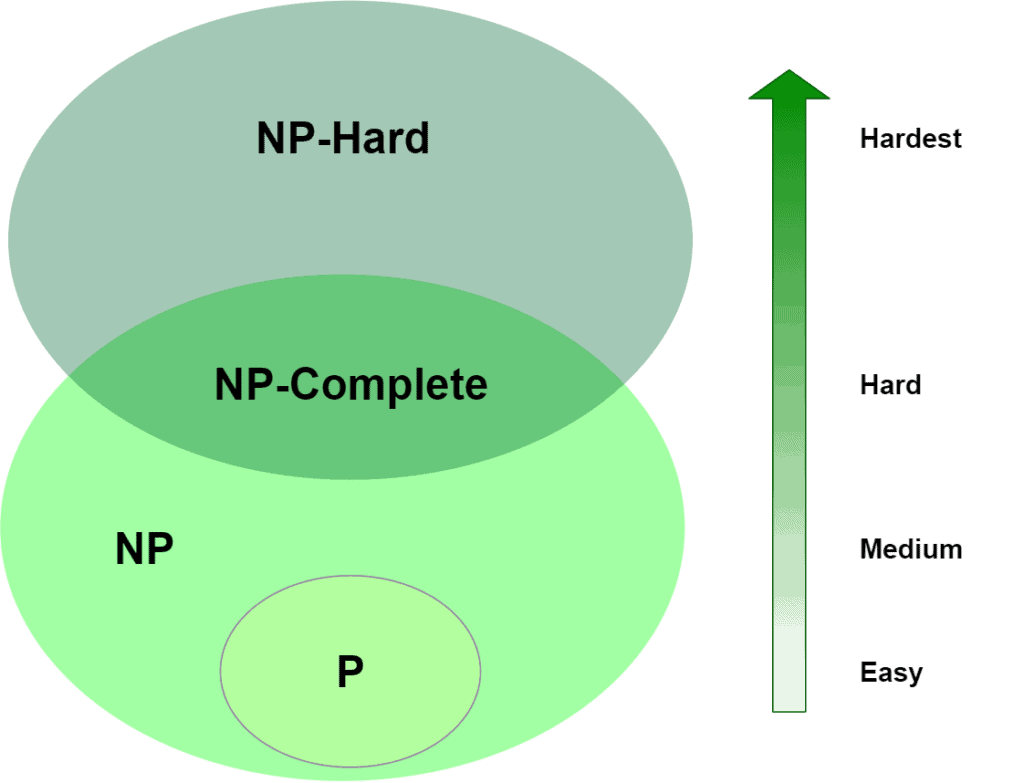就叫他 *愛搜魔菲森* 好了 ### 不證自明...還是得證明 如果某個問題是 NP-Complete，那他就會是 NP 也是 NP-Hard ![](https://www.baeldung.com/wp-content/uploads/sites/4/2020/03/P-NP-NP_Hard-NP-Complete-1-1-1024x783.png) 所以我們現在要做的事似是試試證明這個愛搜魔菲森是 NP 也是 NP-Hard <!-- The Subgraph Isomorphism Problem belongs to NP – If a problem belongs to the NP class, then it should have polynomial-time verifiability. Given a certificate, we should be able to verify in polynomial time if it is a solution to the problem. --> #### *愛搜魔菲森* 是 NP > NP: 驗證結果的時間為 Polynomial 以下 這題 NP 的驗證很簡單 要是我們已經拿到了 G1、G2 跟 G ，那我們只需要遞迴過 G 的點是不是和 G1 相同，只需要線性時間，所以的確是 NP。 <!-- Certificate: Let G be a subgraph of G2. We also know the mapping between the vertices of G1 and G. Verification: We have to check if G1 is isomorphic to G or not. (i) Checking if the mapping is a bijection and (ii) Verifying if, for every edge (u, v) in G1, there is an edge (f(u), f(v)) present in G takes polynomial time. Therefore, the Subgraph Isomorphism Problem has polynomial time verifiability and belongs to the NP class. --> <!-- To do this, first, notice that it is in NP, where the certificate is just the injection from G1 into G2 so that G1 is isomorphic to its image. --> #### *愛搜魔菲森* 是 NP-HARD > NP-Hard: 想辦法把問題 reduce 成其他 NP-Hard 或 NP-Complete 問題 =>$\forall Y \in NP, Y \le_p X$ 我們拿 NP-Complete 的 [分團問題](https://zh.wikipedia.org/wiki/%E5%88%86%E5%9C%98%E5%95%8F%E9%A1%8C) 來當底 假設分團問題中，圖 $G$ 存在 $k$ 個點可以構成團 (clique)，並且我們有一個演算法 $A$ 可以在 polynomial-time 內解出來。 那麼我們把這個圖 $G$ 和 $k$ 分別當作 *愛搜魔菲森* 的 $G_2$ 和 $G_1$，這樣我們也可以在 polynomial-time 解出 *愛搜魔菲森* 了...嗎？ ![](https://i.imgur.com/TF4xXyg.png) > 分團問題：1-2-5 是 k (他們完全相連)； > 我們把 k 當作 *愛搜魔菲森* 的 G1，整張圖 G 就是 G2：看啊！G1 射進 G2 了 很可惜的，前面提過分團問題是 NP-Complete，所以沒有 polynomial-time 的演算法，因此 *愛搜魔菲森* 是 NP-Hard 確認。 ![](https://i.imgur.com/sAGe2y7.png) <!-- Now, to see that it is NP complete, we will do a reduction to clique. That is, to detect if a graph has a clique of size k, just let G1 be a complete graph on k vertices and let G2 be the original graph. If we could solve the subgraph isomorphism problem quickly, this would allow us to solve the clique problem quickly. --> ### References - [Ciaran Mccreesh, Patrick Prosser, Christine Solnon, James Trimble. When Subgraph Isomorphism is Really Hard, and Why This Matters for Graph Databases. Journal of Artificial Intelligence Research, Association for the Advancement of Artificial Intelligence, 2018, 61, pp.723 - 759. ff10.1613/jair.5768ff. ffhal-01741928](https://hal.archives-ouvertes.fr/hal-01741928/document) - [P, NP, NP-Complete and NP-Hard Problems in Computer Science baeldungCS](https://www.baeldung.com/cs/p-np-np-complete-np-hard) - [How to Prove That a Problem Is NP-Complete? - baeldungCS](https://www.baeldung.com/cs/prove-np-complete) - [Proof that Subgraph Isomorphism problem is NP-Complete Difficulty Level : Expert - GeeksForGeeks](https://www.geeksforgeeks.org/proof-that-subgraph-isomorphism-problem-is-np-complete/)