# 2020年8月11日 靜磁學
###### tags: `高中物理`
## 第一階段:隨機抽問
1. (簡答題)請說明必歐-沙伐定律(Biot–Savart law)的內容。
2. (計算題)兩條平行、固定且電流方向相同之載流導線,長度均為 $5~\text{m}$,相距 $2~\text{mm}$,其中一條電流強度為 $3~\text{A}$,一條電流強度為 $4~\text{A}$,請問兩條導線之間的作用力量值為何?是互相吸引還是互相排斥?
3. (是非題)磁場線上某一點的切線方向平行於某一質點在那一點所受的磁力方向。
4. (簡答題)請解釋何謂「磁場的環場積」。
5. (證明題)請證明帶電質點在均勻、穩定磁場中運動的軌跡是螺旋線(helix),並計算出螺距(pitch)。
6. (證明題)載流圓形線圈在軸向上的磁場量值為 $$B=\dfrac{\mu_0Ia^2}{2(a^2+x^2)^{3/2}},$$ 其中 $I$ 為電流強度,$a$ 為線圈半徑,$x$ 為軸上的點到線圈圓心的距離。*提示:* 利用下圖
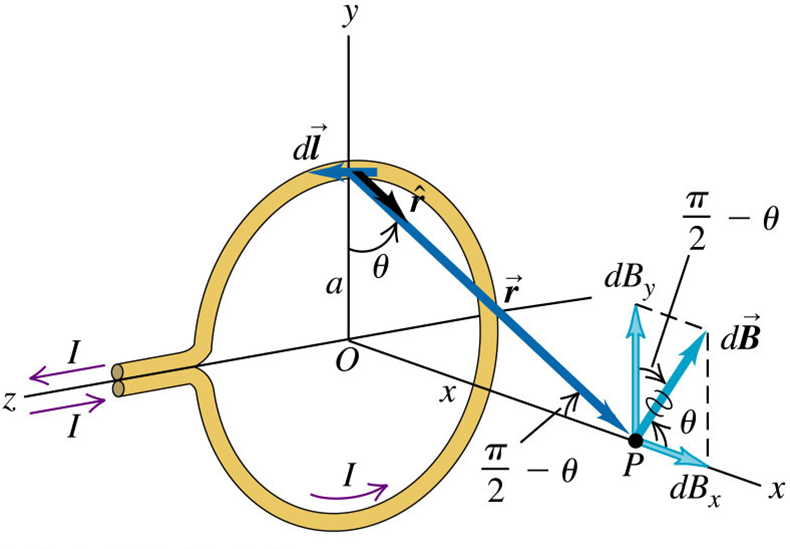
圖片來源:[Miniphysics](https://www.miniphysics.com/uy1-magnetic-field-of-a-circular-current-loop.html)
7. (簡答題)請說明速度選擇器的原理。
8. (計算題)下圖是磁軌砲(railgun)的簡圖。

假設軌道長 $10~\text{m}$,拋射物質量 $1~\text{kg}$、長度 $10~\text{cm}$;又控制外加磁場量值 $10~\text{T}$,在兩軌道之間均勻且穩定,請問要通入的脈衝電流強度至少要多大,才能使拋射物從靜止加速離開軌道時,速率達到 $1~\text{km/s}$。不計摩擦力、空氣阻力,也不考慮電磁感應。
9. (簡答題)有一條載流長直導線 $L_1$ 放置在空間中的 $x$ 軸上,電流方向為 $+x$,又有一條載流長直導線 $L_2$ 放置在直線 $\{(x,y,z)|x=0,z=1\}$ 上,電流方向為 $+y$。請描述 $L_1$ 所受的力或力矩方向。
10. (簡答題)請說明載流線圈在均勻磁場中所受力矩。
### 答題狀況
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| +2 | +1 | +0 | +1 | +2 | +2 | +2 | +0 | +0 | +1 |
## 第二階段:
### 一、安培環路定律(補充)
> 安培環路定律(Ampère's circuital law)表明,「磁場沿著環繞載流導線的閉合迴路的路徑積分」 正比於「導線所載的電流」,比例常數就是真空中的磁導率。
用數學式表達,就是$$\oint_C\mathbf{B}\boldsymbol\cdot\text{d}\boldsymbol\ell=\mu_0 I_{enc},\tag{1}$$
其中 $C$ 是環繞著導線的閉合迴路,$\mathbf{B}$ 是磁場,$\text{d}\boldsymbol\ell$ 是 $C$ 上面的微小線元素向量,$I_{enc}$ 是導線上的電流(被 $C$ 圍住)。
環場積分的意義如下圖所示:

根據向量微積分中的斯托克斯定理,(1) 式可以改寫成更簡潔的形式:$$\boldsymbol\nabla\boldsymbol\times \mathbf{B}=\mu_0\mathbf{J},\tag{2}$$ 其中 $\mathbf{J}$ 是電流密度
原版安培環路定律只適用於靜磁學,也就是電流 $I_{enc}$ 與 $\mathbf{B}$ 都不隨時間而變。
1861年,馬克士威推論出含時電場會生成磁場,因此他引入了電位移的觀念,修正了 (1)、(2) 式,成為馬克士威方程組的其中一條方程式。
### 二、物理量
#### 1. 磁力(符號:++  ++)
- 〔純量/向量〕
- 定義:
磁體(能產生磁場的物體)間的相互作用,它通常指的是
1. ++    ++ 的磁部分,也有可能是指
2. ++    ++ 在 ++   ++ 中所受的力、
3. 兩平行 ++    ++ 之間的作用力—— ++  ++ 力。
- 單位:
#### 2. 磁場(符號:++  ++)
- 〔純量/向量〕
- 定義
- 概念化:++   ++ 密度——單位體積內的「淨」++   ++ 數量
- 單位
- SI制:
- 來源
- 電流(填線圈或導線類型)
- ++    ++,例如:$\boxed{B=\dfrac{\mu_0I}{2\pi s}}$
- ++    ++,例如:$\boxed{B=\dfrac{\mu_0I}{2R}}$
- ++    ++:$\boxed{B=\mu_0 nI}$
- 亥姆霍茲線圈:$B=\left(\dfrac{4}{5}\right)^{3/2}\dfrac{\mu_0 nI}{R}$
- (寫出其他三個來源)
### 三、重要定律、方程式、公式
#### 1. 必歐-沙伐定律
設定一段固定於原點 $O$ 的載流微小線元素,其作用於一點 $\mathbf{r}$ 的微小磁場 $d\mathbf{B}$ 滿足$$\boxed{d\mathbf{B}=\color{white}{\dfrac{\mu_0}{4\pi}\dfrac{Id\boldsymbol\ell\times \hat{\mathbf{r}}}{r^2}}},$$其中:
- $I$ 為通過 ++     ++ 的電流強度,
- $d\boldsymbol\ell$ 是 ++     ++ 向量,其方向為 ++  ++ 方向,
- $\hat{\mathbf{r}}$ 為 向量 $\mathbf{r}$ 的 ++    ++,
- $r$ 為 向量 $\mathbf{r}$ 的 ++  ++。
純量形式為$$\boxed{dB=\color{white}{\dfrac{\mu_0}{4\pi}\dfrac{Id\ell \sin\theta}{r^2}}}。$$
必歐-沙伐定律有兩個延伸定律。
1. 安培力定律
設定兩條 ++  ++ 、 ++   ++ 、 ++    ++ 的載流導線,則在自由空間內,任意一條導線施加於對方的「++        ++」 $f_m$ 為$$\boxed{f_m=\color{white}{\dfrac{\mu_0I_1I_2}{2\pi r}}},$$其中:
- $I_1$、$I_2$ 分別是載於兩導線的電流強度,
- $r$ 是兩條導線之間的 ++    ++ 。
當電流方向相同,安培力為〔吸引/排斥〕力;
當電流方向相反,安培力為〔吸引/排斥〕力。
2. 安培環路定律(高中未提及形式,但有以下應用。)
1. **載流長直導線**在 ++      ++ 的磁場量值為$$\boxed{B=\color{white}{\dfrac{\mu_0I}{2\pi s}}},$$其中:
- $I$ 為電流強度,電流方向是安培右手定則中 ++  ++ 的方向,
- $s$ 為 ++    ++,
- 磁場方向就是安培右手定則中 ++  ++ 的方向。
2. **載流圓形線圈**在 ++  ++ 的磁場量值為$$\boxed{B=\color{white}{\dfrac{\mu_0I}{2R}}},$$其中:
- $I$ 為電流強度,電流方向是安培右手定則中 ++  ++ 的方向,
- $R$ 為 ++    ++,
- 磁場方向就是安培右手定則中 ++  ++ 的方向。
3. **載流圓形線圈**在軸向上的磁場量值為$$\boxed{B=\color{white}{\dfrac{\mu_0IR^2}{2(R^2+z^2)^{3/2}}}},$$其中:
- $I$ 為電流強度,電流方向是安培右手定則中 ++  ++ 的方向,
- $R$ 為 ++    ++,
- $z$ 為 ++    ++ 到 ++    ++ 的距離,
- 磁場方向就是安培右手定則中 ++  ++ 的方向。 
4. **螺線管**在 ++  ++ 造成的磁場量值為$$\boxed{B=\color{white}{\mu_0 nI}},$$其中:
- $I$ 為電流強度,電流方向是安培右手定則中 ++  ++ 的方向,
- $n$ 為 ++        ++。
- 磁場方向就是安培右手定則中 ++  ++ 的方向。

注意:(1) 在螺線管管口會有 ++  ++ 效應,所以上式只是用離管口較遠的 ++  ++。(2) 在管口的磁場量值為 $\boxed{B=\color{white}{\mu_0 nI/2}}$。
#### 2. 勞倫茲力
運動於電磁場中、帶有電量 $q$ 的點電荷,其受力為$$\boxed{\color{white}{\mathbf{F}=q(\mathbf{E}+\mathbf{v}\times\mathbf{B})}},$$其中:
- $\mathbf{v}$ 電荷運動的 ++  ++,
- $\mathbf{E}$ 為 ++    ++,
- $\mathbf{B}$ 為 ++  ++。
## 第三階段:解答課前提問
### p.211 精選例題4 附註討論(1)
令 $I_j$ 在 $A$ 點造成的磁場為 $\mathbf{B}_j$ ,用右手定則判斷磁場的方向為 $\hat{\mathbf{e}}_j$ $(j=1,2,3,4)$。判斷如下:$$\hat{\mathbf{e}}_1=-\hat{\mathbf{e}}_x,\quad \hat{\mathbf{e}}_2=-\hat{\mathbf{e}}_y,\quad \hat{\mathbf{e}}_3=+\hat{\mathbf{e}}_x,\quad \hat{\mathbf{e}}_4=+\hat{\mathbf{e}}_x$$
$\displaystyle\begin{align}\mathbf{B}&=\sum_j\mathbf{B}_j=\sum_j\dfrac{\mu_0 I_j}{2\pi r}\hat{\mathbf{e}}_j=\dfrac{\mu_0}{2\pi r}\sum_jI_j\hat{\mathbf{e}}_j\\&=\dfrac{4\pi\times 10^{-7}~\text{T-m/A}}{2\pi\times(2\times 10^{-2}~\text{m})}\left[(10~\text{A})(-\hat{\mathbf{e}}_y)+(20~\text{A})(-\hat{\mathbf{e}}_y)+(20~\text{A})(\hat{\mathbf{e}}_x)+(10~\text{A})(\hat{\mathbf{e}}_x))\right]\\&=(10^{-5}~\text{T})\left(30\hat{\mathbf{e}}_x-30\hat{\mathbf{e}}_y\right)=(3\times10^{-4}~\text{T})\hat{\mathbf{e}}_x-(3\times10^{-4}~\text{T})\hat{\mathbf{e}}_y\end{align}$
$B=|\mathbf{B}|=3\sqrt{2}\times10^{-4}~\text{T}$
### p.240 精選例題10
#### 解法3
磁偶極矩 $\boldsymbol\mu$ 在磁場中 $\mathbf{B}$ 所受力矩為 $\boldsymbol\tau=\boldsymbol\mu\boldsymbol\times\mathbf{B}$
一個載流迴路可以視為磁偶極子,其磁偶極矩 $\boldsymbol\mu=I\mathbf{a}$,其中 $I$ 為所載電流、$\mathbf{a}$ 為面積向量(右手定則:四指為電流方向,拇指為面積向量方向。)
圖中磁偶極矩穿出紙面($+z$ 方向)、磁場向右($+x$ 方向),故力矩向上($+y$ 方向),故線圈右側(三角形$ACM$)穿入紙面,線圈左側(三角形$ABM$)穿出紙面,選(A)。
### p.276 精選例題24
答案更正為BCD
### p.281 精選例題30
張鎮麟:「運動的獨立性」——不完全正確。
$\mathbf{v}=v_x\hat{\mathbf{e}}_x+v_y\hat{\mathbf{e}}_y$、$\mathbf{B}=-B{\mathbf{e}}_z$
$\mathbf{F}=q\mathbf{v}\boldsymbol\times\mathbf{B}=q(v_x\hat{\mathbf{e}}_x+v_y\hat{\mathbf{e}}_y)\boldsymbol\times(-B{\mathbf{e}}_z)=q\begin{vmatrix}\hat{\mathbf{e}}_x&\hat{\mathbf{e}}_y&\hat{\mathbf{e}}_z\\v_x&v_y&0\\0&0&-B\end{vmatrix}=-qv_yB\hat{\mathbf{e}}_x+qv_xB\hat{\mathbf{e}}_y$
令 $\omega=\dfrac{qB}{m}$,
三個區域的運動方程式:[^1]
1. 區域I:$z<0$ $$\left.\begin{array}{l}F_x=-qv_yB=ma_x\\F_y=qv_xB=ma_y\\F_z=0=ma_z\end{array}\right\}\implies\left.\begin{array}{l}v_x(t)=v_{0x}\sin{\omega t}+v_{0y}\cos{\omega t}\\v_y(t)=v_{0x}\cos{\omega t}-v_{0y}\sin{\omega t}\\v_z(t)=v_{0z}\end{array}\right\}$$
2. 區域II:$0<z<\ell$ $$\left.\begin{array}{l}F_x=-qv_yB=ma_x\\F_y=qv_xB=ma_y\\F_z=qE=ma_z\end{array}\right\}\implies\left.\begin{array}{l}v_x(t')=v_{1x}\sin{\omega t'}+v_{1y}\cos{\omega t'}\\v_y(t')=v_{1x}\cos{\omega t'}-v_{1y}\sin{\omega t'}\\v_z(t')=v_{1z}+\frac{qE}{m}t'\end{array}\right\}$$
3. 區域III:$z>\ell$ $$\left.\begin{array}{l}F_x=-qv_yB=ma_x\\F_y=qv_xB=ma_y\\F_z=0=ma_z\end{array}\right\}\implies\left.\begin{array}{l}v_x(t'')=v_{2x}\sin{\omega t''}+v_{2y}\cos{\omega t''}\\v_y(t'')=v_{2x}\cos{\omega t''}-v_{2y}\sin{\omega t''}\\v_z(t'')=v_{2z}\end{array}\right\}$$
有幾點注意:
- 可以再將速度的函數對時間積分、搭配初始條件,得到位置的函數,就可證明在區域I、III的軌跡是螺旋,區域II為非等距螺旋。
- $t'$ 和 $t''$ 分別是從進入區域II、III的瞬間開始計時。
- $v_{jx}$ $(j=0,1,2)$ 之間是彼此相關的, $v_{jy}$ $(j=0,1,2)$ 之間也是彼此相關的。
- $v_{0z}=v_{1z}$,此外,$v_{1z}$ 透過 $\ell$ 而與 $v_{2z}$ 有關。
### p.283 精選例題32
答案更正為BD
[^1]: 這裡 $x$ 和 $y$ 的運動方程式有一個耦合的微分方程組:$$\left.\begin{array}{l}\ddot{x}=-\omega\dot{y}\\\ddot{y}=\omega\dot{x}\end{array}\right\},$$ 變數上的點代表對時間的導數。把方程組的第二式代入第一式,會得到 $\dddot{x}=-\omega^2\dot{x}$,這可以解得$$\dot{x}=\alpha_0\sin{\omega t}+\beta_0\cos{\omega t},$$ 再將此代入方程組,可解得$$\dot{y}=\alpha_0\cos{\omega t}-\beta_0\sin{\omega t}。$$
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet