基礎排序 - HackMD

# 基礎排序 by 南天門日月卦長 --- ## 預備知識 1. 陣列 2. 迴圈 3. 函數 4. 時間複雜度 ---- ## 你知道這些代表神麼意思嗎? ``` cpp= int s[] = {7,1,2,2,9,4,8,7}; int a[10000005] = {1}; //想清楚！！ int b = s[8]; //b是什麼呢？ ``` ---- ## 你知道這些代表神麼意思嗎? ``` cpp= int s[] = {7,1,2,2,9,4,8,7}; int b=0; for(int i=0;i<8;++i) b += s[i]; for(;b--;){ cout<<7122<<'\n'; } ``` ---- ## 這個函數的時間複雜度? ``` cpp= int MAX(int s[], int n){ int res = s[0]; for(int i=1;i<n;++i) if(s[i]>res) res = s[i]; return res; } ``` ---- ## 常見的時間複雜度 * 找n個數裡的最大值？ * 掃過所有數字選出最大的 $\longrightarrow \mathcal{O}(n)$ * 判斷一個數字n是不是質數？ * 掃過 $2\sim n \longrightarrow \mathcal{O}(n)$ * 掃過 $2\sim \sqrt{n} \longrightarrow \mathcal{O}(\sqrt{n})$ --- ## 交換兩變數在接下來的課程中我們會經常需要交換兩變數的值因此我們先來複習一下 ---- ## 交換兩變數 ``` cpp= int a = 7122, b = 9487; //交換a,b int tmd = a; a = b; b = tmd; cout << a << ' ' <``` 可以用更簡單的寫法交換兩個變數更詳細用法會在之後STL的課程告訴你 ---- ## 交換兩變數 ``` cpp= #include<iostream> #include<algorithm> int main(){ int a = 7122, b = 9487; //交換a,b std::swap(a,b); std::cout << a << ' ' < #include<algorithm> using namespace std; //這樣可以省略 std:: int main(){ int a = 7122, b = 9487; //交換a,b swap(a,b); cout << a << ' ' <將s前8項排序---> s[0]~s[7]分別為1, 1, 2, 2, 2, 2, 7, 7 ---  ## 基於交換的排序 --- ## 基本想法對於一個排序好長度為n的陣列s 對於任何的 0 $<$ i $<$ n 一定滿足 s[i] $\ge$ s[i-1] ---- 所以說如果我發現 s[i] < s[i-1] 那就表示s是沒有排序好的 ---- 這個性質可以幫助我們在$\mathcal O (n)$的時間判斷陣列有沒有按順序排 ``` cpp= bool sorted(int s[],int n){ for(int i=1;i<n;++i) if(s[i]<s[i-1]) return false; return true; } ``` ---  ## very stupid sort 超級蠢的排序 --- 既然只要存在 s[i] < s[i-1] 就是沒有排序好 ---- 那我們就在陣列裡面一直找 s[i] < s[i-1] 只要遇到了就把 s[i], s[i-1]做交換就行啦！ ---- 一直找直到陣列裡面沒有 s[i] < s[i-1] 為止 ---- ## 讓我們來看程式碼 ``` cpp= void veryStupidSort(int s[], int n){ while(!sorted(s,n)){ for(int i=1; i<n; ++i){ if(s[i]<s[i-1]){ swap(s[i],s[i-1]); break; } } } } ``` ---- ## 更好的寫法 ``` cpp= void veryStupidSort(int s[], int n){ for(int i=1; i<n; ++i){ if(s[i]<s[i-1]){ swap(s[i],s[i-1]); i = 0; //注意等一下會++i } } } ``` ---- ## 蠢在哪裡？ ---- ## 時間複雜度不要以為只有一個for時間複雜度就是$\mathcal O(n)$喔 ---- 仔細看每次發現 s[i] < s[i-1] 就會把 i 歸 0 意思是每次交換後會重新掃描陣列一次！ ---- 重新掃描陣列大約花$\mathcal O(n)$的時間因此總複雜度是： $\mathcal O(n)\times$交換次數 ---- ## 交換次數稍微思考一下會發現在陣列「倒著排序」的情況下需要最多的交換次數 ``` cpp= int s[]={5,4,3,2,1}; ``` ---- 仔細算會發現對長度n「倒著排序」的陣列來說用我們的排序法需要進行 $(n-1)(n-2)/2=\mathcal O(n^2)$次交換 ---- ## 總複雜度因此我們演算法的複雜度是$\mathcal O(n) \times \mathcal O(n^2)=\mathcal O(n^3)$ ---- 但是排序最快可以做到$\mathcal O(n \;log \;n)$，這方法太蠢了 ---  ## bubble sort 氣泡排序 --- 剛剛的第一份code裡面有一個break ``` cpp= void veryStupidSort(int s[], int n){ while(!sorted(s,n)){ for(int i=1; i<n; ++i){ if(s[i]<s[i-1]){ swap(s[i],s[i-1]); break;//拿掉會發生什麼事呢? } } } } ``` ---- 拿掉break就變成所謂的bubble sort了 ``` cpp= void bubbleSort(int s[], int n){ while(!sorted(s,n)){ for(int i=1; i<n; ++i){ if(s[i]<s[i-1]) swap(s[i],s[i-1]); } } } ``` ---- ## 複雜度有變好嗎？ ---- 當然有！變$\mathcal O(n^2)$ 我們現在要來證明外層的while最多只會執行n次！ ---- 我們要來證明，不管陣列的元素排列順序執行一次底下這個程式碼之後最大的元素一定會被放在s[n-1]的位置！ ```cpp= for(int i=1; i<n; ++i){ if(s[i]<s[i-1]) swap(s[i],s[i-1]); } ``` ----  * 假設陣列長這樣 * 當前i=2 * 此時s[i-1]為最大值(99) | | i-1 | i | | | | ---- | ---- | ---- | ---- | ---- | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 99 | 71 | 22 | 87 | ----  * 因為 s[i]<s[i-1] * 所以會執行swap的操作 * 執行完後會得到以下的結果 | | i-1 | i | | | | ---- | ---- | ---- | ---- | ---- | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 99 | 22 | 87 | ----  * 接著會執行for的++i * 執行完後會得到以下的結果 * 你會發現現在s[i-1]又變成最大值了(99) | | | i-1 | i | | | ---- | ---- | ---- | ---- | ---- | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 99 | 22 | 87 | ----  * 最大值一定比其他所有元素大，如此不斷重複 * 直到i==n-1為止 * 你會發現最後最大值就會跑到s[n-1]的位置 | | | i-1 | i | | | ---- | ---- | ---- | ---- | ---- | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 22 | 99 | 87 | ----  * 最大值一定比其他所有元素大，如此不斷重複 * 直到i==n-1為止 * 你會發現最後最大值就會跑到s[n-1]的位置 | | | | i-1 | i | | ---- | ---- | ---- | ---- | ---- | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 22 | 99 | 87 | ----  * 最大值一定比其他所有元素大，如此不斷重複 * 直到i==n-1為止 * 你會發現最後最大值就會跑到s[n-1]的位置 | | | | i-1 | i | | ---- | ---- | ---- | ---- | ---- | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 22 | 87 | 99 | ---- 只要最大值在某個 i-1 的位置他最後一定會被交換到 s[n-1] 去 ---- 除非最大值本身就在 s[n-1] 否則他一定會在某個 i-1 的位置因此執行一次for之後最大值一定會被放到s[n-1] ---- 那如果最大值已經在 s[n-1]了執行for迴圈之後會發生什麼事呢？ ---- 稍微想一下你會發現第2大值就一定會被放在s[n-2]的位置 ---- 準確來說執行第k次for迴圈後第k大值就會被放在s[n-k]的位置 (這也是被稱為bubble sort的原因) ---- 因此最多只要執行n-1次迴圈就可以完成排序故總複雜度為$\mathcal O(n(n-1))=\mathcal O(n^2)$ ---- 因為已經知道最多只會執行n-1次while 可以把code寫得更短 ```cpp= void bubbleSort(int s[], int n){ for(int t=0; t<n-1; ++t) for(int i=1; i<n-t; ++i) if(s[i]<s[i-1]) swap(s[i],s[i-1]); } ``` ---  ## selection sort 選擇排序 --- ## 基本想法把最小的元素找出來，和s[0]交換位置接著找第二小的，和s[1]交換位置接著找第三小的... 最後所有s[0]~s[n-1]都會是排序好的 ---- 再找第k小的元素時由於前k-1小的元素都已經被放在s[0]~s[k-2]了故s[k-1]~s[n-1]中最小元素就是原本陣列中的第k小 ---- ## 從s[k]~s[n-1]中找最小的index ```cpp= int find_index_of_min_element(int s[],int k,int n){ int res = k++; for(; k<n; ++k) if(s[k]<s[res]) res = k; return res; } ``` ---- ## selection sort ```cpp= void selectionSort(int s[],int n){ for(int i=0; i<n; ++i){ int min_id = find_index_of_min_element(s,i,n); swap(s[i],s[min_id]); } } ``` ---- ## 複雜度顯然 find_index_of_min_element 是$\mathcal O(n)$ 總共會執行$n$次故總複雜度為$n \times \mathcal O(n)=\mathcal O(n^2)$ ---- ## 只用一個函數的寫法 ```cpp= void selectionSort(int s[],int n){ for(int i=0; i<n; ++i){ int min_id=i; for(int j=i+1; j<n; ++j) if(s[j]<s[min_id]) min_id = j; swap(s[i],s[min_id]); } } ``` ---- ## 補充可以利用一種叫做[Heap](https://en.wikipedia.org/wiki/Heap_(data_structure))的資料結構幫陣列做預處理這樣的話 find_index_of_min_element 就可以做到$\mathcal O(log\;n)$ 總複雜度就會是$\mathcal O(n \;log\;n)$，稱為[heap sort](https://en.wikipedia.org/wiki/Heapsort) ---  ## insertion sort 插入排序 --- ## 基本想法 1. 把陣列分成排序好(左半)和沒有排序好(右半) 2. 將(右半)的最左邊元素加入(左半)中 3. (左半)的部分一直向左邊比，如果順序不對就交換 4. 重複2,3直到排序完成 ---- ## 下一步會發生什麼事呢？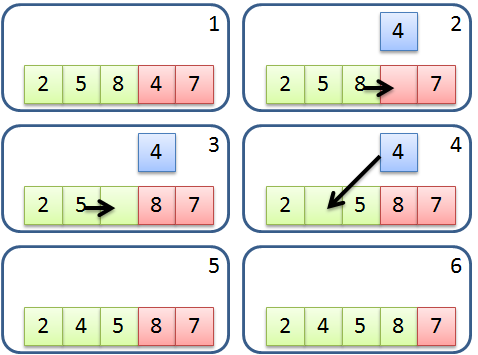 ![插入排序](https://s3.amazonaws.com/media-p.slid.es/uploads/501803/images/2561881/1352639756-2821685118.png) ---- ## 很短的code ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | i | | | | | ---- | ---- | ---- | ---- | ---- | | j-1 | j | | | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 99 | 22 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | i | | | | ---- | ---- | ---- | ---- | ---- | | | j-1 | j | | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 99 | 22 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | i | | | ---- | ---- | ---- | ---- | ---- | | | | j-1 | j | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 99 | 22 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | i | | | ---- | ---- | ---- | ---- | ---- | | | | j-1 | j | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 22 | 99 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | i | | | ---- | ---- | ---- | ---- | ---- | | | j-1 | j | | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 71 | 22 | 99 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | i | | | ---- | ---- | ---- | ---- | ---- | | | j-1 | j | | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 22 | 71 | 99 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | i | | | ---- | ---- | ---- | ---- | ---- | | j-1 | j | | | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 50 | 22 | 71 | 99 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | i | | | ---- | ---- | ---- | ---- | ---- | | j-1 | j | | | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 22 | 50 | 71 | 99 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | i | | | ---- | ---- | ---- | ---- | ---- | | j | | | | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 22 | 50 | 71 | 99 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | | i | | ---- | ---- | ---- | ---- | ---- | | | | | j-1 | j | | s[0] | s[1] | s[2] | s[3] | s[4] | | 22 | 50 | 71 | 99 | 87 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | | i | | ---- | ---- | ---- | ---- | ---- | | | | | j-1 | j | | s[0] | s[1] | s[2] | s[3] | s[4] | | 22 | 50 | 71 | 87 | 99 | ---- ## 模擬操作  ```cpp= void insertionSort(int s[],int n){ for(int i=1; i<n; ++i)// 小於i的都是已經排序好的(左半) for(int j=i; j && s[j]<s[j-1]; --j) swap(s[j],s[j-1]); } ``` | | | | | i | | ---- | ---- | ---- | ---- | ---- | | | | j-1 | j | | | s[0] | s[1] | s[2] | s[3] | s[4] | | 22 | 50 | 71 | 87 | 99 | ---- ## 複雜度分析顯然裡面的for是$\mathcal O(n)$ 而且每執行一次，(左半)的元素就會增加一個 ---- ## 複雜度分析因此裡面的for最多執行$n$次就排好序了故總複雜度是$n\times \mathcal O(n)=\mathcal O(n^2)$ ---- ## 好處 1. 常數很小 2. 當陣列很接近排序完成的情況會花比較少的時間$\simeq \mathcal O(n)$ 3. 當n很小( <= 15 )的時候在一般電腦上是跑最快的排序(我自己測的) ---  ## 其他有趣的排序 --- ## gnome sort 侏儒排序 ---- 其實就是insertion sort只用一個迴圈的寫法但是常數比較大仔細一看有點像 very stupid sort ```cpp= void gnomeSort(int s[], int n){ for(int i=0; i<n; ++i){ if(i && s[i]<s[i-1]){ swap(s[i],s[i-1]); i -= 2; } } } ``` ---- ## 複雜度和insertion sort一樣$\mathcal O(n^2)$ --- ## stooge sort 臭皮匠排序 ---- 取名來自於三個臭皮匠是我看過最優美的排序方法不用任何迴圈 ```cpp= void stoogeSort(int s[], int L, int R){ if(s[R]<s[L]) swap(s[L],s[R]); if(R-L<=1) return; int p = (R-L+1) / 3; stoogeSort(s, L, R-p); stoogeSort(s, L+p, R); stoogeSort(s, L, R-p); } ``` ---- ## 使用方法假設你要對長度為n的陣列s做排序 ```cpp= stoogeSort(s,0,n-1); ``` ---- ## 複雜度 * 遞推關係式 * $T(n) = 3T(\frac{2}{3}n)+\mathcal O(1)$ * by [master theorem](https://en.wikipedia.org/wiki/Master_theorem_(analysis_of_algorithms)), $T(n) = \mathcal O(n^{log_{1.5}3})=\mathcal O(n^{log 3/log 1.5}) \simeq \mathcal O(n^{2.71})$ ---  ## 補充 - 高效的排序法以下的排序法都是$\mathcal O(n\;log\;n)$ * [merge sort](https://en.wikipedia.org/wiki/Merge_sort) * [heap sort](https://en.wikipedia.org/wiki/Heapsort) * [introsort](https://en.wikipedia.org/wiki/Introsort)([quick sort](https://en.wikipedia.org/wiki/Quicksort)改良版) --- ## 有趣的影片 {%youtube kPRA0W1kECg %}