# 排序
> 上一篇文章　[時間複雜度](https://hackmd.io/@iDoNotWantToCoding/SJosmXioJl)
> 下一篇文章　[前綴合](https://hackmd.io/@iDoNotWantToCoding/S1vxNmsoJe)
> 先備知識　　無
> 延伸閱讀　　[基于比较排序的时间复杂度的下界](https://blog.csdn.net/qq_38206090/article/details/82381648)
---

## <font size = 6>前言</font>
混亂的房間，看起來九分甚至十分的惱人:hot_face: !想像你在看《鬼滅之刃:無限發…不對，列車篇》時，看到大哥被猗窩座貫穿的那一刻，哭的通哭流涕，想找衛生紙卻找不到，只好用衣服擦，結果被媽媽罵。在混亂不堪的房間找東西很困難，你必須要一個一個去找。

同樣的道理，從一個沒有經過整理的數列中你想要找到一個特定數字，就必須從頭開始找。最糟糕的情況就是找到數列結尾發現這個數字根本不再數列中。時間複雜度會來到`O(n)`。如果你**一開始有把數字排列好，你就能用其他更快方法來找數字了**。接下來我會向你展現演算法的奧妙!膜拜吧!(還真是高高在上呢!)

**比較演算法**分為兩大類，比較排序 & 非比較排序，往下讀你就知道甚麼叫做 **比較** 以及 **非比較** 了

:::spoiler **average time**(點我展開)
> 在這邊說一下，下文中會出現一個新的概念，**average time**。 average time 指的是演算法運行平均所需要花的時間，在下文中用 `θ(f(n))`代表。(但看過上一篇文章中先備知識[《數學上的時間複雜度》](https://mycollegenotebook.medium.com/%E6%99%82%E9%96%93%E8%A4%87%E9%9B%9C%E5%BA%A6-%E6%BC%B8%E9%80%B2%E5%87%BD%E6%95%B8-397ca19cdc4c)的你應該知道`θ(f(n))`的意義並不是這樣吧!你應該有去看過這篇文章齁!沒看趕快去看!)
:::

## <font size=6>比較排序</font>
甚麼是比較排序呢？比較排序顧名思義，就是**透過元素的兩兩比較來進行排序**。
假設今天有`a`,`b`兩個元素，排序他們的方法就是利用 `a<b` 這個判斷式來進行排序。
如果判斷式是 `True`。排序結果就是 `a,b`，反之，則 `b,a`。
<!-- 有時間的話補充個逆對概念-->

我這邊先來教你比較淺顯易懂的排序的演算法。

### 範例1:排序長度為 `n` 的數列
> ```
> n
> a1 a2 a3 a4 ... an
> ```
> 第一行輸入`n` 為數列長度
> 第二行數入為所有數列元素，以空白鍵相隔。

### Bubble Sort (範例1)
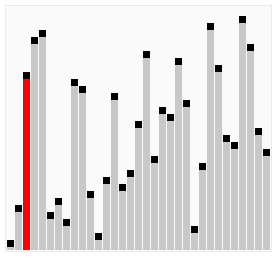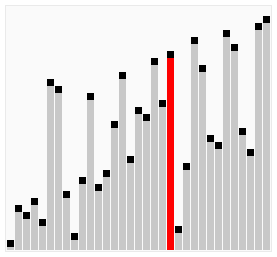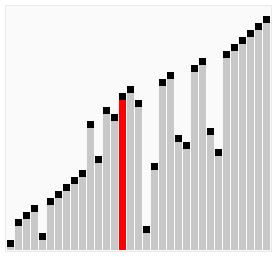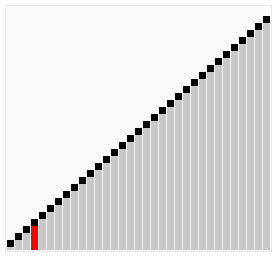
> Bubble Sort 就是透過不斷地交換讓較大的數字逐漸「浮」到正確位置，下面我來用動畫進行演式吧。
> ### 動畫
> 
> ### 程式碼
> ```python=
> def bubble_sort(arr):
>
> # 外迴圈執行 n-1 次
> for n in range(len(arr) - 1, 0, -1):
> swapped = False　　　#用來檢查內迴圈到底有沒有執行swap
>
> # 內迴圈進行元素的比較，並讓比較大的數字「浮」到後面
> for i in range(n):
> 　　 #如果第 i 的數字大於 第i+1的，就進行一次交換
> if arr[i] > arr[i + 1]:
> arr[i], arr[i + 1] = arr[i + 1], arr[i]
> swapped = True　　　#標記swap有被執行
>
> # 如果內迴圈都沒有執行 swap 就代表數列已經整理好了
> if not swapped:
> break
> ```
> **程式碼動畫**
> 
> ### 時間複雜度
> **最壞情況 `O(n^2)`**
> 完全倒過來->也就是程式全部跑完，沒有被`swapped`結束
> **平均情況 `θ(n^2)`**
> 你可以用最小元素位置在哪?為出發點來計算為什麼時間複雜度是這樣

### Insertion Sort(範例1)
> 你應該玩過大老二吧!在整理手中的撲克牌時，每次從右邊未排序的部分取出一張撲克牌，插到左邊已排序的部分。這就是Insertion Sort，讓我再用動畫讓你好理解一點。
> ### 動畫
> 
>
> ### 程式碼
> ```python=
> def insertionSort(arr):
> n = len(arr) # 數列的長度
>
> if n <= 1:
> return # 如果數列長度為 0 或是 1 就代表根本不需要排序
>
> for i in range(1, n): #跑 n-1 次迴圈，i代表 arr 在 i 之前都已經排序好了
> key = arr[i] # arr[i] 現在要插入 arr[0] ~ arr[i-1]之中
> j = i-1
> while j >= 0 and key < arr[j]: # 當key < arr[j]時，把arr[j]往後挪一格
> arr[j+1] = arr[j] # Shift elements to the right
> j -= 1
> arr[j+1] = key # 將 key 插到空出來的位置中
> ```
> **程式碼動畫**
> 
> ### 時間複雜度
>**最壞情況 `O(n^2)`**
> 數列是倒敘時，每次 `j` 都會跑到 `0`，因此時間複雜度是 `n(n-1)/2 = O(n^2)`
> **平均情況 `θ(n^2)`**
> 程式外迴圈執行到 `i` 時, `j`平均下來會跑 `i/2`，，因此時間複雜度是 `O(n^2)`
> :::spoiler **平均情況 `θ(n^2)`更詳細解釋**(點我展開)
> 對於大小為 `n` 的數列
> - 第一個元素已經過簡單排序，因此不需要任何操作。
> - 將第二個元素與前一個元素進行比較，並插入正確的位置
> → 執行1次（平均）。
> - 將第三個元素與前兩個元素進行比較，並插入正確的位置
> → 執行1 或 2 次（平均）。
> - 第四個個元素與前三個元素進行比較，並插入正確的位置
> → 執行1 ~ 3 次（平均）。
> ...
> $$
> \begin{aligned}
> \sum_{i=1}^{n-1} \frac{i}{2} &= \frac{1}{2} \sum_{i=1}^{n-1} i = \frac{1}{2} \cdot \frac{(n-1)n}{2} = \frac{n^2 - n}{4} = O(n^2)
> \end{aligned}
> $$
> :::

除了以上兩種時間複雜度為 `O(n^2)` 的排序法外，其實還有其他更快的演算法，可以把時間複雜度壓到 `O(n*log(n))`。例如:**quick sort, merge sort, heap sort**。但是 **quick sort** 和 **merge sort** 會牽涉到**分治**的概念，而 **heap sort**會牽涉到**圖論**，所以到分治法、圖論的章節才會再進行介紹。

另外，比較排序法的時間複雜度最低只能壓到`O(n*log(n))`，至於為什麼你可以看看這篇文章 [《基于比较排序的时间复杂度的下界》](https://blog.csdn.net/qq_38206090/article/details/82381648)

## <font size=6>非比較排序</font>
那非比較排序又是甚麼呢？比較排序顧名思義，就是**不**透過元素的兩兩比較來進行排序。
比較排序不依賴元素間的比較來確定順序，而是利用數據的某些特性來進行排序，所以非比較排序的時間複雜度有可能比`O(n*log(n))`小。

接下來，我們將介紹兩種常見的非比較排序演算法。
### 範例2:
> 排序以下數列
> `170 45 75 90 802 24 2 66`

### counting sort(範例2)
> 統計每個元素出現的次數，然後根據這些次數直接計算出每個元素在排序後數列中的最終位置。
> ### 動畫
> [《counting sort 動畫》](https://media.geeksforgeeks.org/wp-content/uploads/20240723235224/ezgifcom-gif-maker2.mp4?_=2)
> ### 程式碼
> ```python=
> def counting_sort(arr):
> if not arr:
> return []
>
> # 1. 找出數字範圍(假設所有值都>=0)
> max_val = arr[0]
> for x in arr:
> if x > max_val:
> max_val = x
>
> # 2. 建立計數陣列
> k = max_val + 1 # 數字範圍為 0 ~ max_val
> count = [0] * k
>
> # 3. 統計次數，每個數字分別出現幾次
> for x in arr:
> count[x] += 1
>
> # 4. 計算累計次數
> for i in range(1, k):
> count[i] += count[i-1]
>
> # 5. 建立輸出陣列
> output = [0] * len(arr)
>
> # 6. 放置元素 (從後向前以確保相同值的數字不會被反過來放)
> i = len(arr) - 1
> while i >= 0:
> element = arr[i]
> # count[element]-1 是元素在 output 中的正確索引
> output[count[element] - 1] = element
> count[element] -= 1 # 將計數減 1
> i -= 1
>
> return output
>
> ```
> ### 時間複雜度
> 時間複雜度為 `O(n+k)`，k為所有數字的範圍大小`[0,max_val]`
> `O(n)`：遍歷輸入數列以找到最大值（步驟 1）。
> `O(k)`：初始化計數陣列（步驟 2）。
> `O(n)`：遍歷輸入數列以統計次數（步驟 3）。
> `O(k)`：遍歷計數陣列以計算累計次數（步驟 4）。
> `O(n)`：遍歷輸入數列以放置元素到輸出陣列（步驟 6）。

### radix sort (範例2)
> Radix Sort 也是一種 非比較排序 演算法，它不直接比較元素的大小，而是根據元素的各個**位數**進行排序。從**最低位**開始，逐位進行排序，直到**最高位**。
> ### 動畫
> 
> ### 程式碼
> ```python=
> # Radix Sort 內部使用的 Counting Sort (針對特定位數)
> def counting_sort_for_radix(arr, exp):
> n = len(arr)
> output = [0] * n
> count = [0] * 10 # 十進制，所以只需要 0-9 的計數
>
> # 計算每個數字在 exp 位上的出現次數
> for i in range(n):
> index = (arr[i] // exp) % 10 # 取得對應位數的數字
> count[index] += 1
>
> # 計算累計次數
> for i in range(1, 10):
> count[i] += count[i - 1]
>
> # 建立輸出陣列 (從後向前保持穩定性)
> i = n - 1
> while i >= 0:
> index = (arr[i] // exp) % 10
> output[count[index] - 1] = arr[i]
> count[index] -= 1
> i -= 1
>
> # 將排序好的結果複製回 arr
> for i in range(n):
> arr[i] = output[i]
>
> def radix_sort(arr):
> if not arr:
> return []
>
> # 1. 找到最大值以確定最大位數
> max_val = arr[0]
> for x in arr:
> if x > max_val:
> max_val = x
>
> # 2. 從最低位 (exp=1) 開始，對每一位進行 Counting Sort
> exp = 1 # 代表目前處理的位數 (1, 10, 100, ...)
> while max_val // exp > 0:
> counting_sort_for_radix(arr, exp)
> exp *= 10 # 移到下一位 (十位、百位...)
>
> return arr # arr 本身已經被修改
> ```
> ### 時間複雜度
> 令 `n` 為輸入數列的元素個數。
> 令 `b` 為基數 (base)，對於十進制整數，`b=10`。
> 令 `d` 為最大元素是幾位數字 (`max_element = k*b^d`,`k`為常數)。
> Radix Sort 的每一輪都需要對 n 個元素根據某一位數進行穩定排序。如果使用 Counting Sort 作為內部排序，每一輪的時間複雜度是 `O(n+b)`。總共需要進行 `d` 輪排序。
>因此，Radix Sort 的總時間複雜度為 `O(d⋅(n+b))`。
>:::spoiler **穩定的內部排序法**(點我展開)
>Radix Sort 需要一個穩定(static)的內部排序演算法來對每個位數進行排序。
>假設一組序列第`t-1`位已經完成排序，我們想要對第`t`位進行排序。對第`t`位來排序有兩種狀況
> * 如果兩個元素的第`t`位是相同的，也就是有兩個元素在第`t`位有相同的數字，則他們排序的順序會由第`t-1`位來決定。如我此時我的內部演算法是不穩定的，那在第`t`位之前的排序就會失效，也就是我無法以第`t-1`位來做排序依據。
> * 如果這兩個元素第`t`位是不相同的，就不用再往下看其他位數。
>
>從這個證明可以發現到，排序本身必須要具有穩定性。
>> #### 穩定排序法(stable sorting)
>> 如果鍵值相同之資料，在排序後相對位置與排序前相同時，稱穩定排序。
>> * 排序前`3,5,19,1,3*,10`
>> * 排序後`1,3,3*,5,10,19` (因為兩個3, 3*的相對位置在排序前與後皆相同。)
>> #### 不穩定排序法(unstable sorting)
>> 如果鍵值相同之資料，在排序後相對位置與排序前不相同時，稱不穩定排序。
>> * 排序前`3,5,19,1,3*,10`
>> * 排序後`1,3*,3,5,10,19` (因為兩個3, 3*的相對位置在排序前與後不相同。)
>:::

---
> 上一篇文章　[時間複雜度](https://hackmd.io/@iDoNotWantToCoding/SJosmXioJl)
> 下一篇文章　[前綴合](https://hackmd.io/@iDoNotWantToCoding/S1vxNmsoJe)
> 先備知識　　無
> 延伸閱讀　　[基于比较排序的时间复杂度的下界](https://blog.csdn.net/qq_38206090/article/details/82381648)