<style> .reveal, .reveal h1, .reveal h2, .reveal h3, .reveal h4, .reveal h5, .reveal h6 { font-family: "Source Sans Pro", "Helvetica Neue", Helvetica, Arial, "Microsoft JhengHei", Meiryo, sans-serif; } h1, h2, h3, h4, h5, h6 { text-transform: none !important; } .color-yellow{ color: yellow; } .alert { padding: 15px; margin-bottom: 20px; border: 1px solid transparent; border-radius: 4px; text-align: left; padding: 10px 0; } .alert-info { color: #31708f; background-color: #d9edf7; border-color: #bce8f1; } .alert-success { color: #3c763d; background-color: #dff0d8; border-color: #d6e9c6; } .alert-danger { color: #a94442; background-color: #f2dede; border-color: #ebccd1; } .reveal .slides span { text-align: left; display: inline-block; } p, li { font-size: 0.88em !important; } li>p { font-size: 1em !important; } </style> # JuliaTokai #10 (2021/05/15) ###### tags: `JuliaTokai` `prezentation` --- # Rotations.jlで学ぶ<br>3次元の回転 [堀川 由人, ほりたみゅ, @Hyrodium](https://hyrodium.github.io) ---- ### おしながき * 自己紹介 * 3次元の回転って？ * Rotations.jlの紹介 * 面白い結果(a) $\operatorname{SO}(3)$の可視化 * 面白い結果(b) Thomson問題の拡張 * まとめ --- ## 自己紹介 幾何学がスキ！   [堀川 由人, ほりたみゅ, @Hyrodium](https://hyrodium.github.io) * 過去の関連発表 * Rotations.jlとの関わり ---- ### 過去の関連発表 $\operatorname{SO}(3)$と$\operatorname{SU}(2)$の対応関係について話しました * [逆数の作図からCayley変換まで / 第1回日曜数学会](https://www.slideshare.net/yutohorikawa/cayley-57826500)    * [Riemann球面に内接する直方体 / 第4回日曜数学会](https://www.slideshare.net/yutohorikawa/riemann-57827572)    ---- ### Rotations.jlとの関わり 3次元回転をJuliaで扱うためのパッケージ * 1ヶ月前(2021/04/08)からcontribution開始 * PR 8つ (merged 3つ) * issue 7つ * 3次元回転を完全に理解したぞ！ * 今日はその報告です --- ## 3次元の回転って？ * そもそも回転とは * $\operatorname{SO}(3)$の性質 ①-⑥ ---- ### そもそも回転とは * 原点の位置を変えない合同変換 * (普通は)Eudlid空間での合同変換 * ただし鏡像は除く * 線形代数の言葉で言えば… * 直交行列による変換 ($R^{-1}=R^{\top}$となる行列) * ただし行列式は1 * 一般には$n$次の回転行列まで考えれる * $\operatorname{SO}(n)$と書く * Rotations.jlでは(基本的に)3次のみ扱う ---- ### $\operatorname{SO}(3)$の性質① 元の可視化 $\color{red}{x},\color{green}{y},\color{blue}{z}$軸の正規直交基底の"姿勢"が$\operatorname{SO}(3)$の元   ---- ### $\operatorname{SO}(3)$の性質② 空間の次元 * 与えられた姿勢への到達に、3回の座標軸回転が必要 * Euler角と呼ばれる (回転順序によって12種類存在) * $\color{blue}{z}\text{-}\color{red}{x}\text{-}\color{blue}{z}, \color{red}{x}\text{-}\color{green}{y}\text{-}\color{red}{x}, \color{green}{y}\text{-}\color{blue}{z}\text{-}\color{green}{y}, \color{blue}{z}\text{-}\color{green}{y}\text{-}\color{blue}{z}, \color{red}{x}\text{-}\color{blue}{z}\text{-}\color{red}{x}, \color{green}{y}\text{-}\color{red}{x}\text{-}\color{green}{y}$ 狭義Euler角 * $\color{red}{x}\text{-}\color{green}{y}\text{-}\color{blue}{z}, \color{green}{y}\text{-}\color{blue}{z}\text{-}\color{red}{x}, \color{blue}{z}\text{-}\color{red}{x}\text{-}\color{green}{y}, \color{red}{x}\text{-}\color{blue}{z}\text{-}\color{green}{y}, \color{blue}{z}\text{-}\color{green}{y}\text{-}\color{red}{x}, \color{green}{y}\text{-}\color{red}{x}\text{-}\color{blue}{z}$ Tait–Bryan角 * つまり$\operatorname{SO}(3)$は3次元の空間！ $\dim(\operatorname{SO}(3))=3$ * より一般に$\dim(\operatorname{SO}(n))=n(n-1)/2$ 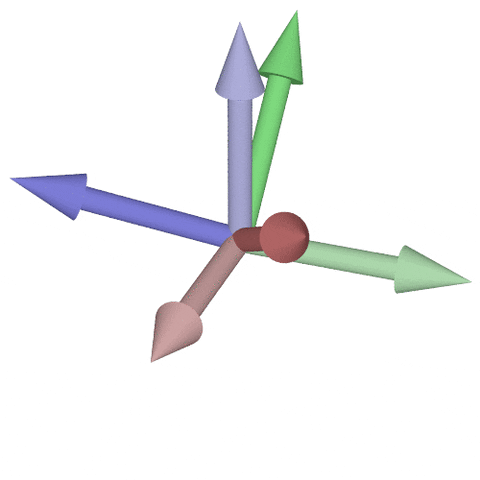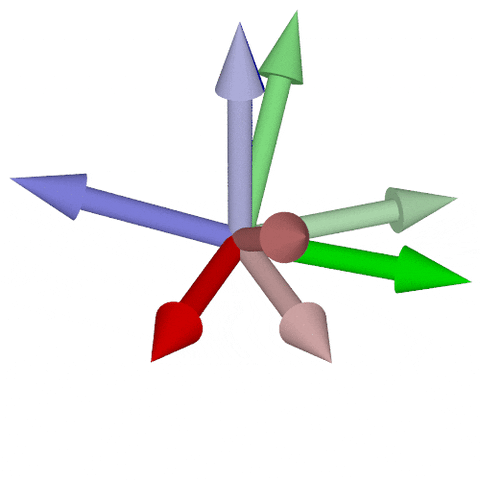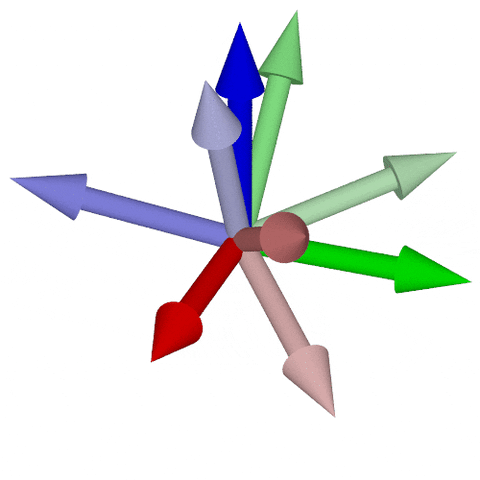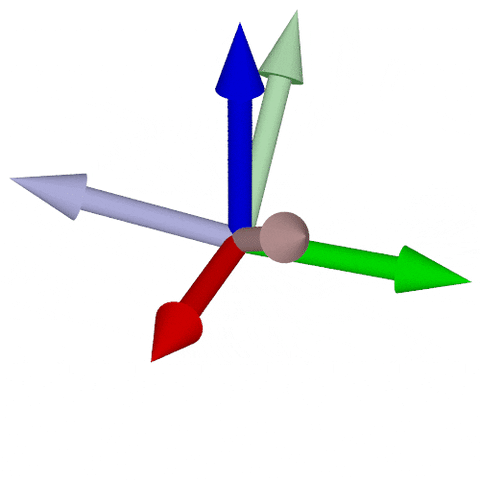 \ $\color{red}{x}\text{-}\color{green}{y}\text{-}\color{blue}{z}回転　/　\color{red}{x}\text{-}\color{green}{y}\text{-}\color{red}{x}$回転 ---- ### $\operatorname{SO}(3)$の性質③ 行列表示   * 3次元なのにパラメータが9つあるように見える * $xy$平面上の円周$S^1$と同じ状況 * 行列表示すると過剰にパラメータが発生 * :arrow_up: 計算量 * :arrow_down: 計算精度 * 行列表示以外の"良い"パラメータが欲しい！ ---- ### $\operatorname{SO}(3)$の性質④ 固有値と固有ベクトル * $R\in \operatorname{SO}(3)$の固有値は$\{1,e^{i\theta},e^{-i\theta}\}$で表示可能 * 固有値$1$に対応する固有ベクトルが回転軸 * $\theta$が回転角 * 任意の回転は「軸回りの回転」として表示可能！ * 回転軸(2次元)+回転量(1次元)なのでちゃんと3次元 * [Rodriguesの回転公式](https://ja.wikipedia.org/wiki/%E3%83%AD%E3%83%89%E3%83%AA%E3%82%B2%E3%82%B9%E3%81%AE%E5%9B%9E%E8%BB%A2%E5%85%AC%E5%BC%8F)   ---- ### $\operatorname{SO}(3)$の性質⑤ 準同型な空間など この辺りから数学的に込み入ってきますが… * $\operatorname{SO}(3)$と$\operatorname{SU}(2)$は$1:2$に対応(準同型) * $\operatorname{SU}(2)$は$\det$が1のユニタリ行列全体 * (詳細は以前の発表スライド参照) * $\operatorname{SU}(2)$は「単位長さ四元数全体」と対応(同型) * つまり4つの実数で3次元の回転を表現可能 * パラメータ減ってハッピー！(9→4) * 「単位長さ四元数」は3次元球面$S^3$と対応(同相) * $S^3\subset\mathbb{R}^4$なので普通の球面ではない * 立体射影で$S^3\leftrightarrow\mathbb{R}^3\cup\{\infty\}$の対応(同相) * パラメータ減ってハッピー！(4→3) ---- ### $\operatorname{SO}(3)$の性質⑥ まとめ * $\operatorname{SO}(3)$は3次元Lie群！ * 3次行列として表示可能 * しかし計算には都合が悪い * 良い感じのパラメータ(座標)が欲しい！ * 直感的に理解しやすい * コンピュータが計算しやすい * 数学的なモチベーション → https://twitter.com/phykm/status/1388747029304672261 * 行列表示 / Euler角 / 軸回り回転 / 四元数 / $\mathbb{R}^3\cup\{\infty\}$ --- ## Rotations.jlの紹介 * Juliaで3次元回転を扱うためのパッケージ比較 * Rotations.jlで定義される型 * 使い方の例 ---- ### Juliaで3次元回転を扱うための<br>パッケージ比較 * [Rotations.jl](https://github.com/JuliaGeometry/Rotations.jl) * 回転は3次元行列 * 最新版`v1.0.2` * [ReferenceFrameRotations.jl](https://github.com/JuliaSpace/ReferenceFrameRotations.jl) * (まだ詳しく触ってないので何とも…) * 最新版`v0.5.7` ---- <!-- .slide: style="font-size: 30px;" --> ### Rotations.jlで定義されている型 * 行列表示 * `RotMatrix` * Euler角 * `RotX`, `RotY`, `RotZ` * `RotXY`, `RotYX`, `RotZY`, `RotYZ`, `RotXZ`, `RotZX` * `RotXYZ`, `RotXYX`, (他10種) * 軸回り回転 * `AngleAxis` * `RotationVec` * 四元数 * `UnitQuaternion` * $S^3$の立体射影 * `MRP` (Modified Rodrigues Parameters) * $S^3$の原点からの射影 * `RodriguesParam` `<: Rotation <: StaticMatrix <: AbstractMatrix` これらの他にも2次元回転の型もある ---- ### 使い方の例 ```julia= using Rotations # ランダムに回転行列を生成 (Haar測度) R_uq = rand(UnitQuaternion{Float64}) # 行列に変換 Matrix(R_uq) # 別のパラメータに変換 (MRP) R_mrp = MRP(R_uq) # 別のパラメータに変換 (Euler角) R_xyz = RotXYZ(R_uq) ``` このスライドのgifもRotations.jlで計算してます (レンダリングはPOV-Ray) --- ## 面白い結果(a) $\operatorname{SO}(3)$の可視化 `MRP`を使えば頑張れば$\operatorname{SO}(3)$を3次元球として描ける！ * ① 可視化の概要 * ② 座標軸まわりの回転 * ③ 非可換性の可視化 * ④ $xy$回転曲面の可視化 * ⑤ ジンバルロック * ⑥ 有限部分群 ---- ### $\operatorname{SO}(3)$の可視化① `MRP`で可視化する！   数学的に込み入ったことは抜きにして… 3次元球内の一点が、一つの姿勢($\operatorname{SO}(3)$の元)を表す！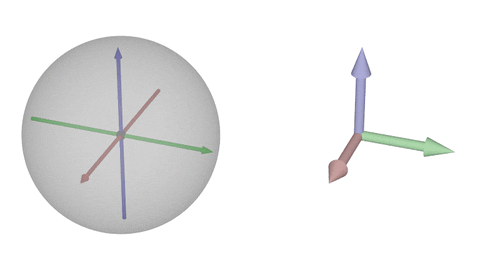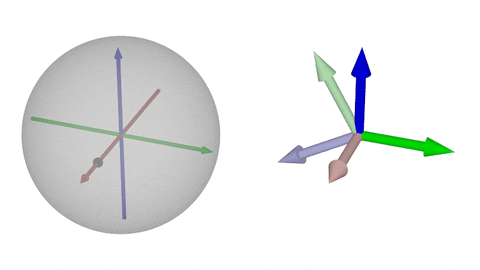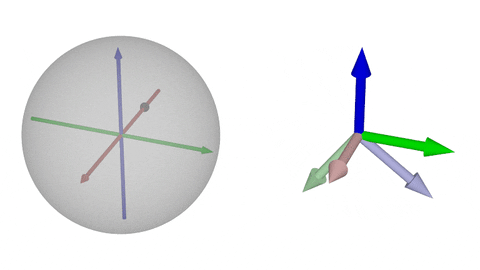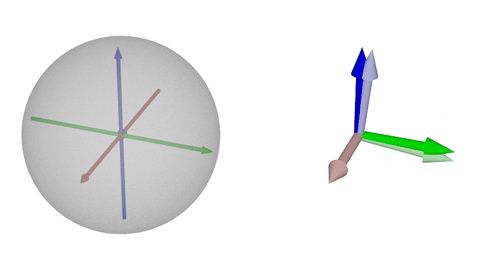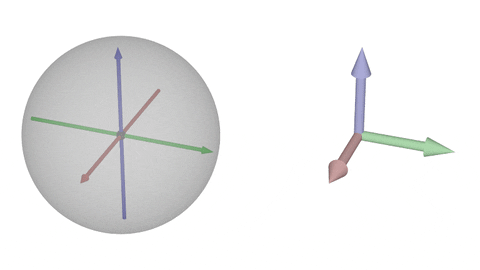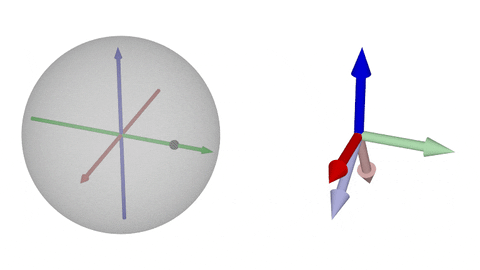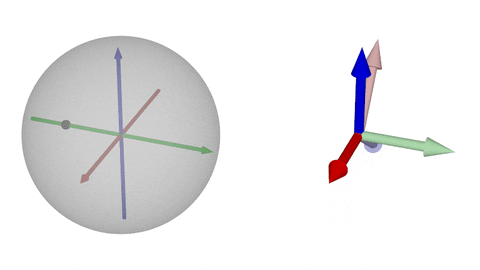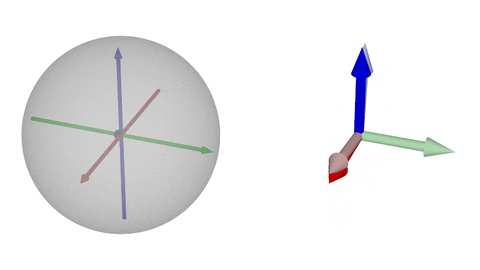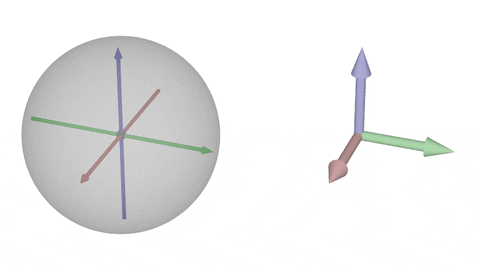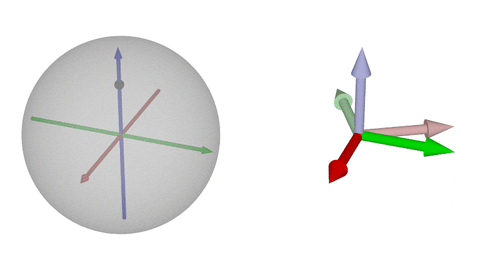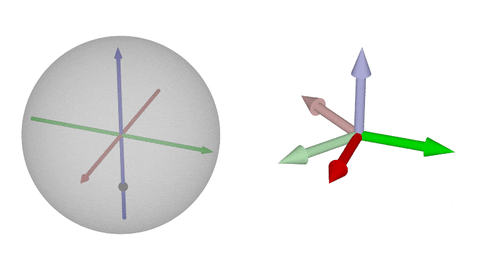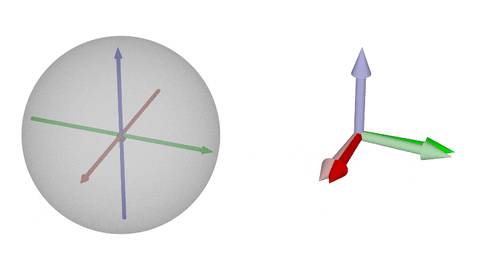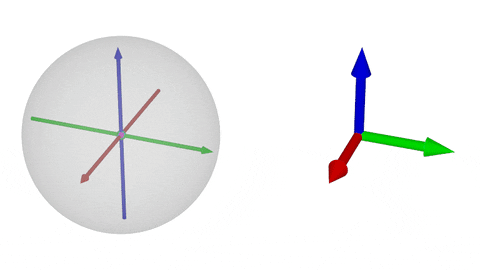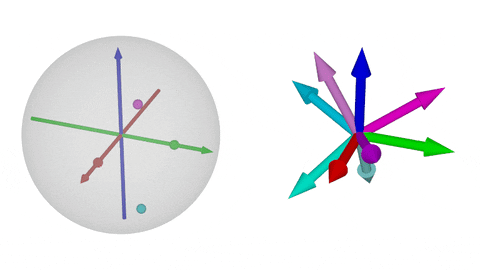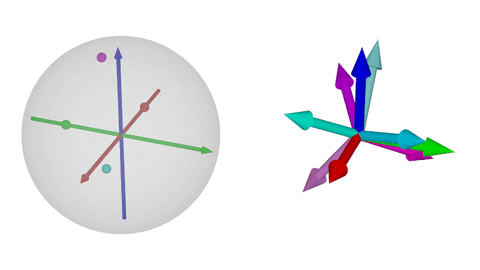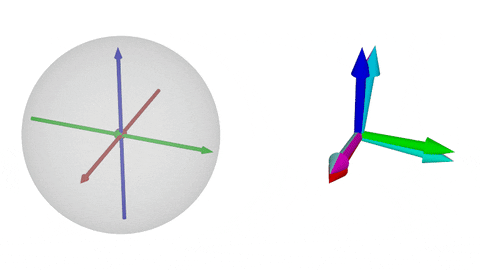 ---- ### $\operatorname{SO}(3)$の可視化②-x $x$軸回転  原点が単位行列 ---- ### $\operatorname{SO}(3)$の可視化②-y $y$軸回転  球面上の点がちょうど「180°回転」に相当する ---- ### $\operatorname{SO}(3)$の可視化②-z $z$軸回転  * 一般に左図での「球面内の点と原点を結ぶ直線」は右図での「回転軸」に一致する * 逆元は原点対称の点 ---- ### $\operatorname{SO}(3)$の可視化③ $\operatorname{SO}(3)$の非可換性：$\color{magenta}{R_x(t)R_y(t)}$と$\color{cyan}{R_y(t)R_x(t)}$の比較  MRP(左)の方が基底の図示(右)よりも把握しやすい ---- ### $\operatorname{SO}(3)$の可視化④ $\{R_x(s)R_y(t) \mid s,t\in\mathbb{R}\}$は群を成さないが… 曲面としては描画できる   ---- ### $\operatorname{SO}(3)$の可視化⑤ [ジンバルロック](https://ja.wikipedia.org/wiki/%E3%82%B8%E3%83%B3%E3%83%90%E3%83%AB)(`RotXYX`)  $x$軸上でめっちゃ密 😷 → Jacobianがゼロ → Euler角は$\operatorname{SO}(3)$の全体座標に不適格 ---- ### $\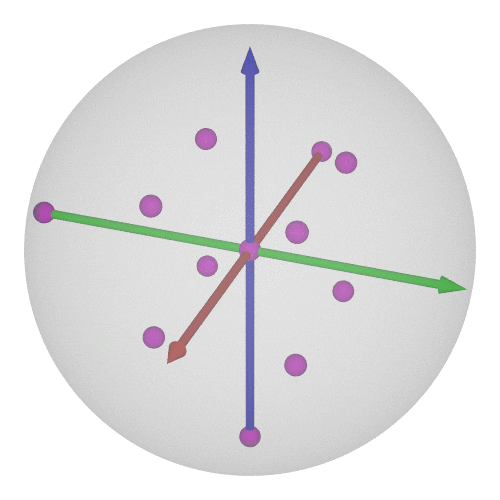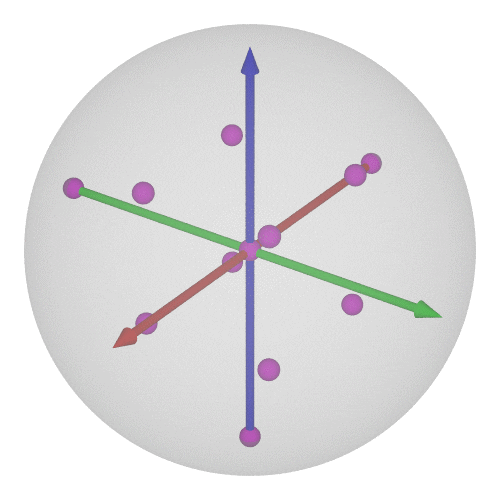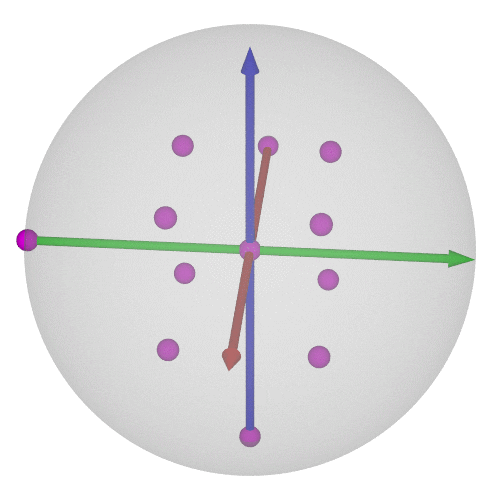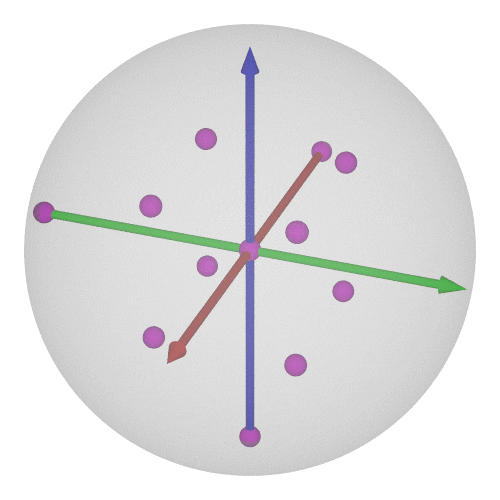operatorname{SO}(3)$の可視化⑥-4/4 $\operatorname{SO}(3)$の有限部分群と言えば…正多面体群！ * 正4面体群の位数は12 * $\operatorname{SU}(2)$で考えれば24個←正24胞体の頂点に一致！   ---- ### $\operatorname{SO}(3)$の可視化⑥-6/8 * 正6面体群(=正8面体群)の位数は24 * $\operatorname{SU}(2)$で考えれば48個←正24胞体の頂点と胞中心に一致！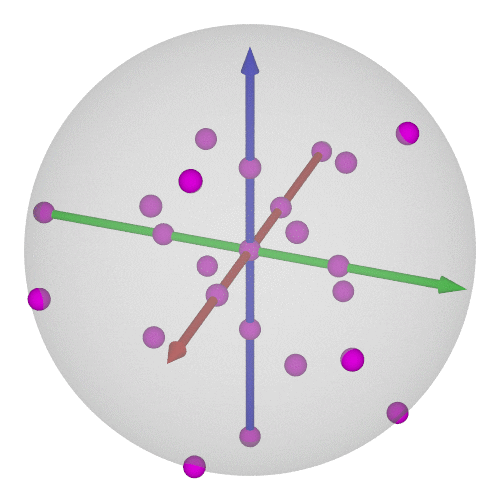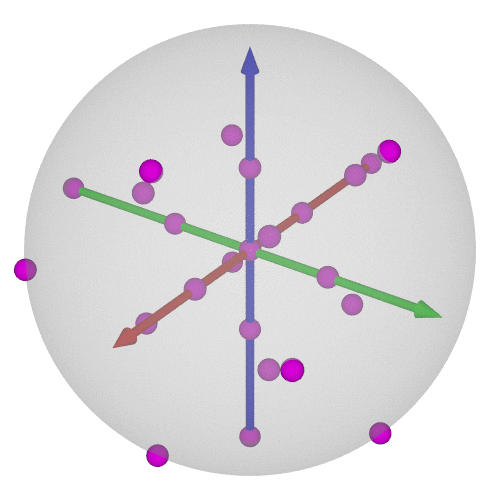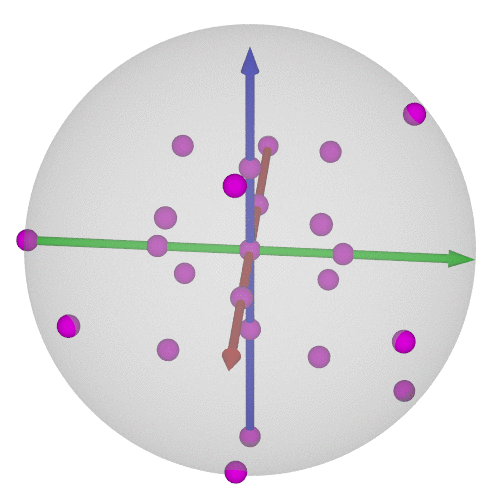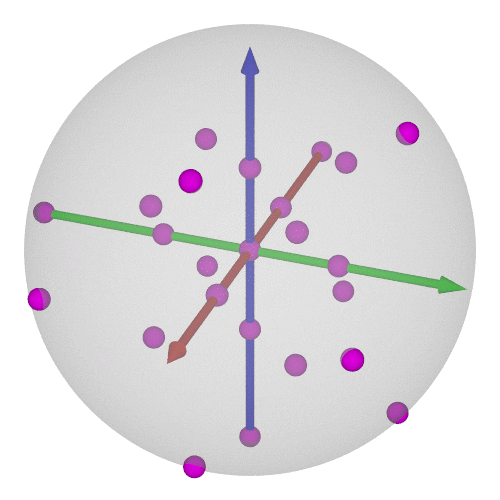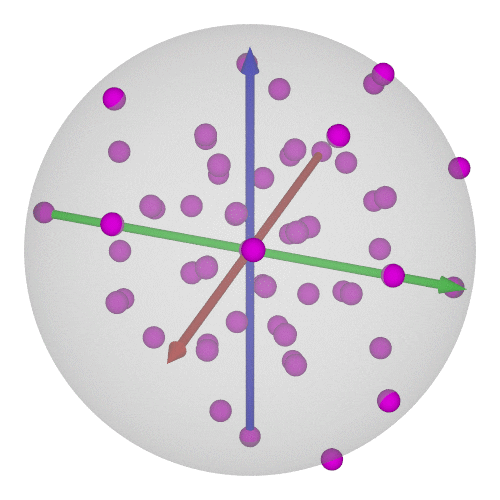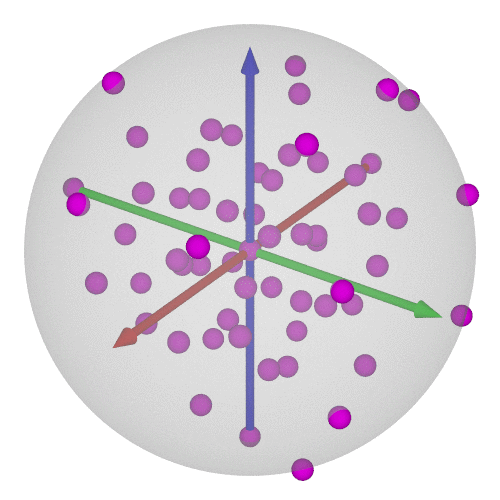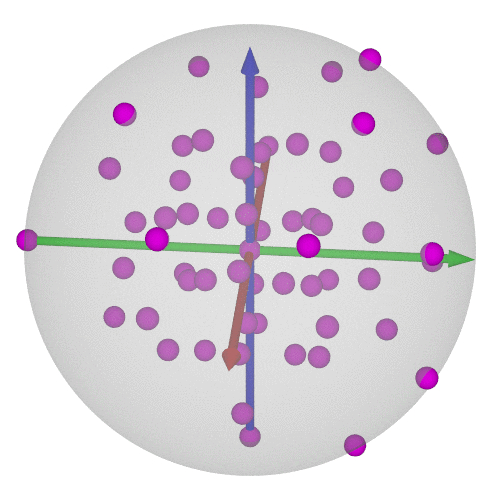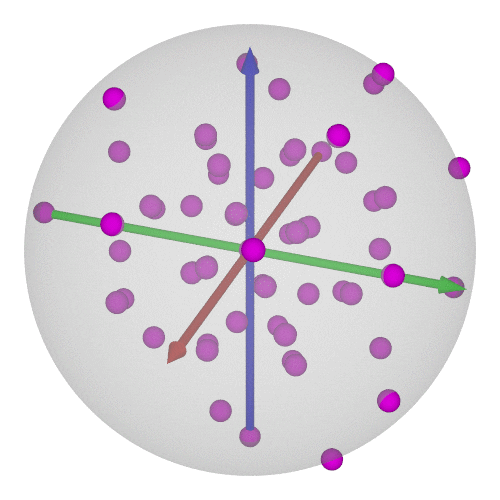   ---- ### $\operatorname{SO}(3)$の可視化⑥-12/20 * 正12面体群(=正20面体群)の位数は60 * $\operatorname{SU}(2)$で考えれば120個←正600胞体の頂点に一致！   --- ## 面白い結果(b) Thomson問題の拡張 * Thomson問題とは * $\operatorname{SO}(3)$への拡張 * 計算結果 ---- ### Thomson問題とは① 概要 > トムソン問題（トムソンもんだい、英: Thomson problem） は、静電エネルギーが最小になるよう単位球面上に N 個の電子を配置する問題である（電子間力はクーロンの法則に従うものとする）。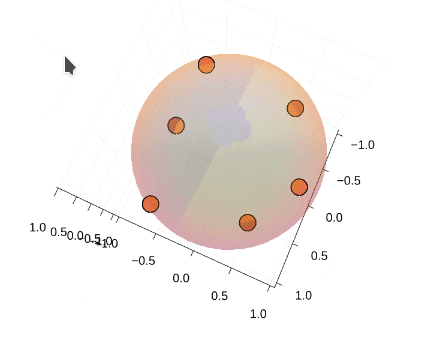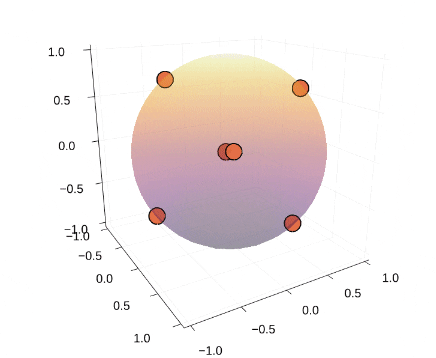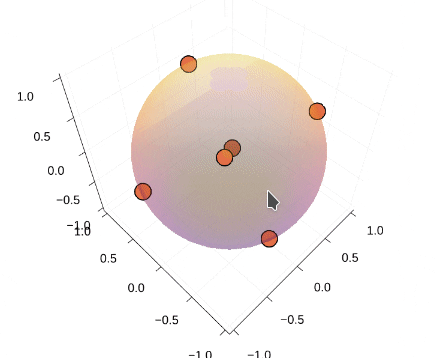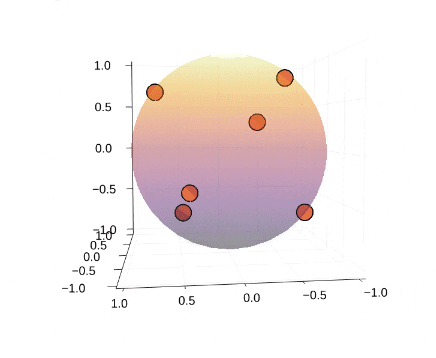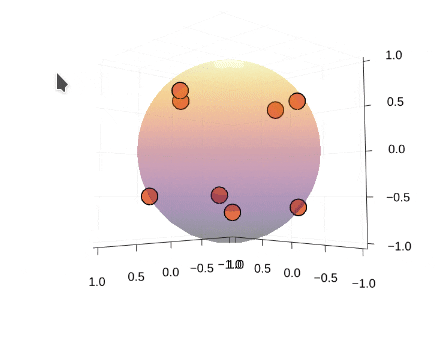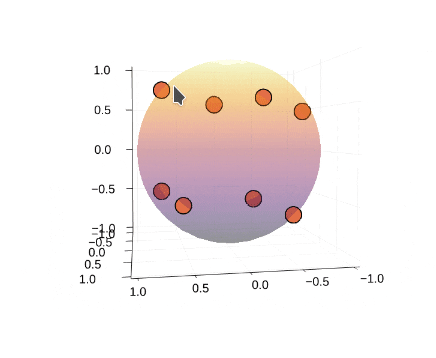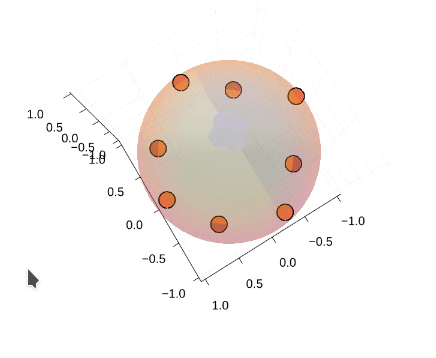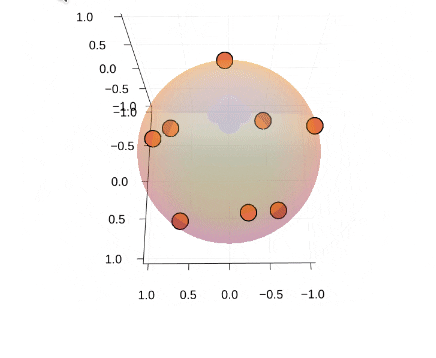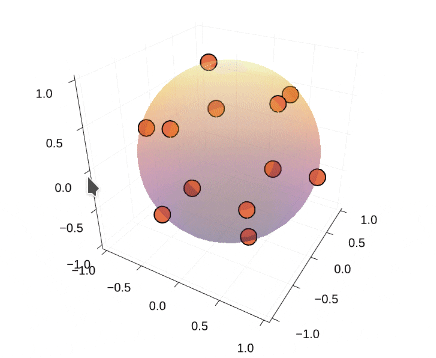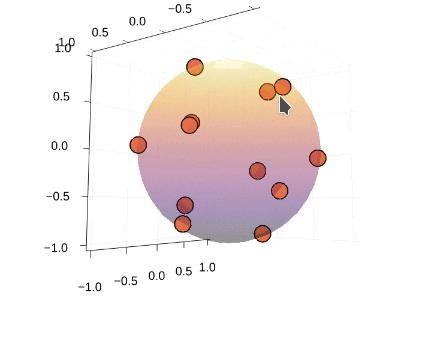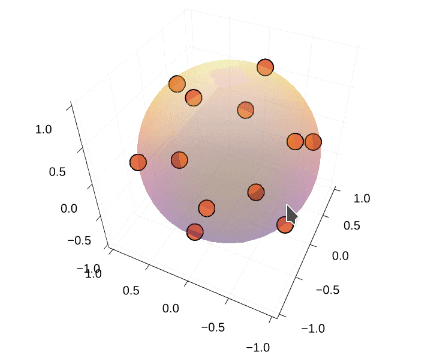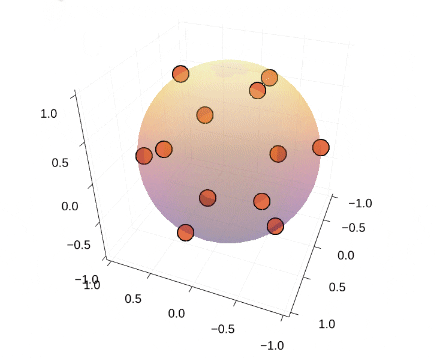 [Wikipedia](https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%A0%E3%82%BD%E3%83%B3%E5%95%8F%E9%A1%8C)より ---- ### Thomson問題とは② 計算例      * 4,6,8,12,20点で計算 * 4,6,12点の場合のみ、正多面体の頂点に一致 ---- ### $\operatorname{SO}(3)$への拡張 * そもそも$\operatorname{SO}(3)$にどうやって距離いれるの？ * 2点間を結ぶ回転行列の回転角にしよう！ * Lie代数$\mathfrak{so}(3)$に内積($\operatorname{SO}(3)$にRiemann計量)を入れて「最短曲線の長さ」を距離とすることと同じ * じゃあエネルギーは？ * Thomson問題に倣って(1/距離)を2点間のエネルギーにしよう！ ---- ### 計算結果 * 12,24,60点で正多面体群が出てくると期待されるが… * 正多面体群になるのは24,60点のみだった！ <small/>(数値的に実験しただけで厳密に示した訳ではないです)</small> * スライドが間に合わなかったのでデモします… --- ## まとめ * 感想 * 今後の予定 * 参考文献など ---- ### 感想 * Rotations.jl便利！ * いろんなパラメータ変換とか有り難い * 可視化にも便利 * コンストラクタのベストプラクティスが分からん… * コンストラクタで正規化するか否か ---- ### 今後の予定 * Rotations.jlのバグ修正 * 私が送ったPR早くレビューして欲しいな:pray::pray::pray: * もう少し真面目にThomson問題を解く * 微分方程式系として記述できそう * ちゃんと可視化もやる ---- ### 参考文献など * [Rotations.jl](https://github.com/JuliaGeometry/Rotations.jl) * Rotations.jlのリポジトリ * [逆数の作図からCayley変換まで / 第1回日曜数学会](https://www.slideshare.net/yutohorikawa/cayley-57826500) * 私の以前の発表 * [Riemann球面に内接する直方体 / 第4回日曜数学会](https://www.slideshare.net/yutohorikawa/riemann-57827572) * 私の以前の発表 * [EquallySpacedPointsOnSO3](https://github.com/hyrodium/EquallySpacedPointsOnSO3) * $\operatorname{SO}(3)$上でのThomson問題のリポジトリ * [VisualizeSO3](https://github.com/hyrodium/VisualizeSO3) * このスライドでの図を作ったときのリポジトリ * 他にも個人ブログ等で参考にしたのあったはず…:pray: