# Transformer Lesson - Part 1/7: Introduction and Architecture

## 1. Introduction to Transformers

Transformers, introduced in the seminal paper ["Attention Is All You Need"](https://arxiv.org/abs/1706.03762) by Vaswani et al. (2017), revolutionized natural language processing by replacing recurrent and convolutional layers with self-attention mechanisms.

Key advantages:
- Parallel processing of sequences (unlike RNNs)
- Ability to capture long-range dependencies
- Scalability to large models

## 2. Basic Transformer Architecture

The original transformer architecture consists of:


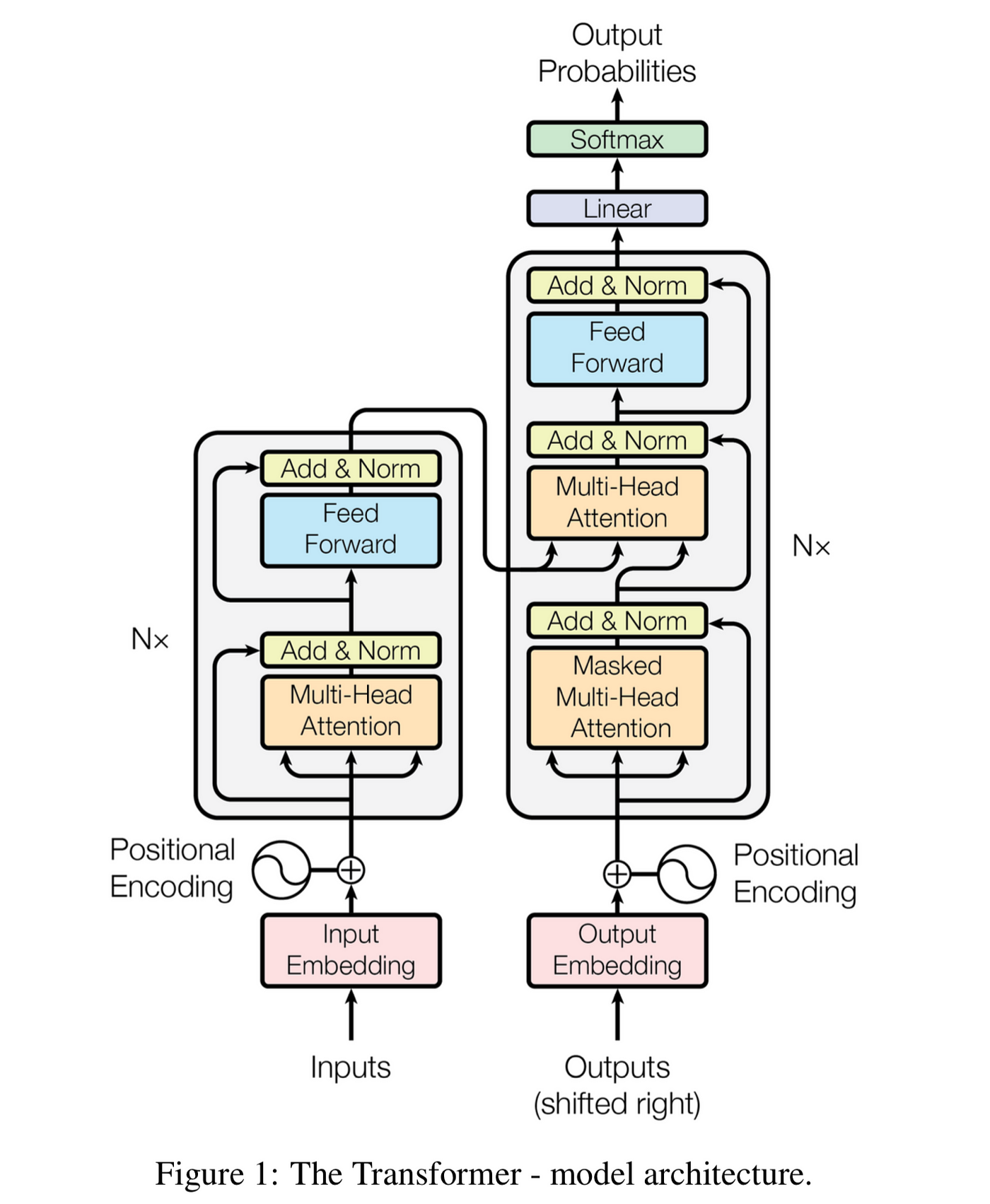
*Original transformer architecture diagram from the "Attention Is All You Need" paper*

Mathematically, the transformer can be represented as:

$$\text{Transformer}(X) = \text{Decoder}(\text{Encoder}(X))$$

Where:
- $X$ is the input sequence
- Encoder processes the input
- Decoder generates the output

## 3. Core Components

### 3.1 Encoder

The encoder consists of multiple identical layers (typically 6 in the original paper), each with:

1. Multi-head self-attention mechanism
2. Position-wise feed-forward network
3. Residual connections and layer normalization

The encoder process can be represented as:

$$\text{EncoderLayer}(X) = \text{LayerNorm}(X + \text{FFN}(\text{LayerNorm}(X + \text{MultiHeadAttention}(X))))$$

### 3.2 Decoder

The decoder also consists of multiple identical layers with three main sub-layers:

1. Masked multi-head self-attention
2. Multi-head encoder-decoder attention
3. Position-wise feed-forward network

The decoder process is:

$$\text{DecoderLayer}(X, \text{EncOutput}) = \text{LayerNorm}(X + \text{FFN}(\text{LayerNorm}(X + \text{MultiHeadAttention}(X, \text{EncOutput}))))$$

## 4. Self-Attention Mechanism

The key innovation in transformers is the self-attention mechanism, which computes attention weights between all positions in the sequence.


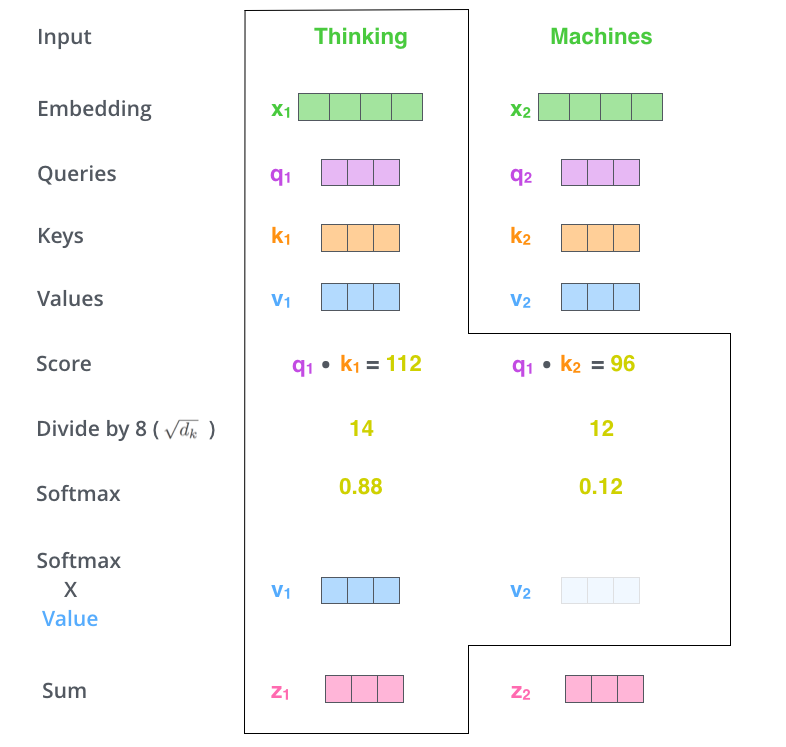
*Visualization of self-attention from Jay Alammar's blog*

The attention is computed as:

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$$

Where:
- $Q$: Query matrix
- $K$: Key matrix
- $V$: Value matrix
- $d_k$: Dimension of keys

## 5. Multi-Head Attention

Instead of performing a single attention function, transformers use multiple attention "heads":

$$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, ..., \text{head}_h)W^O$$

Where each head is:

$$\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$$

## 6. Positional Encoding

Since transformers don't have recurrence or convolution, they need positional information:

For even dimensions (2i):
$$PE_{(pos,2i)} = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)$$

For odd dimensions (2i+1):
$$PE_{(pos,2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)$$

Where:
- $pos$: Position in the sequence
- $i$: Dimension index
- $d_{model}$: Model dimension

## 7. Feed-Forward Network

Each layer contains a position-wise feed-forward network:

$$\text{FFN}(x) = \text{ReLU}(xW_1 + b_1)W_2 + b_2$$

This is applied to each position separately and identically.

In the next part (2/7), we'll dive deeper into the self-attention mechanism and its mathematical foundations.