# LoRA
## Week 1B
----
## 介紹
LoRA 為 Low-Rank Adaptation 的縮寫
在訓練模型時,不對整個模型所有參數都進行訓練
放一個小模型在旁邊,與大模型的輸出合併運算
從而減少反向梯度所需消耗的記憶體使用量
[Paper](https://arxiv.org/abs/2106.09685)
----
## 運作流程
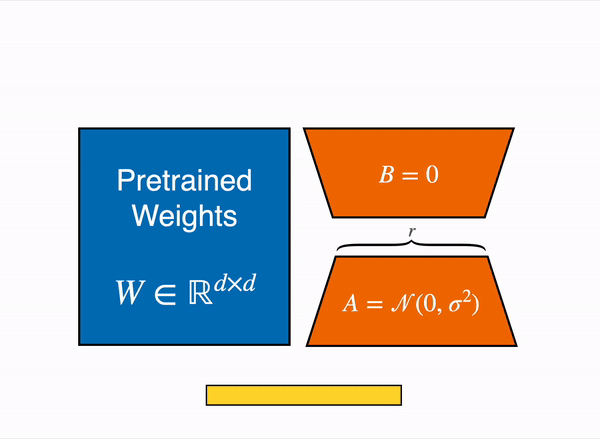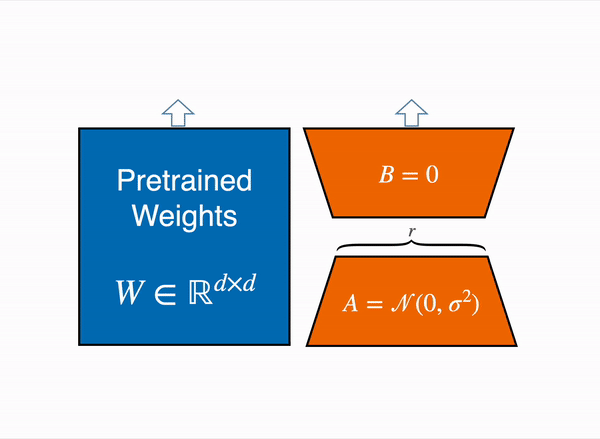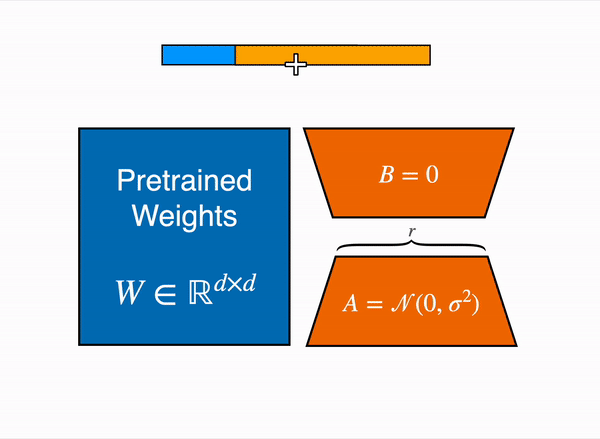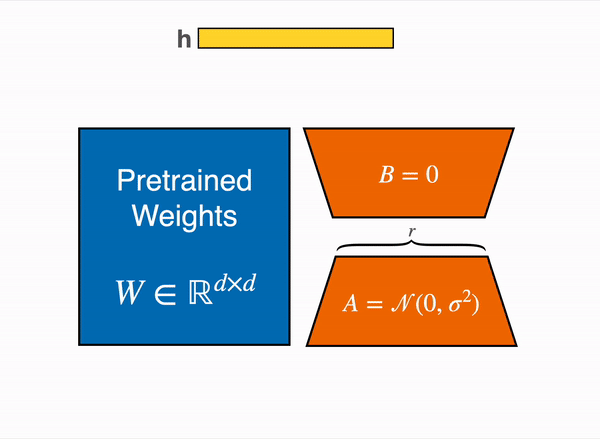
----
## 原始參數量
若 Batch Size 為 $32$
則我們的輸入是一個 $32 \times 100$ 的矩陣 $I$
而模型的權重為 $100 \times 100$ 的矩陣 $W$
最後輸出的結果為 $I \times W$ 為 $32\times 100\times 100$
這樣更新參數量大小為 $100 \times 100=10000$
----
## LoRA 參數量
LoRA 將計算拆解為 $A,B$ 兩個矩陣
分別為 $100\times10$ 跟 $10\times100$ 的矩陣
然後計算 $I\times A\times B$ 得到 $32\times100\times100$
但更新參數量只有 $100\times10+10\times100=2000$
如此一來就減少了八成的參數量
----
## 心生疑問
1. LoRA 為何不會增加參數量呢?
2. 為何矩陣 $W,A,B$ 可以合併呢?
----
## 合併權重
原本的計算為 $I\times W+I\times A\times B$
根據分配律,可以改成 $I\times (W+A\times B)$
$A \in \mathbb{R}^{100 \times 10}\times B\in \mathbb{R}^{10 \times 100}=W' \in \mathbb{R}^{100\times 100}$
$W \in \mathbb{R}^{100\times 100}+W' \in \mathbb{R}^{100\times 100}=W'' \in \mathbb{R}^{100\times 100}$
$W''$ 的大小與原本的 $W$ 一樣
所以參數量並沒有增加,且三個矩陣能夠合併
---
# 實際操作
----
## 安裝套件
+ Parameter-Efficient Fine-Tuning (PEFT)
+ 由 HuggingFace 維護的一個套件,包含 LoRA
```
pip install peft
```
----
## 使用方法
原本的訓練程式碼
```python=
model = ModelCls.from_pretrained("gpt2")
args = TrainingArguments(...)
trainer = Trainer(model, args)
trainer.train()
```
使用 LoRA 的訓練程式碼
```python=
model = ModelCls.from_pretrained("gpt2")
model = get_peft_model(model, LoraConfig(r=8))
args = TrainingArguments(...)
trainer = Trainer(model, args)
trainer.train()
```
[Colab Demo](https://colab.research.google.com/drive/1DAJWDnSdWGxvwuptOpUaqAHK5KRngTv0?hl=en)
---
# 實驗結果
----
## BERT-Tiny
| Comparison | SFT | LoRA | Delta |
|------------|---------:|---------:|-------:|
| Parameters | 4M | 9K | 99.78% |
| GPU Memory | 2560 MiB | 2380 MiB | 7.03% |
| Time Cost | 150s | 120s | 20.00% |
----
## BERT-Base
| Comparison | SFT | LoRA | Delta |
|------------|-------:|-------:|-------:|
| Parameters | 109M | 300K | 99.72% |
| GPU Memory | 22 GiB | 19 GiB | 13.64% |
| Time Cost | ~45m | ~37m | 17.78% |
----
## Performance
| Epoch | SFT-Loss | SFT-Acc | LoRA-Loss | LoRA-Acc |
|:-----:|---------:|--------:|----------:|---------:|
| 1.0 | 0.3401 | 0.8574 | 0.4117 | 0.8134 |
| 2.0 | 0.3080 | 0.8707 | 0.3968 | 0.8174 |
| 3.0 | 0.3050 | 0.8762 | 0.3538 | 0.8442 |
| 4.0 | 0.3056 | 0.8790 | 0.3457 | 0.8492 |
| 5.0 | 0.3084 | 0.8776 | 0.3392 | 0.8523 |
---
# Other
----
## VSCode Server Install Path
+ 因為訓練機的 Home 目錄所在硬碟被塞爆了
+ 所以需要幫 `.vscode-server` 換個位置
+ 可以根據機器設置絕對路徑:
```
"remote.SSH.serverInstallPath": {
"trainer57": "/mnt/ssd4t/.vscode-server",
"trainer32": "/mnt/ssd2t/.vscode-server"
}
```
[Reference](https://github.com/microsoft/vscode-remote-release/issues/472#issuecomment-975745519)
----
## iThome 鐵人賽報名中
由 iThome 舉辦的鐵人賽
連續 30 天,每天寫一篇技術文章
完賽就會給你一個獎牌
[九月開賽,即刻報名!](https://ithelp.ithome.com.tw/2023ironman/event)
{"lang":"zh-TW","description":"地獄貓旅行團第 27 週心得分享","title":"Week 1B - LoRA","slideOptions":"{\"transition\":\"slide\"}","contributors":"[{\"id\":\"c7cbb212-2c41-4dfa-8d85-f8e7fa769bf1\",\"add\":3579,\"del\":479}]"}