###### tags: `Notes` `Big-Oh` `algorithm`
# 時間複雜度
## [速查表](https://kknews.cc/zh-tw/tech/l3y4qng.html)
## [初學者學演算法|談什麼是演算法和時間複雜度](https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E8%AB%87%E4%BB%80%E9%BA%BC%E6%98%AF%E6%BC%94%E7%AE%97%E6%B3%95%E5%92%8C%E6%99%82%E9%96%93%E8%A4%87%E9%9B%9C%E5%BA%A6-b1f6908e4b80)
### 演算法
演算法的簡單定義式:輸入 + 演算法 = 輸出

### 時間複雜度
大 O 符號是用來描述一個演算法在輸入 n 個東西時,總執行時間與 n 的關係。


## [初學者學演算法|從時間複雜度認識常見演算法](https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E6%8E%92%E5%BA%8F%E6%B3%95%E5%85%A5%E9%96%80-%E9%81%B8%E6%93%87%E6%8E%92%E5%BA%8F%E8%88%87%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F%E6%B3%95-23d4bc7085ff)
### 常見的六種時間複雜度與演算法
|Big Oh|演算法|
|-|:-:|
|O(1)|陣列讀取|
|O(n)|簡易搜尋|
|O(log n)|二分搜尋|
|O(n²)|選擇排序法<Br>插入排序法|
|O(n logn)|合併排序法|
|O(2^n)|費波那契數列|
### O(1):陣列讀取
時間複雜度為 O(1) 的演算法,代表著不管你輸入多少個東西,程式都會在同一個時間跑完。
在程式設計中,最簡單的例子就是讀取一個陣列中特定索引值的元素。

```python=
Pokemons = ["卡丘","胖丁","尼龜","比獸","呆獸","種子","小剛"]
print(Pokemons[n])
>> "卡丘"
```
### O(n):簡易搜尋
時間複雜度為 O(n) 的演算法,代表著執行步驟會跟著輸入 n 等比例的增加。
例如當 n = 8,程式就會在 8 個步驟完成。最簡單的例子,就是所謂的簡易搜尋。
```python=
Pokemons = ["卡丘","胖丁","尼龜","比獸","呆獸","種子","小剛"]
for Pokemon in Pokemons:
if Pokemon == "呆獸":
print("找到呆獸!")
break
else:
print("這個櫃子裡不是呆獸")
```
### O(log n):二分搜尋法
a.k.a 終極密碼搜尋法

## [初學者學演算法|排序法入門:選擇排序與插入排序法](https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E6%8E%92%E5%BA%8F%E6%B3%95%E5%85%A5%E9%96%80-%E9%81%B8%E6%93%87%E6%8E%92%E5%BA%8F%E8%88%87%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F%E6%B3%95-23d4bc7085ff)
### O(n²):選擇排序法 (Selection Sort)
時間複雜度為 O(n²) 的演算法,代表著執行步驟會跟著輸入 n 成次方比例的增加。最基礎的排序法之一:選擇排序法(Selection Sort) 是 O(n²) 複雜度的代表。
- **找最小值** :point_right: ==n==
從「未排序好的數字」中找到最小值
- **丟到左邊** :point_right:(n+(n-1)+(n-2)+…+1) = ==n * (n+1) / 2==
把最小值丟到「未排序好的數字」的最左邊,把它標示成已排序好
假設有一個 [41, 33, 17, 80, 61, 5, 55] 的陣列,我們用圖的例子來一步一步理解選擇排序是如何進行,在下面的圖中,我們把尚未排序好的數字用紅色標示,這輪找到的最小值以橘色標示,排序好的以藍色標示。
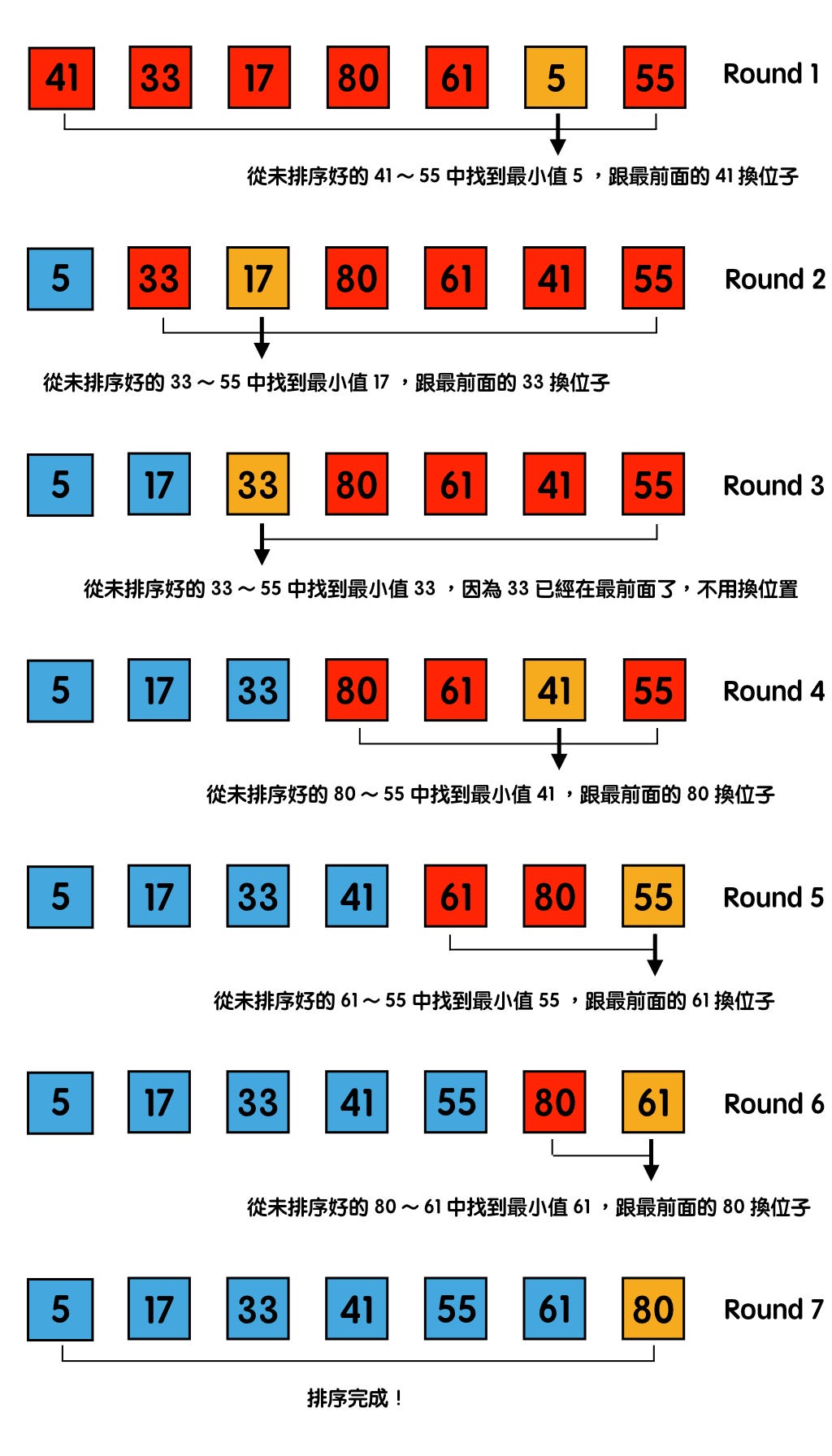
- **結合找到最小值與丟到最左邊**
把上面的兩個結果加起來,(n * (n+1) / 2) + n = n * (n+3) / 2。回想一下我們在這篇提到的,時間複雜度只取最高次方項並省略所有係數,因此雖然選擇排序的步驟數是 n * (n+3) / 2,其時間複雜度我們還是會記為 O(n²)。
### O(n²):插入排序法 (Insertion Sort)
同樣擁有 O(n²) 時間複雜度,插入排序法 Insertion Sort 則是另外一個非常常見的排序法。簡單來說,插入排序法就是你玩撲克牌時用到的排序
- 讀一個數字
從「未排序過的數字」中讀取一個數
- 插入合適位置
把這個讀取的數往前插入一個位置
現在,我們重新使用 [41, 33, 17, 80, 61, 5, 55] 的陣列,在下面的圖中,我們把尚未排序過的數字用紅色標示,這輪要插入的值以橘色標示,排序過的以藍色標示。

- **讀一個數字與結合插入合適位置**
我們在「插入合適位置」需要 1+2+3+…+n 個步驟、在「讀一個數字」需要總共 n 個步驟,計算後 就會得到和選擇排序法相同的 n * (n+3) / 2 個步驟,其時間複雜度我們記為 O(n²)。
### O(n logn):合併排序 (Merge Sort)
時間複雜度為 O(n log n) 的演算法,代表著執行時間會隨著以二為底的 log n 再乘上 n 成長。最常見的例子是合併排序法 (Merge Sort) 與快速排序法 (Quick Sort),而本篇文章將以新手比較好掌握的合併排序法為例。

- 每回合的合併要一個一個比對,需要花:O(n)
- 每回合都縮減一半,所以總共需要回合數:O(log n)
- 所以總共是 O(n log n)
## [初學者學演算法|從費氏數列認識何謂遞迴](https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E5%BE%9E%E8%B2%BB%E6%B0%8F%E6%95%B8%E5%88%97%E8%AA%8D%E8%AD%98%E4%BD%95%E8%AC%82%E9%81%9E%E8%BF%B4-dea15d2808a3)
### O(2^n):費波那契數列 (Fibonacci numbers)
時間複雜度為 O(2^n) 的演算法,代表著執行步驟會是 2 的 n 次方。實務上來說,這樣的執行效率非常的慢,例如當輸入為 100 時,執行步驟就會暴增到 30 位數,等於即使每秒都能執行 1 百億個步驟,也需要個天荒地老 1 千億年才能完成。因此,這樣的時間複雜度是大部分工程師在設計演算法時想要避免的。
而這樣的時間複雜度,最常見的例子是以遞迴計算費波那契數列 (Fibonacci numbers)。
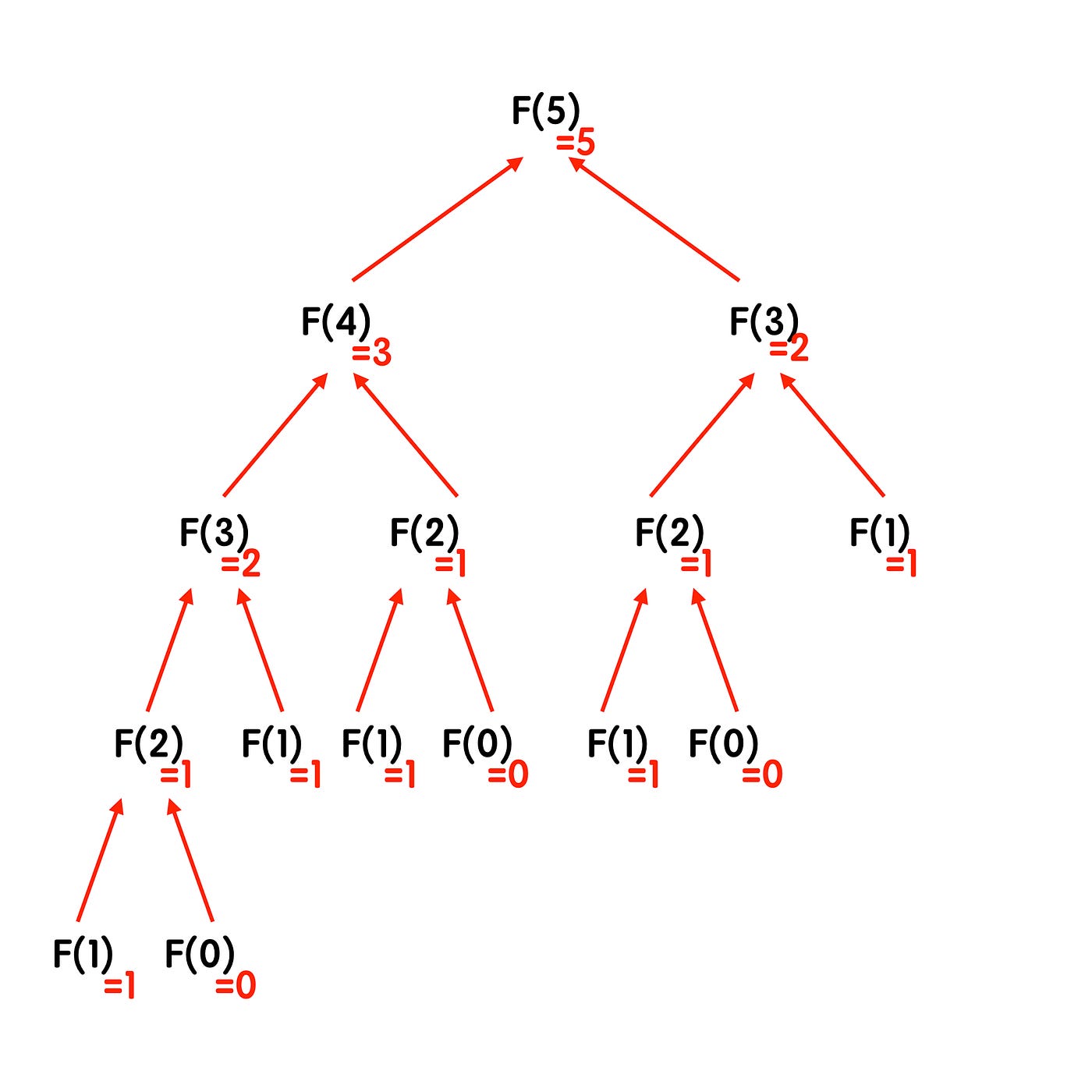
```python
計算費波那契數列第 10 項的程式碼如下:
def fibo(n):
if n == 0:
return 0;
elif n == 1:
return 1;
return fibo(n-1) + fibo(n-2)
print(fibo(10))
```
- 每往下一層,步驟數變 2 倍
- 總共有 n 層
- 時間複雜度:O(2^n)
### 同場加映:如何加速計算費氏數列的演算法
在上面我們提到過,時間複雜度 O(2^n),在實務上非常的慢。因此,我們就要來試著改善上面的演算法,看看能不能讓他加速一點。
我們可以「用空間換取時間」,把每一個算過的值都用一個大表依序記下來。這樣當我們想要知道 F(3) 是多少時,我不用重新計算 F(2)+F(1),只要去大表上找到 F(3) 的答案就好。讓我們以計算 F(10) 為例:
```python
table = [0]*3
table[0] = 0
table[1] = 1
for i in range(2,11):
table[2] = table[1] + table[0]
table[0] = table[1]
table[1] = table[2]
print(table[2])
```
算每一項的同時我們需要去讀取前兩項的值,並把它加起來,總共需要三個步驟。而我們總共需要算 n-1 次,所以總共的步驟數是 3(n-1) 次,只看最高次方項並拔掉係數後,我們就可以得到加速後的時間複雜度:O(n)
## Bubble Sort、Bucket Sort
### O(n²):氣泡排序法 (Bubble Sort)
氣泡排序法(Bubble Sort)是最容易理解和實作的一種排序演算法,也翻譯作冒泡排序法。由於它很容易學習,所以也是許多演算法課程中第一個學習的排序演算法。
- 逐步比較第 n 個位置和第 n+1 個位置元素的大小
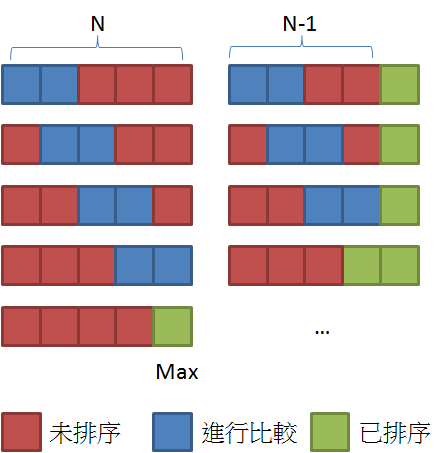
總共需要進行 n 個回合,每個回合進行 n-i 次。故時間複雜度為O(n²)
### O(n²):桶排序法 (Bucket Sort)
桶排序法會將資料先分類丟進不同的桶子中,
接著再將所有桶子內的數列以==插入排序==等適合**少量**資料的演算法進行排序之後,
再依照桶子的順序把桶子中的元素串接在一起,如此一來就能完成所有排序。

- 最差情況:
當所有的元素都在同一個桶中,時間複雜度為桶內的排序演算法速度 O(n²)
- 最優情況:
元素完全分散在 m 個不同的桶子中,完全不需進行排序。O(n + m)
## 附件
### 資料結構

### 排序

## 圖形

## Heap

 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet