HMM POS Tagging

--- tags: NLP title: HMM POS Tagging ---     ## Hidden Markov Models for POS Tagging **Data**: [Train](https://www.dropbox.com/s/x9n6f9o9jl7pno8/train_pos.txt?dl=0), [Test](https://www.dropbox.com/s/v8nccvq7jewcl8s/test_pos.txt?dl=0), [Tag Distribution For Words (optional)](https://www.dropbox.com/s/l18qvx0uqja7ddf/tag_logit_per_word.tsv?dl=0) Let us define the HMM model for assigning POS tags. Let's assume that we observe the words in a sentence. The emission of words is governed by a hidden Markov process that explains the transition between POS tags. 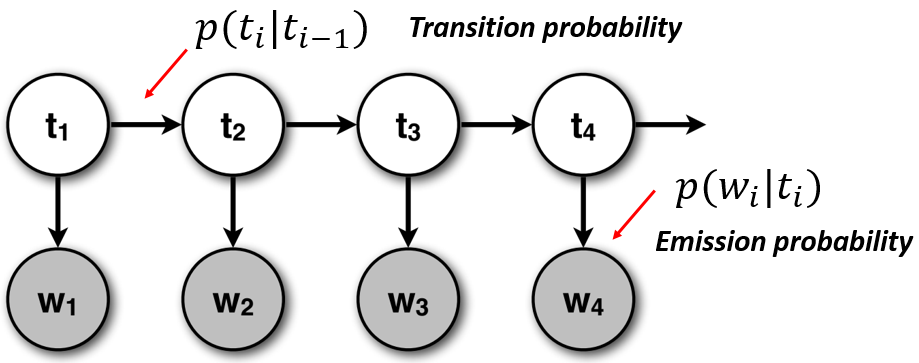This HMM model can be described with the following graph ![](http://www.cs.virginia.edu/~hw5x/Course/TextMining-2019Spring/_site/docs/codes/HMM.PNG) where $t_i$ is a tag at position $i$ and $w_i$ is a word at position $i$. The joint probability of words and tags can be factorized in the following way $$ \begin{aligned} p(w_1,...,w_N,t_1,...,t_N) &= \prod_{i=1}^N p(w_i|t_i)p(t_i|t_{i-1}) \\ &= \prod_{i=1}^N \frac{p(t_i|w_i)p(w_i)}{p(t_i)} p(t_i|t_{i-1}) \\ &= \prod_{k=1}^N p(w_k) \prod_{i=1}^N \frac{p(t_i|w_i)}{p(t_i)} p(t_i|t_{i-1}) \end{aligned} $$ assume $p(t_1|t_0) = p(t_1)$ for the simplicity of notation. We took the probability of each word in the sequence out of the product because, as we will see later, we can ignore them during the optimization. :::warning Do not work with probabilities directly ::: Making your calculations with probabilities directly is bad for two reasons: 1. When multiplying a lot of probabilities, you will face the problem of floating point underflow 2. Multiplication operation is slow. You will have much higher performance if you calculate log of probability and then add log probabilities together $$ \log p(w_1,..,w_N,t_1,..,t_N) = \sum_{k=1}^N \log p(w_k) + \sum_{i=1}^N \left[ \log p(t_i|w_i) - \log p(t_i) + \log p(t_i|t_{i-1}) \right] $$ ## [Viterbi Algorithm](https://web.stanford.edu/~jurafsky/slp3/8.pdf) In the problem of POS tagging, we want to maximize the joint probability of assigning the tags to the input words. Thus, the problem can be solved with a maximization objective $$ \hat{t_1},..,\hat{t_N} = \underset{t_1,..,t_N}{argmax} \left( \sum_{i=1}^N \log p(t_i|w_i) - \log p(t_i) + \log p(t_i|t_{i-1}) \right) $$ The additive term $\sum_{k=1}^N \log p(w_k)$ does not influence the result of summation, and therefore can be omitted. Now, we want to solve this problem optimally, meaning given the same input, and the same probability distributions, you find the best possible answer. This can be done using the Viterbi algorithm. Assume that you have an HMM where the hidden states are $s={s_1, s_2, s_3}$, and the possible values of the observed variable $c={c_1,c_2,c_3,c_4,c_5,c_6,c_7}$. Given the observed sequence $\mathbf{y}=[c_1,c_3,c_4,c_6]$, the Viterbi algorithm tries to estimate the most likely transitions $\mathbf{z}=[z_1,z_2,z_3,z_4], z_i\in c$, and store the path of the best possible sequence at every step. Define $$ \delta_t(j) = \underset{z_1,..,z_{t-1}}{max}{p(\mathbf{z}_{1:t-1}, z_t=j | y_{1:t})} $$ This is the probability of ending up in state $j$ at time $t$, given that we take the most probable path. The key insight is that the most probable path to state $j$ at time $t$ must consist of the most probable path to some other state $i$ at time $t − 1$, followed by a transition from $i$ to $j$. Hence $$ \delta_t(j) = \underset{i}{max}\ \delta_t(i) p(s_j|s_i) p(y_t|s_j) $$ We also keep track of the most likely previous state, for each possible state that we end up in: $$ a_t(j) = \underset{i}{argmax}\ \delta_t(i) p(s_j|s_i) p(y_t|s_j) $$ That is, $a_t(j)$ tells us the most likely previous state on the most probable path to $z_t = s_j$. We initialize by setting $$ \delta_1(j) = \pi_j p(y_1|z_j) $$ where $\pi_j$ is a prior probability of a state. If we do not have this available, we can use the best unbiased guess - uniform distribution. The Viterbi algorithm will create two tables, that will store the following values Probabilities: |State | t=1, $y_1=c_1$ | t=2 $y_2=c_3$ | t=3 $y_3=c_4$ | t=4 $y_4=c_6$ | |----- | ----| ----- | ------ | ------ | |$s_1$ | 0.5 | 0.045 | 0.0 | 0.0 | |$s_2$ | 0.0 | 0.07 | 0.0441 | 0.0 | |$s_3$ | 0.0 | 0.0 | 0.0007 | 0.0022 | Best previous state: |State | t=1, $y_1=c_1$ | t=2 $y_2=c_3$ | t=3 $y_3=c_4$ | t=4 $y_4=c_6$ | |----- | --- | --- | --- | --- | |$s_1$ | - | 1 | 1 | 1 | |$s_2$ | - | 1 | 2 | 2 | |$s_3$ | - | - | 2 | 2 | The solution can be visualized as follows ![](https://i.imgur.com/eLwqw1j.png) *Source: Machine Learning Probabilistic Perspective, Chapter 17.4.4* For more thorough overview of Viterbi algorithm, refer [here](https://web.stanford.edu/~jurafsky/slp3/8.pdf) ## Dataset Description You are going to use a modified conll2000 dataset to train your HMM tagger. The dataset has the following format ``` word1_s1 pos_tag1_s1 word2_s1 pos_tag2_s1 word1_s2 pos_tag1_s2 word2_s2 pos_tag2_s2 word3_s2 pos_tag3_s2 word1_s3 pos_tag1_s3 ... wordK_s3 pos_tagK_s3 ... ... ... wordM_sN pos_tagM_sN ``` Where `s*` corresponds to different sentences. Every line contains an entry for a single word. Sentences are separated from each other by an empty line.   -->  -->  -->     *[POS]: part of speech *[HMM]: Hidden Markov Model *[MLE]: maximum likelihood *[UD]: Universal Dependencies *[TSV]: Tab Separated Value