---
title: 量子コンピュータについて - 量子力学について
tags:
- "量子力学"
- "量子コンピュータ"
---
# 量子コンピューティング
## 1. そもそも量子とは
- 古典力学において、あらゆる物理量は実数の連続値を取る。
- これは例えば、エネルギー、座標、質量、電荷量などの量には最小単位がないと考えられてきたということ。
- 現代的にはこの考えは正確ではなく、実際にはこのような物理量は離散値を取ることが分かっている。
- 例えば、ある周波数の電磁波の持つエネルギーはその周波数における光子1個のエネルギーの整数倍となるし、電荷の量は電気素量、つまり電子の持つ電荷の整数倍となる。
- 要するに「量子」とは、ここでいう光子や電子のような、離散的な物理量の最小単位となりそのキャリアを果たすような粒子のことである。
- ところで、量子は必ずしも物質的なものとは限らない。
- 電子や核子、原子核のような物質を構成する粒子が量子として記述できることもあるし、光子のように力を媒介する素粒子が量子として記述されることもある。さらには、音子(フォノン/phonon)や正孔(ホール/\[electron\] hole)のように何らかの系と場の相互作用が離散的に振る舞い、恰も粒子が存在するかのように捉え、それを量子として記述することもある。
- ここでの「存在する」は日常語のそれである。ある面を捉えれば、フォノンや正孔は確かに存在しているとも言える。
- だが、これらの量子の基本的な性質はすべて共通していて、それは何らかの現象に際して何らかの物理量の最小単位のキャリアやパケットのように働くということ。
## 2. 量子力学の成立
### 2.1. 量子の導入
- 初めて量子という概念に言及したのは、**マックス・プランク**。
- 1900年にエネルギー量子仮説を発表。
- これこそが現代物理学の二本柱の片割れ、量子力学の発端といえそう。
- ざっくりと説明すると、黒体が電磁波を発するときそのエネルギーは離散的な値を取るという仮説。
- 黒体とは: あらゆる波長の電磁波を完全に吸収し、あるいは熱放射するような物体。現実には存在しない。理想気体や完全剛体のような、モデルを簡単に記述するための理想的なもの。
- プランク定数や量子化など、基礎的かつ重要な概念を導入した。
- 量子化(quantize): 古典力学で連続な値を取るような物理変数を、量子条件を満たすような離散値を取るように変形すること。
- 量子条件: 量子化した離散値が物理的に実現可能であるための制約条件。水素原子モデルにおけるボーアの量子条件など。例えば、ボーアの量子条件を破るような電子軌道は安定して存在できず、原子核に吸収されてしまう。
- **アルベルト・アインシュタイン** がエネルギー量子仮説をもとに、光量子仮説を発表
- 当時、光は粒子であるか波動であるかが未解決問題だった。
- 波動説でしか説明できない現象(縞干渉や回折)の存在がトーマス・ヤングによって実験的に報告される(ヤングの実験)
- ヤングの実験は高校物理で多分みんな履修したはず。いわゆる二重スリット実験ってやつ。
- 波動説の弱点は「**エーテル**」なる何かを持ち出さないとうまく説明できなかったこと。当時はどのように光が空間を伝わるのかも未解明。
- 一応1865年に**ジェームズ・C・マクスウェル**が**マクスウェル方程式**を発表しているが……。
- なんなら1888年にハインリヒ・ヘルツによって電磁波の存在が実験的に報告されている。
- 誰よその男: 周波数の単位、ヘルツの由来になったおっさん。そこそこ重要な人。
- 光の性質が明らかになるにつれて、エーテルはどんどん***トンデモ性質***が仮定されるようになった。
- 空間に充満する***流体***であるはず
- 質量も粘性も0
- (超高周波の光を媒介するので)鋼よりも***剛性が高い*** ← !?!?!?!?
- 非圧縮性流体
- (光を通すので)完全に透明かつ極めて稠密
- どう考えても無理がありすぎます、ありがとうございました。
- 一方、粒子説でしか説明できない現象(光電効果や先述の黒体放射)もあった。
- 光電効果は例のおっさん、ハインリヒ・ヘルツによって報告された現象。
- でもこのおっさん自分の発見の重要性を全く理解していなかったらしい。可哀そうが過ぎる。
- 1905年にアインシュタインが光のエネルギーは周波数に応じた最小単位を持ち、それを基本とした離散値を取るという仮説(=光量子仮説)を提唱
- 実は後追いでギルバート・ルイスとかいうおっちゃんが**相対論的効果を完全に無視**した光の粒子説で諸々の現象を説明する非ニュートン力学の公準系を提唱している。
- いくら何でも無理があろうと思われます……が、いくつかの重要なアイデアを提唱
- 光子が運動量を持つこととか、静止していない物体は静止しているときよりも質量が増えることとか
- 1909年にアインシュタインは「粒子説」と「波動説」のエーテルによらない統合を提唱
- 実は1095年に発表した特殊相対性理論でエーテルの存在を完全否定している。そりゃそう。エーテルに要求される性質はどう考えても無理がある。
- 1923年に**アーサー・コンプトン**がコンプトン効果を発見。光量子仮説が正しいことが証明された。
- コンプトン効果: 物体に照射されて散乱したX線の波長が照射したX線の波長よりも長くなる現象。X線が電子と衝突して非弾性散乱(質点の非弾性衝突と同じ現象)を起こすことが確かめられた。
- コンプトン効果の発見によって、光は波長を持った粒子であることが確実になった。
- つまり、光は「粒子であって波でもある」が大正解。
- 結果、粒子であることが明らかになった光量子は光子と呼ばれることに。
- **ルイ・ド・ブロイ**「もしかして光子以外の粒子も波としての性質を持っているのでわ!?!?」
- 1924年に「ド・ブロイ波(物質波)」を発表。物質がその運動量に対応した波長の光として振る舞うことを予言。
- ド・ブロイ波の波長$\lambda$は運動量$p$に反比例する。$h$はプランク定数。
$$\lambda = \frac{h}{p}$$
↑こんな式。
- 1927年にド・ブロイ波が実際に存在することが実験的に確認された。
- ところでこの辺のスピード感ヤバくない?当時インターネットなんてもちろんなかったよ!?
- **ニールス・ボーア**、ラザフォードによる原子モデルが実現可能ではないことを指摘
- ラザフォードが「電子が原子核の周りを回っている」というモデルを提唱したのは1911年。現代的なイメージとも近い、結構イケてるモデル。
- 既存の物理学の知識を当てはめると、電子は原子核の周りを回り続けられない(エネルギーの大部分をすぐに電磁波として放出して失ってしまう)ことが問題。
- 1913年にボーアは定常状態にある電子は電磁波を放出しないことと、電子が定常状態であれる条件(=ボーアの量子条件)を提唱。
- ところで、のちにボーアの量子条件にド・ブロイ波の式を当てはめてみると、電子軌道における電子のド・ブロイ波が電子軌道上に定常波として存在できることが判明
- これすごい面白い。高校の頃に原子物理の授業で聞いたとき、すごく感動した思い出がある。
- 1920年、**アルノルト・ゾンマーフェルト**が異常ゼーマン効果を説明するために**g因子**を導入
- g因子は2という整数値の無次元量を取ることを示した。
- 異常ゼーマン効果: 磁場の外にあるときの原子の電磁波スペクトルが、磁場の中において複数のバンドに分裂して観測される現象。
- これは画像見た方が早い。画像上の2本線が磁場を掛けていない状態のスペクトルで、画像下の8本線が磁場を掛けた状態のスペクトル。
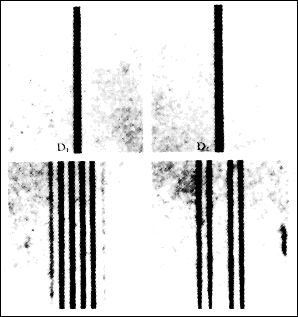
[Wikimedia Commons](https://commons.wikimedia.org/wiki/File:ZeemanEffect.GIF)から引用。
- 1924年、**ヴォルフガング・パウリ**はg因子は非古典的な電子の特性が2値を取ることを示しているとする主張を発表。
- パウリはめちゃくちゃ重要な人。
- 原子核に束縛された電子には、ボーア条件において電子殻を特徴づける整数値$n$と、電子殻内の軌道を特徴づける整数値$l$および$m$で構成される量子状態があり、同一の量子状態を取れる電子は2つまでであるという原理(パウリの排他原理)を提唱した。
- $n$は電子殻を決めるので、「主量子数」なんて言ったりする。
- $l$を同様に方位量子数と言い、$0 \leq l < n$ であるような整数値を取る。
- $m$を磁気量子数と言い、$-l \leq m \leq l$ であるような整数値を取る。
- ここから、1つの電子殻に収まる電子の数がなぜ $2n^2$ なのかも説明できた。
- その後、電子に自転があるとすると理論では説明できなかった角運動量が説明できるという仮説が提唱された。
- しかし、パウリによってスピンは物理的な回転ではありえないことが指摘された。不足する角運動量を補えるような自転速度は光速度を超えてしまう。
- ただし、物理的に回っているわけではないにしろ、角運動量を補っている何かが存在することは確実。結局、スピンという呼び名は残ることになった。
- さらにそののち、電子のスピンの方向が2値をとることが判明。これこそが2自由度の正体だったわけ。
- 上向きと下向きでそれぞれ「↑」「↓」って書き表したりする。
- 各軌道は主量子数と軌道名を合わせて $1s, 2p, 3s, 4f$のように書く。
- 余談だが、軌道の名前の由来は以下の通り:
- $s$軌道: **s**harp から
- $p$軌道: **p**rincipal から
- $d$軌道: **d**iffuse から
- $f$軌道: **f**undamental から
- $g$軌道以降: $f$の次の$g$からはアルファベット順。
- 高校化学でもちょっと触れる: フントの規則
- フントの規則: 電子の軌道配置についてのルール。 $1s \rightarrow 2s \rightarrow 2p \rightarrow 3s \rightarrow 3p \rightarrow 4s \rightarrow 3d \rightarrow\cdots$ という順番で電子が軌道に埋まっていくことを説明する。
### 2.2. 波動関数と量子力学の定式化
- 1920年代後半に入ると、量子状態と運動量のような力学的な値を関連付ける方法論が確立。**行列力学**として定式化される。
- 一方同時期に、エルヴィン・シュレーディンガーがド・ブロイ波を発展させて、**シュレーディンガー方程式**を発見。**波動関数**という概念を導入し、**波動力学**として定式化。
- ところで、この行列力学と波動力学が数学的に等価な理論の別な表現であることにシュレーディンガーが気づいた。しかし、同時に波動関数が表現する波は実空間上のものではないことが明らかになる。
- 1926年にマックス・ボルンが波動関数の観測確率としての解釈を提唱。ボルンの規則っていうやつで、波動関数が確率を記述する云々はここから。
- アインシュタイン「神はサイコロを振らない」
- ところで、不確定性原理も1927年っていうすごくタイムリーなタイミングで発見されている。
- 不確定性原理と波動関数の確率解釈によって、量子力学はちょっとしたパンドラの箱を開けてしまった。
- 波動関数の収縮と観測問題
- アインシュタインは確率解釈を嫌った → **局所実在論**・**隠れた変数理論**
- 波動関数の「収縮」ってどういう現象だろうか?
- コペンハーゲン解釈: 物理的なバックグラウンドは脇に置いておいて、モデルが計算できればそれでよいとする立場。純粋な道具主義的な立場を含む。
- (エヴェレットの)多世界解釈: 波動関数の収縮は起こらず、波動関数の確率に応じた**測度**を持つ複数の世界に分岐するという解釈。
- 測度という物理的な意味が曖昧な量を持ち込んで説明しているあたりが微妙とされている(が、全体的には決定論的に説明できるなどの便利な性質もある)。
- など、いろんな「解釈」があるが、本質的にどれも反証不可能なので科学としての物理学の範囲からは飛び出してしまう。
### 2.3. CHSH不等式の破れの報告と局所実在論の否定
#### 2.3.1. シュテルン=ゲルラッハの実験
- 1922年に**オットー・シュテルン**と**ヴァルター・ゲルラッハ**が行った実験。
- 銀を加熱して蒸発させ、電気的に加速した銀原子ビームに対して、ビーム軸に対して平行に不均一な磁場をかける実験。
- 「銀原子ビームに対して不均一な磁場を掛ける装置」をこれ以降ではSG装置と呼ぶ。
- 古典力学では銀原子の磁気モーメントには向きと大きさの制限がないので、ビームはビーム軸を中心とした分布として観測できると予想。
- 実際に観測してみると、古典力学的予測に反してビームが上下2つに分かれることがわかった。
- これは磁気モーメントの向きと大きさが2状態のみしかないことを示唆している。
- SG装置をビーム軸を軸として回転させると、SG装置の上方向に対してビームが上下に分かれる。このとき、別れた2つのビームが成す角度は**SG装置の傾きによらず一定**。
- これは古典物理学の感覚ではすごく変。古典的にはビームがどんな別れ方をするかはSG装置の傾きに依存するはず。銀原子が持つ磁気モーメントの軸とSG装置の上下軸のなす角度は変化しているはずなのに、なぜかビームの別れ方は変わらない。
#### 2.3.2. CHSH不等式
- SG装置で分割した銀原子ビームのうち、上に出たもののスピンを上向きスピン、下に出たもののスピンを下向きスピンとし、それぞれに$+1$と$-1$という数値を割り当てる。直交座標系$(x, y, z)$のそれぞれの軸を、次のように定める。
- ビーム軸に並行で、ビームの進行方向を正方向とする軸を$x$軸とする。
- 鉛直軸に並行で、重力加速度の逆の方向を正方向とする軸を$z$軸とする。
- $xz$平面に直交し、$z$軸に対して右を正方向とする軸を$y$軸とする。
- 次に、\**空間的に離れた*銀原子を2つ用意して、それぞれ$A$、$B$と呼ぼう。SG装置の上方向をz軸正方向と一致させて計測した$A$のスピンを$\sigma_{zA}$、SG装置の上方向をy軸正方向と一致させて計測した$A$のスピンを$\sigma_{yA}$とする。このときのそれぞれの計測軸に対して、SG装置をビーム軸に対して45度反時計回りに回転させて計測した$B$のスピンを$\sigma_{z'B}$、$\sigma_{y'B}$とする。このとき、物理量$D$を次のように定めよう。
$$\begin{aligned}
D &= \sigma_{yA}(\sigma_{y'B} - \sigma_{z'B}) + \sigma_{zA}(\sigma_{y'B} + \sigma_{z'B})\\
&= \sigma_{yA}\sigma_{y'B} - \sigma_{yA}\sigma_{z'B} + \sigma_{zA}\sigma_{y'B} + \sigma_{zA}\sigma_{z'B}\\
\end{aligned}$$
この式において、$D$が取りうる値の範囲はどうなるのか?
- \**空間的に離れた*: 相対論的な因果律を課す(光の速度を超えた情報伝達は起きず、相互作用は非同時的に発生する)という意味の慣用表現。
- 隠れた変数理論では、$\sigma_{zA}, \sigma_{yA}, \sigma_{z'B}, \sigma_{y'B}$の4つの値が独立に$-1$か$1$の確定した値を持つ。この前提で計算すると、$D$の取りうる値の範囲として$|D|\leq2$が得られる(実際に計算してみると、どのように値を定めても$\pm2$となることがわかる/それぞれの値は$\pm1$しか取らないことに注意せよ)。
- ところで、$D$が取りうる、数学的に最も広い範囲は$|D|\leq4$である。これは、$\sigma_{yA}\sigma_{y'B}, \sigma_{yA}\sigma_{z'B}, \sigma_{zA}\sigma_{y'B}, \sigma_{zA}\sigma_{z'B}$の4つの値がそれぞれ独立に$\pm1$の値を取れる場合にそのような範囲となる。
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet