**Subtask 1** :

Pada subtask ini, karena grup hanya terdiri dari 1 bebek, maka proses reverse dapat diabaikan. Dengan diabaikannya proses reverse, maka dari array yang diberikan, kita hanya perlu mencari berapa pasangan $i$ dan $j$ yang memenuhi syarat. Bisa menggunakan program untuk mempermudah, tetapi mengerjakan manual dengan paper juga tidak memakan waktu lama. Jawaban untuk subtask ini adalah $59$.

---

**Subtask 2** :

Solusi untuk subtask ini dapat diselesaikan dengan melakukan simulasi proses reverse dengan program. Tetapi dapat juga dikerjakan secara manual. Kita hanya perlu mencari $i$ dan $j$ yang memenuhi syarat selama $Q$ kali perubahan formasi. Jawaban untuk subtask ini adalah : $53, 61, 61, 53$, dan $59$

---

**Subtask 3** :

Jumlah $Q$ untuk subtask ini adalah $1$. Sehingga kita cukup melakukan simulasi pada input array yang diberikan. Kompleksitas untuk algoritma subtask 3 adalah $\text{O}(\text{log} N)$ untuk melakukan proses reverse ($N$ adalah banyak data), kemudian proses reverse diulangi sejumlah kelompok yang ada. Maka proses simulasi ini memiliki kompleksitas $\text{O}(N)$. Kemudian setelah proses pertukaran formasi dilakukan, mencari pasangan $i$ dan $j$ yang valid dapat dilakukan dengan menggunakan brute force. Kompleksitas untuk subtask 3 adalah $\text{O}(N^2)$, karena $N$ maksimal adalah $2^4$, maka algoritma ini dapat melewati batas waktu

---

**Subtask 4** :

Algoritma yang sama dengan subtask 3 dapat digunakan, hanya saja kita perlu mengulangi sebanyak $Q$ kali perulangan. Sehingga kompleksitas untuk subtask 4 ini adalah $\text{O}(N^2 \cdot Q)$

---

**Subtask 5** :

Untuk subtask ini, kita memakai pendekatan yang sedikit berbeda dengan subtask sebelumnya. Ini dikarenakan jumlah $N$ yang dapat mencapai nilai 1 juta, maka kompleksitas $\text{O}(N^2)$ sudah pasti tidak dapat melewati time limit yang diberikan.

Pada subtask ini $Q=1$ dan $q_i=0$ dimana formasi tidak diubah sama sekali. Sehingga untuk menyelesaikan subtask ini, kita hanya perlu mencari $f(A)$ dari barisan yang diberikan. Bagaimana caranya?

Observasi (i) :

Kita definisikan $A_{L..R}$ adalah sub-array dari $A$ yang memiliki jangkauan $L..R$. Kita dapat membagi jangkauan untuk setiap $A_{L..R}$ menjadi dua buah sub-array $A_{L..(L+R)/2}$ dan $A_{(L+R)/2 + 1 .. R}$.

Untuk sub array berukuran 1 tidak dapat dibelah menjadi dua bagian lagi. Maka kita dapat melakukan pendekatan divide and conquer untuk membagi sub array menjadi dua sub array yang lebih kecil. Jika digambar, cara memotong sub array menjadi dua bagian ini dapat membentuk sebuah pohon biner seperti dibawah ini :


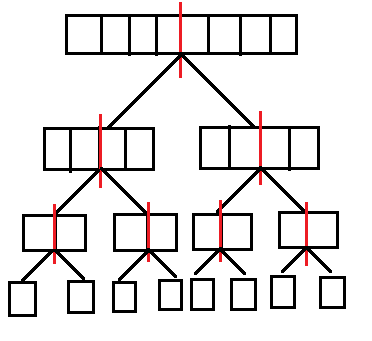
Di setiap sub-array $A_{L..R}$ yang ada pada gambar tersebut dari paling atas hingga paling bawah, kita dapat mengetahui nilai $f(A_{L..R})$. Bagaimana caranya? Kita dapat mencarinya menggunakan binary search.

Mari kita lihat cara mencari nilai $f(A_{L..R})$. Pertama kita urutkan setiap elemen yang berada di subtree bagian kiri, kemudian kita mengurutkan setiap elemen yang berada di subtree bagian kanan.

Untuk setiap elemen $x_l$ di subtree kiri, kita cari ada berapa banyak elemen yang bernilai lebih besar dari $x_l$ di subtree kanan. Kita cari angka terbesar di subtree kanan ($x_r$) yang bernilai lebih kecil dari $x_l$ dan mari kita sebut posisi xr ini adalah lower bound . Karena array di subtree bagian kanan sudah terurut, maka untuk semua nilai yang memiliki posisi di sebelah kiri dari lower bound, sudah pasti seluruh nilai ini lebih kecil dari $x_l$ (monotonik).

Kompleksitas untuk algoritma ini adalah : $\text{O}(N \cdot log^2 N)$ dimana $\text{O}(\text{log} N)$ untuk menjalankan divide and conquer. Di dalam divide and conquer, kita melakukan binary search pada setiap elemen pada subtree kiri. Kompleksitas untuk melakukan binary search pada setiap elemen adalah $\text{O}(N \cdot \text{log} N)$.

---

**Subtask 6**

Untuk menyelesaikan subtask ini, kita perlu menyimpan nilai kekuatan formasi setiap barisan di setiap ketinggian. Mari kita lihat kembali pendekatan divide and conquer yang digunakan dalam subtask 5

Observasi (ii):

Mari kita melihat sebuah grup yang terdiri dari $K$ bebek. Kita definisikan reverse power dari barisan $A$ sebagai $g(A)$ dimana $g(A)$ adalah banyaknya pasangan $i$ dan $j$ yang memenuhi syarat $i<j$ dan $x_i<x_j$. Sehingga dapat kita observasi apabila $A'$ adalah sebuah grup bebek berukuran $K$ setelah di reverse, maka $f(A) = g(A')$ atau $g(A) = f(A')$.


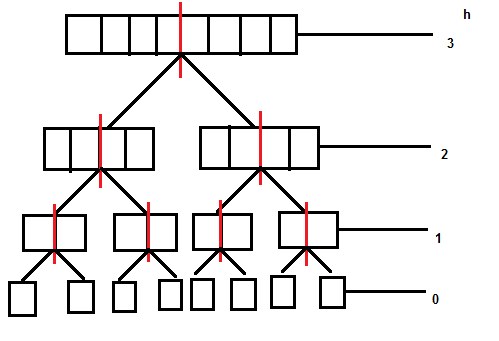
Kita definisikan ketinggian $h$ untuk sub-array $A_{L..R}$ adalah log dari banyaknya elemen pada sub-array tersebut. Untuk setiap ketinggian $h$ dari $0 \ldots \text{log} N$, kita perlu mencatat jumlah dari seluruh nilai $f(A_{L..R})$ dan $g(A_{L..R})$ pada ketinggian tersebut. Mencari nilai $g(A_{L..R})$ dapat dilakukan dengan binary search yang serupa untuk mencari nilai $f(A_{L..R})$ tetapi dengan mencari upper bound pada subtree kanan. Hal ini membuat kita dapat mengetahui banyaknya kekuatan dari sebuah barisan dari sebuah grup dengan ukuran tertentu dalam kompleksitas $O(1)$.

Berdasarkan observasi (ii), kita dapat menyimpulkan bahwa melakukan proses reverse pada seluruh sub-array pada sebuah ketinggian $h$ sama saja kita melakukan penukaran nilai $f(A_{L..R})$ dan $g(A_{L..R})$ untuk semua ketinggian yang lebih kecil dari h. Misalnya kita melakukan reverse pada sub-array yang berada pada ketinggian 2 pada tree di gambar, maka sebetulnya kita tidak perlu mengimplementasikan proses reverse tersebut, kita hanya perlu menukar setiap nilai $f(A_{L..R})$ dan $g(A_{L..R})$ yang berada pada ketinggian lebih rendah daripada $h$.


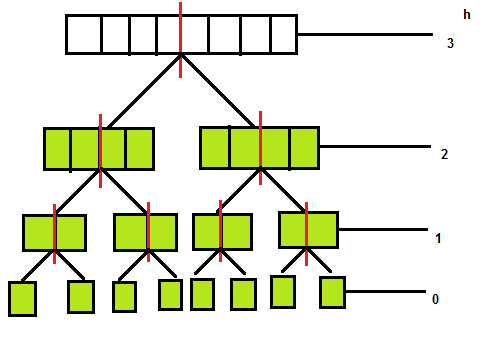
Ilustrasi diatas menggambarkan $h=2$ dan melakukan reverse pada sub-array bagian ini sama saja melakukan penukaran $f(A_{L..R})$ dan $g(A_{L..R})$ yang berada di bawah ketinggian tersebut.

Singkatnya, algoritma untuk menyelesaikan subtask 6 berdasarkan pembahasan diatas adalah sebagai berikut :
- Berdasarkan observasi (ii), melakukan reverse pada sebuah sub-array $A_{L..R}$ di suatu ketinggian $h$ sama saja menukar nilai $f(A_{L..R})$ dan $g(A_{L..R})$ di seluruh ketinggian yang lebih kecil atau sama dengan $h$
- Untuk setiap $h$ dari $0 \ldots q_i$, kita tukar seluruh nilai $f(A)$ dan $g(A)$ yang berada di ketinggian tersebut
- Total dari kekuatan barisan yang baru ini adalah jumlah setiap $f(A)$ dari ketinggian $0, 1, \ldots, log N$

Dengan melakukan algoritma Divide and Conquer yang kita gunakan dalam subtask 5, maka kompleksitas keseluruhan program ini adalah $O(N \cdot log^2 N + Q log N)$. Karena time limit untuk problem ini cukup besar, maka solusi ini dapat menyelesaikan subtask 6

---
Challenge : Bisakah kalian :

- mereduksi kompleksitas algoritma untuk mencari nilai $f(A)$ dan $g(A)$ dari kompleksitas $O(N log^2 N)$ menjadi $O(N log N)$ ?
- menjawab setiap query dalam waktu $O(1)$ ?