Aula Pós - Análise de Componentes Principais
===

###### tags: `posgraduação` `udf` `componentes principais`

https://hackmd.io/s/BkEBMmO_X
e-mail: [e-mail]
---
Update do R, se necessário.

# installing/loading the latest installr package:
install.packages("installr"); library(installr) # install+load installr
 
updateR() # updating R.

---

# O que é?

A Análise de Componentes Principais (PCA) é uma técnica exploratória de dados, que permite visualizar a variação presente em um conjunto de dados com muitas variáveis. É particularmente útil no caso de conjuntos de dados "amplos", em que você tem muitas variáveis para cada amostra, pois é possível reduzir a dimensão do problema.

A PCA procura uma combinação linear de variáveis de tal forma que a variância máxima é extraída das variáveis.

Iremos estudar sobre a aplicação do PCA utilizando o software R.

# Introdução - Matemática

### Vetor Aleatório X com p componentes.

$$
X =
\begin{bmatrix}
x_1 \\
... \\
x_n
\end{bmatrix}
$$

### Vetor de Médias

$$
E[X] =
\begin{bmatrix}
E[x_1]\\
... \\
E[x_n]
\end{bmatrix}
$$

### Matriz de Covariâncias

$$
Cov(X) = \Sigma_{2x2} =
\begin{bmatrix}
\sigma_{11} \ \sigma_{12} \ ... \ \sigma_{1n} \\
\sigma_{21} \ \sigma_{22} \ ... \ \sigma_{2n} \\
... \\
\sigma_{n1} \ \sigma_{n2} \ ... \ \sigma_{nn} \\
\end{bmatrix}
$$

Propriedades da matriz de covariâncias

- simétrica: $\sigma_{ij}$ = $\sigma_{ji}$
- negativa não definida: $a^T$ * $\Sigma$ * $a$ $\geq$ 0
- isso significa que os autovalores da matriz $\Sigma$ são não negativos, isto é, $\lambda_i$ $\geq$ 0.
- a matriz de correlação é semelhante a matriz de covariância, sendo que sua diagonal será 1 e as correlações 2 a 2 dos componentes variando entre -1 e 1.

### Combinação Linear

Seja o vetor a = ($a_1$, ..., $a_p$)' e $X$ um vetor aleatório de tamanho p. Então $Z$ é um combinação linear das variáveis pertencentes ao vetor X.

$Z$ = $a_1$ $X_1$ + $a_2$ $X_2$ + ... + $a_p$ $X_p$

A expectância de $Z$ é dada por:

$E(Z)$ = $a_1$ $\mu_1$ + $a_2$ $\mu_2$ + ... + $a_p$ $\mu_p$

E a variância de $Z$ é dada por:

Var($Z$) = $a'$ $\Sigma_{pxp}$ $a$ = $\sum_{i = j}^{p} a_i^2 \sigma_i^2 + \sum_{i \neq j} a_i a_j \sigma_{ij}$

### Introdução à autovalores e autovetores

Graficamente a idéia básica pode ser vista de uma forma bastante simples. Seja uma imagem formada por um retângulo com 2 vetores segundo (a) da Figura 1. Essa imagem sofre uma ampliação (Transformação) apenas na horizontal, resultando no retângulo (b). Nessa condição, o vetor v2 passou a v2', que não tem a mesma direção do original v2. Portanto, o vetor v2' não pode ser representado por v2 multiplicado por um escalar λ (Número Real). Mas o vetor v1' tem a mesma direção (Reta Suporte) de v1 e, por isso, pode ser representado por v1 multiplicado por um escalar. Diz-se então que v1 é um Autovetor da Transformação e que esse Escalar é um Autovalor associado a v2. Acontece a ampliação de v1 ou mantem-se o tamanho de v1, se o escalar λ ≥ 1; e acontece uma redução de v1 se 0 < λ < 1.


Na definição matemática, consideram-se Transformações Lineares: $T$: $V$ → $V$, onde $V$ é um Espaço Vetorial qualquer.

**Definição**: Um vetor não nulo v, v ∈ **V** é dito um Autovetor de $T$ se existe um número real λ tal que $T$(v)= λ v. O escalar λ é denominado um **Autovalor** de $T$ associado a v. Pode-se concluir que $\vec{v}$ e T($\vec{v}$) tem a mesma Reta Suporte (e assim, mesma Direção). Em outras palavras, o vetor w=T($\vec{v}$) é um múltiplo do vetor $\vec{v}$.

A pergunta central é:

Será que se eu tiver uma transformação linear (ou uma matriz) $T$, existe algum vetor $\vec{v}$ (não-nulo) de forma que $T$ $\vec{v}$ seja um vetor múltiplo de $\vec{v}$ ?

Isto é, será que existe $T$ $\vec{v}$ = $\lambda$ $\vec{v}$, tal que $\lambda$ é um escalar?

Basicamente, estamos procurando a solução da seguinte equação:

$T$ $\vec{v}$ - $\lambda$ $\vec{v}$ = 0
$T$ $\vec{v}$ - $\lambda$ $I$ $\vec{v}$ = 0
($T$ - $\lambda$ $I$)$\vec{v}$ = 0

A solução deste sistema é o núcleo da matriz ($T$ - $\lambda$ $I$) e o espaço-solução desse sistema é chamado de autoespaço.

A solução é dada pelo determinante da matriz, assim:

det($T$ - $\lambda$ $I$) = 0

Assim, é possível achar os autovalores e autovetores.

### Teoria da Decomposição Espectral

**Teorema da decomposição espectral**: Seja $\Sigma_{pxp}$ uma matriz de covariância, então existe uma matriz ortogonal $O_{pxp}$, isto é, $O$ $O´$ = $O´$ $O$ = $I$, tal que:

$$
O´ \Sigma O = \Lambda =
\begin{bmatrix}
\lambda_1 \ 0 \ ... \ 0 \\
0 \ \lambda_2 \ ... \ 0 \\
. \ . \ ... \ . \\
0 \ 0 \ ... \ \lambda_n \\
\end{bmatrix}
$$

Tal que:

- $\lambda_1$ $\geq$ $\lambda_2$ $\geq$ ... $\geq$ $\lambda_n$: são autovalores ordenados em ordem crescente da matriz $\Sigma_{pxp}$
- A matriz $\Sigma_{pxp}$ é similar a matriz $\Lambda_{pxp}$, o que implica dizer:
+ det($\Sigma_{pxp}$) = det($\Lambda_{pxp}$) = $\prod_{i=1}^{n} \lambda_i$;
+ traço($\Sigma_{pxp}$) = traço($\Lambda_{pxp}$) = $\lambda_1$ + ... + $\lambda_p$

Última propriedade importante:

A i-ésima coluna da matriz $O_{pxp}$ é o **autovalor normalizado** $e_i$ correspondente ao autovalor $\lambda_i$, i = 1,2,...,p, que é denotado por:

$$
e_i =
\begin{bmatrix}
e_{i1} \\
e_{i2} \\
... \\
e_{ip}
\end{bmatrix}
$$

Então, a matriz $O$ é dado por $O$ = [$e_{1}$, $e_{2}$,..., $e_{p}$] e pelo teorema da decomposição espectral tem-se:

$\Sigma_{pxp}$ = $O´ \Sigma O$ = $\sum_{i=1}^{p} \lambda_i e_i e_i'$, tal que $e_i'e_j$ = 0, $\forall$ i $\neq$ j.

# Componentes Principais

**Definição 1**: A j-ésima componente principal da matriz $\Sigma_{pxp}$ é definidade como:

$Y_j$ = $e_1$ $X_1$ + $e_2$ $X_2$ + ... + $e_p$ $X_p$

A esperança é dada por:

$E(Y_j)$ = $e_1$ $\mu_1$ + $e_2$ $\mu_2$ + ... + $e_p$ $\mu_p$ = $e_j'$ $\mu_p$

E a variância de $Z$ é dada por:

Var($Z$) = $e_j'$ $\Sigma_{pxp}$ $e_j$ = $\lambda_i$

Ou seja, o autovalor (i) representa a variância de um componente principal (i). Como os autovalores estão em ordenados de forma decrescente, então a primeira componente será a de maior variabilidade e a p-ésima componente a de menor variabilidade.

**Definição 2**: A proporção da variância total de X que é explicada pelo j-ésima componente principal é definda como:

$\frac{Var[Y_j]}{Variância Total}$ = $\frac{\lambda_j}{\sum_{i=1}^{p} \lambda_i}$

**Definição 3**: A proporção total explicada pelas k primeiras componentes principais é definida:

$\frac{\sum{j=1}^{k} Var[Y_j]}{Variância Total}$ = $\frac{{\sum_{j=1}^{k} \lambda_j}}{\sum_{i=1}^{p} \lambda_i}$

# Na prática, o que acontece?


---
:::success
Material de Referência
:::

[Aula de Algebra Linear](https://ocw.mit.edu/courses/mathematics/18-06sc-linear-algebra-fall-2011/least-squares-determinants-and-eigenvalues/eigenvalues-and-eigenvectors/")

[Aula de Equações Diferenciais](https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/ "title")
___

# Dados
Nesta seção, usaremos PCA com conjunto de dados simples e fácil de entender. Você usará o conjunto de dados `mtcars`, conjunto de dados integrante do R. Este conjunto de dados consiste em dados de 32 modelos de carro, retirados de uma revista americana de automóveis (revista 1974 Motor Trend). Para cada carro, você tem 11 recursos, expressos em unidades diferentes (unidades dos EUA), Eles são os seguintes:

* `mpg`: Consumo de combustível (milhas por galão (EUA)): carros mais potentes e mais pesados ​​tendem a consumir mais combustível.

* `cyl`: Número de cilindros: carros mais potentes geralmente têm mais cilindros

* `disp`: Deslocamento: o volume combinado dos cilindros do motor

* `hp`: Potência bruta: esta é uma medida da potência gerada pelo carro

* `drat`: Relação do eixo traseiro: descreve como uma volta do eixo de transmissão corresponde a uma volta das rodas. Valores mais altos diminuirão a eficiência do combustível.

* `peso`: peso (1000 lbs): auto-explicativo!

* `qsec`: tempo de 1/4 de milha: a velocidade e aceleração dos carros

* `vs`: Bloco do motor: isso indica se o motor do veículo tem a forma de um "V" ou se é uma forma reta mais comum.

* `am`: Transmissão: denota se a transmissão do carro é automática (0) ou manual (1).

* `gear`: Número de marchas para frente: carros esportivos tendem a ter mais marchas.

* `carb`: Número de carburadores: associado a motores mais potentes

Observe que as unidades usadas variam e ocupam diferentes escalas.

head(mtcars)

# Retiramos as variáveis "vs" e "am".
mtcars.pca <- prcomp(mtcars[,c(1:7,10,11)], center = TRUE, scale. = TRUE)


#verificar o resultado do PC
summary(mtcars.pca)
#verificar os atributos dos objetos gerados
str(mtcars.pca)

# Plot com os vetores
biplot(mtcars.pca)

As opções `scale` é um indicador lógico dizendo que as variáveis devem estar numa escalar unitária e `center` um valor lógico indicando que a variável deve ser centrada no zero.

---

# Rotações

Por que fazer rotação?

Uma característica importante da análise fatorial é que os eixos dos fatores podem ser rotacionados dentro do espaço variável multidimensional. Como assim?

Suponha que uma pessoa com um alto “status socioeconômico individual” (Fator 1) também vive em uma área que tem um alto “status socioeconômico do bairro” (Fator 2). Isso significa que os fatores devem ser correlacionados.

Consequentemente, os dois eixos dos dois fatores estão provavelmente mais próximos do que uma rotação ortogonal pode torná-los. Aqui está uma exibição da rotação oblíqua dos eixos para nosso novo exemplo:

### Sem rotação


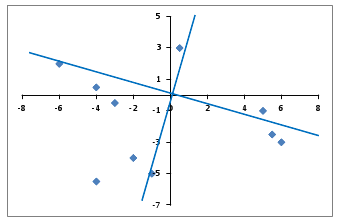
### Com rotação

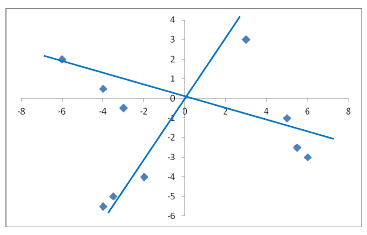
Ou seja, a rotação serve para facilitar a interpretação dos dados.

Programa exemplo:

# Rotação dos componentes
rot.varimax <- varimax(mtcars.pca$rotation)
par(mfrow=c(2,1))
plot(mtcars.pca$rotation[,1],mtcars.pca$rotation[,2])
plot(rot.varimax$rotmat[,1], rot.varimax$rotmat[,2])
dev.off()

## Pergunta:

:::danger
Após a rotação os dados ainda continuam como PCA? :fire:
:::

---
Instalação de Pacotes

install.packages("devtools")
install.packages("ggplot2")
install.packages("dplyr")

library(dplyr)
library(devtools)
library(ggplot2)

install_github("vqv/ggbiplot")
library(ggbiplot)

mtcars.country <- 
c(rep("Japan", 3), 
rep("US",4), 
rep("Europe", 7),
rep("US",3), "Europe",
rep("Japan", 3), 
rep("US",4), 
rep("Europe", 3), "US", 
rep("Europe", 3))

ggbiplot(mtcars.pca,
ellipse=TRUE,
labels=rownames(mtcars),
groups=mtcars.country)


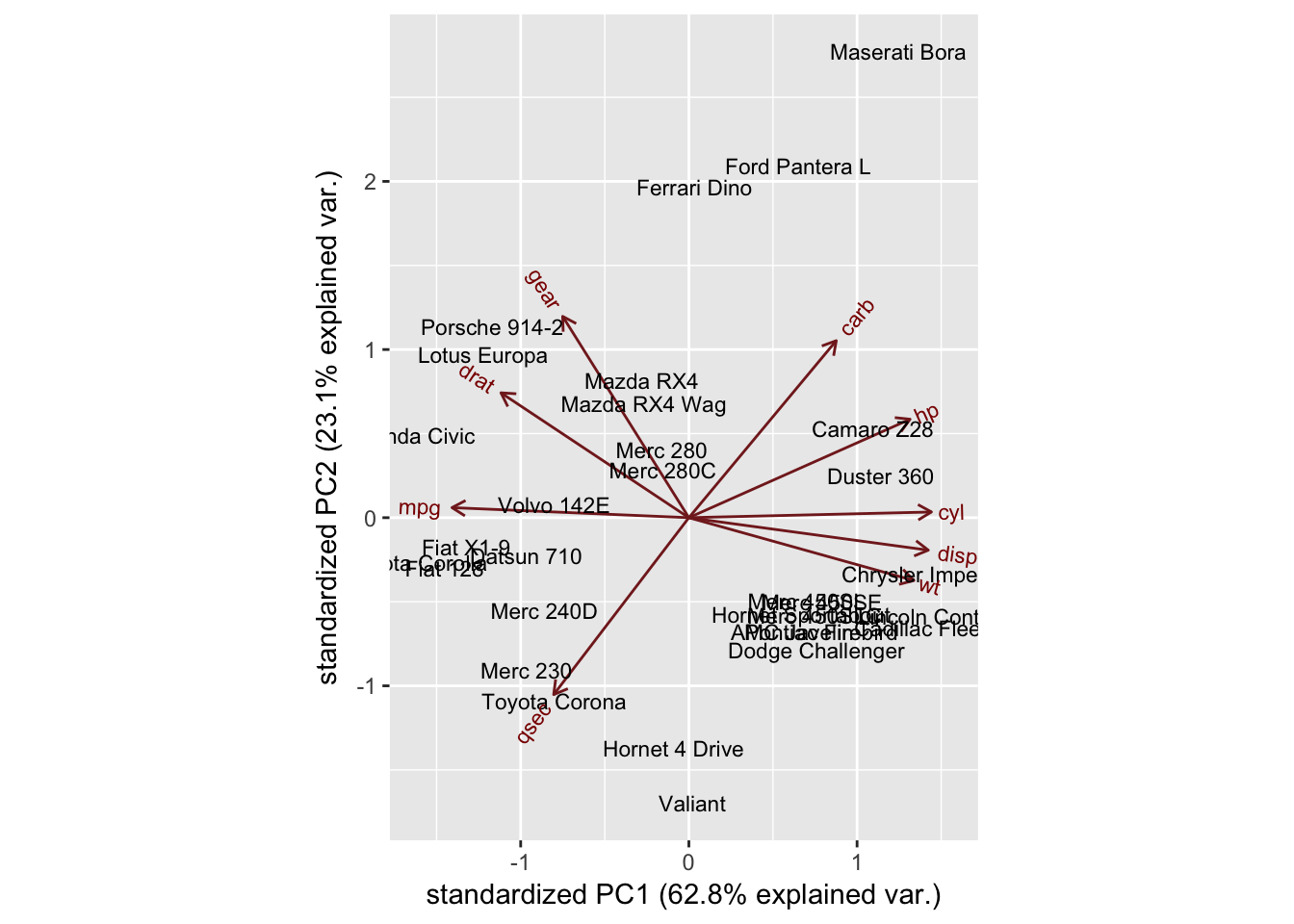
Agora você pode ver quais carros são semelhantes entre si. Por exemplo, o Maserati Bora, o Ferrari Dino e o Ford Pantera L se agrupam no topo. Isso faz sentido, já que todos são carros esportivos. Além disso, observe que eles estão entre os vetores de gear e carb, que indicam maior número de marchas (característica de carros esportivos) e número de carburadores associado a motores mais potentes.

## Intepretando resultados

Talvez se você olhar a origem de cada um dos carros. Você os colocará em uma das três categorias: carros americanos, japoneses e europeus. Você faz uma lista para esta informação, então passa para o argumento de grupos do ggbiplot. Você também definirá o argumento da elipse como TRUE, o qual desenha uma elipse em torno de cada grupo.

### Resultados


Interessante notar que os carros americanos formam um cluster distinto à direita. Olhando para os eixos, você vê que os carros americanos são caracterizados por altos valores para `cyl`, `disp` e `wt`. Carros japoneses, por outro lado, são caracterizados por alto `mpg`. Os carros europeus estão um pouco no meio e menos agrupados do que qualquer um dos grupos.

Você tem muitos componentes principais disponíveis, cada um dos quais mapeiam de maneira diferente das variáveis originais. Você também pode pedir ao ggbiplot para plotar esses outros componentes, usando o argumento choices.

Vamos dar uma olhada no PC3 e PC4.

ggbiplot(mtcars.pca,ellipse=TRUE,choices=c(3,4),   
labels=rownames(mtcars), groups=mtcars.country)


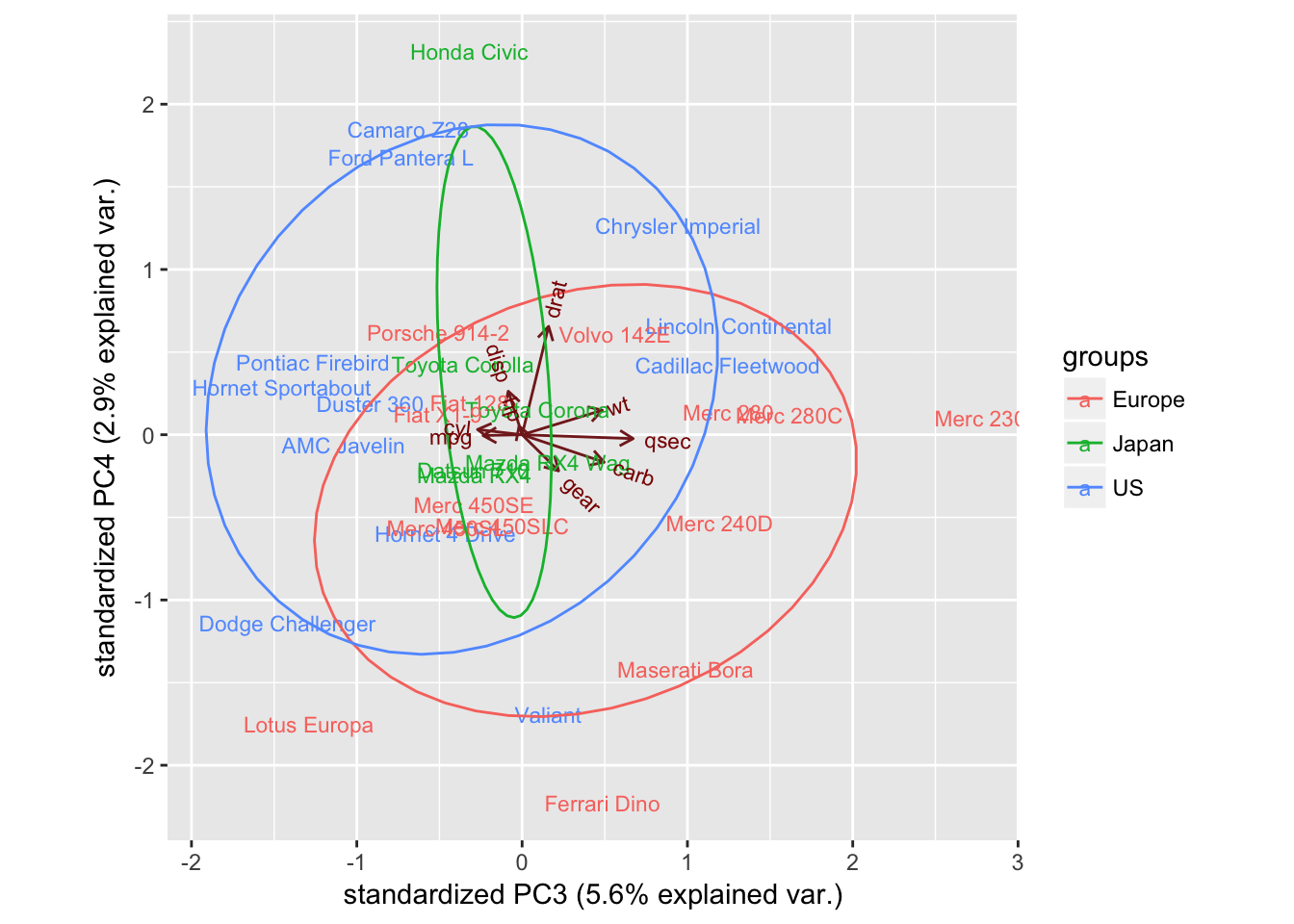
Você não vê muito aqui, mas isso não é muito surpreendente. PC3 e PC4 explicam percentuais muito pequenos da variação total, então seria surpreendente se você descobrisse que eles eram muito informativos e separaram os grupos ou revelaram padrões aparentes.

## Adicionando um novo carro

Digamos que você queira adicionar um novo exemplo ao seu conjunto de dados. Este é um carro muito especial, com estatísticas diferentes de qualquer outro. É super-potente, tem um motor de 60 cilindros, uma incrível economia de combustível, sem engrenagens e é muito leve. Ele é um carro do espaço, chamado `spacecar` vindo diretamente de Júpiter.

Você pode adicioná-lo ao seu conjunto de dados existente e ver onde ele se posiciona em relação aos outros carros?

# Adiconando novas variáveis
spacecar <- c(1000,60,50,500,0,0.5,2.5,0,1,0,0)

mtcarsplus <- rbind(mtcars, spacecar)
mtcars.countryplus <- c(mtcars.country, "Jupiter")

mtcarsplus.pca <- prcomp(mtcarsplus[,c(1:7,10,11)], center = TRUE,scale. = TRUE)

ggbiplot(mtcarsplus.pca, obs.scale = 1, var.scale = 1, ellipse = TRUE, 
  circle = FALSE, var.axes=TRUE, labels=c(rownames(mtcars), "spacecar"), 
  groups=mtcars.countryplus)+
  scale_colour_manual(name="Origin", 
  values= c("forest green", "red3", "violet", "dark blue"))+
  ggtitle("PCA of mtcars dataset, with extra sample added")+
  theme_minimal()+ theme(legend.position = "bottom")


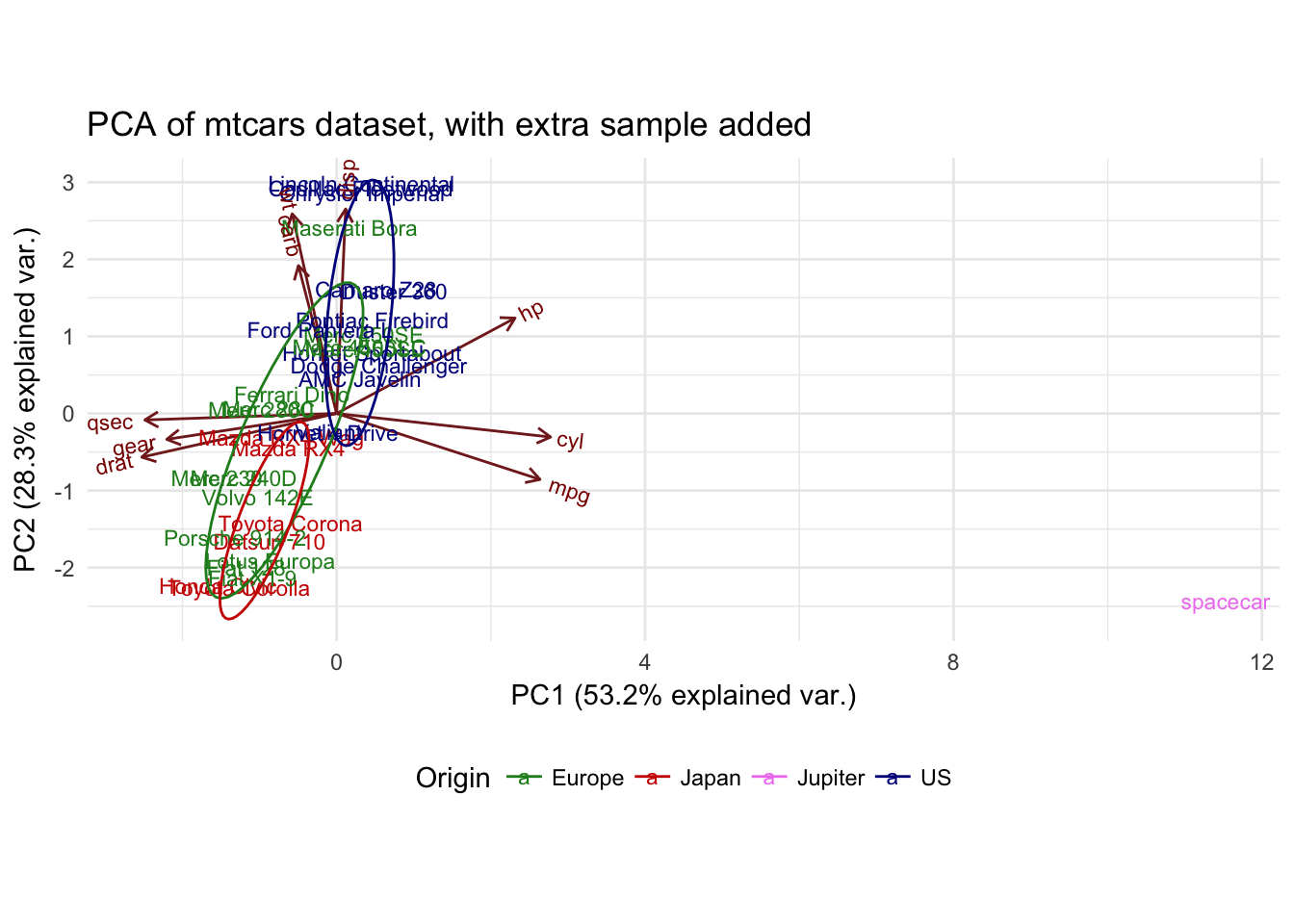
A forma do PCA mudou drasticamente, com a adição desta amostra.

:::warning
Consegue entender por quê? :zap:
:::

Esse resultado ele faz todo o sentido. No conjunto de dados original, você tinha fortes correlações entre determinadas variáveis (por exemplo, cyl e mpg), o que contribuiu para o PC1, separando seus grupos um do outro ao longo desse eixo. No entanto, quando você executa o PCA com a amostra extra, as mesmas correlações não estão presentes, o que distorce todo o conjunto de dados. Nesse caso, o efeito é particularmente forte porque sua amostra extra é um extremo discrepante em vários aspectos.

Se você quiser ver como a nova amostra se compara aos grupos produzidos pelo PCA inicial, é necessário projetá-lo. Como?

## Projetando dados novos no PCA inicial

O que isto significa é que os componentes principais são definidos sem relação com sua amostra de espaço, então você calcula onde o espaço é colocado em relação às outras amostras aplicando as transformações que seu PCA produziu. Você pode pensar nisso como, em vez de obter a média de todas as amostras e permitir que o espaçamento de espaço distorça essa média, você obtém a média das amostras iniciais e observa o espaçador em relação a isso.

O que isto significa é que você simplesmente dimensiona os valores para o espaço em relação ao centro do PCA (`mtcars.pca$center`). Em seguida, você aplica a rotação da matriz PCA à amostra de espaço. Então você pode usar o `rbind()` os valores projetados para o espaçamento para o resto da matriz `pca$x` e passar isso para ggbiplot como antes:

s.sc <- scale(t(spacecar[c(1:7,10,11)]), center= mtcars.pca$center)
s.pred <- s.sc %*% mtcars.pca$rotation


mtcars.plusproj.pca <- mtcars.pca
mtcars.plusproj.pca$x <- rbind(mtcars.plusproj.pca$x, s.pred)


ggbiplot(mtcars.plusproj.pca, obs.scale = 1, var.scale = 1, ellipse = TRUE, 
  circle = FALSE, var.axes=TRUE, labels=c(rownames(mtcars), "spacecar"), 
  groups=mtcars.countryplus)+
  scale_colour_manual(name="Origin", 
  values= c("forest green", "red3", "violet", "dark blue"))+
  ggtitle("PCA of mtcars dataset, with extra sample projected")+
  theme_minimal()+ theme(legend.position = "bottom")


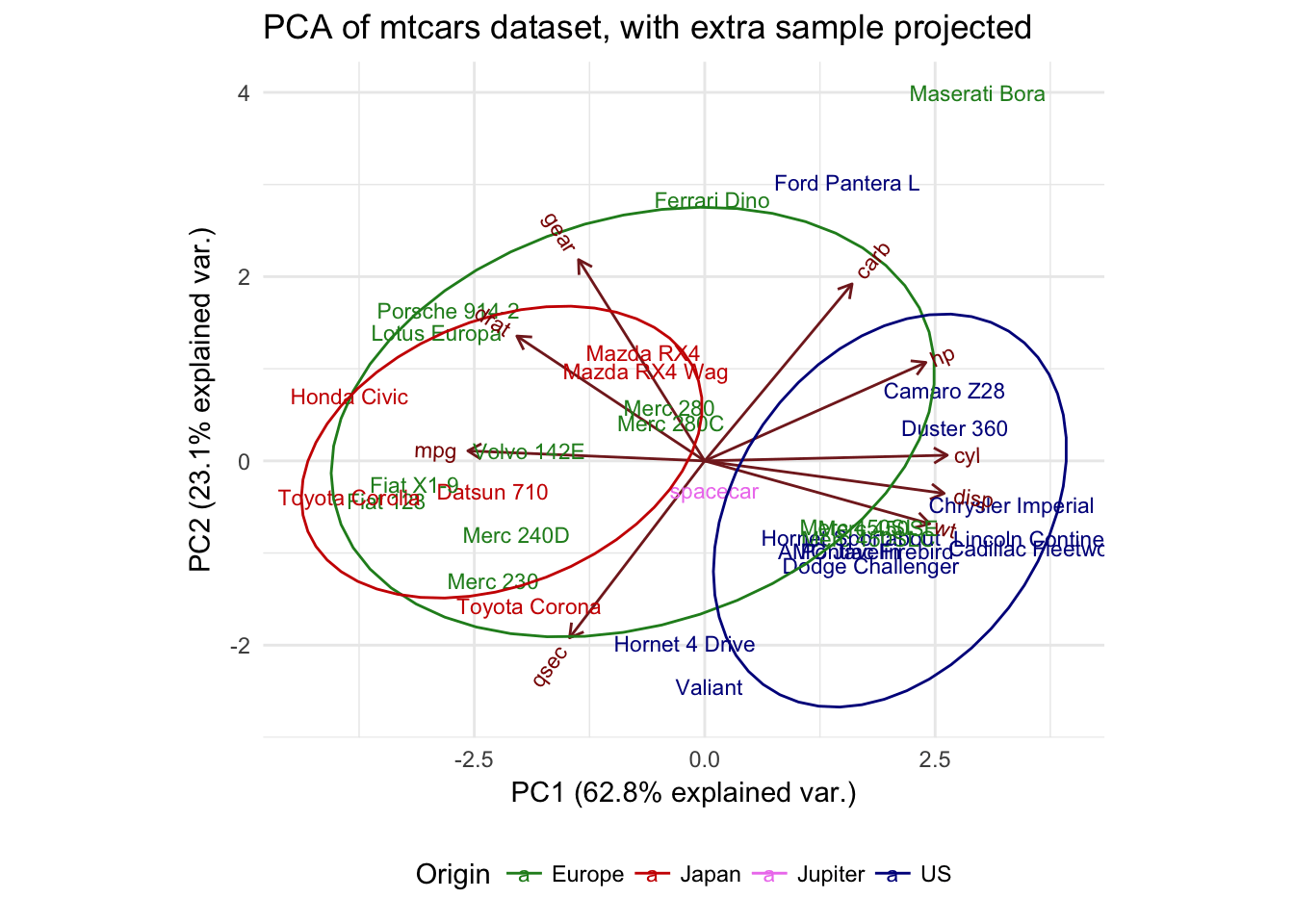
Este resultado é drasticamente diferente. Note que todas as outras amostras estão de volta em suas posições iniciais, enquanto o espaço é colocado perto do meio. Sua amostra extra não está mais distorcendo a distribuição geral, mas não pode ser atribuída a um grupo específico.

Mas qual é melhor, a projeção ou a recomputação do PCA?

Depende um pouco da questão que você está tentando responder.

A recomputação mostra que o espaçamento é um outlier, a projeção diz que você não pode colocá-lo em um dos grupos existentes. A realização de ambas as abordagens é geralmente útil quando se faz uma análise exploratória de dados pelo PCA. Esse tipo de análise exploratória costuma ser um bom ponto de partida antes de você mergulhar mais profundamente em um conjunto de dados. Seus PCAs informam quais variáveis separam os carros americanos dos outros e que o espaçamento é um valor discrepante em nosso conjunto de dados. Um possível próximo passo seria ver se essas relações são verdadeiras para outros carros ou para ver como os carros se agrupam por marca ou por tipo (carros esportivos, 4WDs, etc).

# Avaliação

<i class="fa fa-edit fa-fw"></i> Avaliar os estados americanos segundo 4 variáveis: assassinato, assaultos, população e taxa de estupro.

Avaliação será composta por:

* Programa no R com a resolução (anexo do relatório);
* Relatório com a Interpretação (com conclusão) e gráficos gerados;

Os dados para gerar o relatório será:

data("USArrests")
dado.exerc <- USArrests
head(USArrests,10)

> head(USArrests,10)
            Murder Assault UrbanPop Rape
Alabama       13.2     236       58 21.2
Alaska        10.0     263       48 44.5
Arizona        8.1     294       80 31.0
Arkansas       8.8     190       50 19.5
California     9.0     276       91 40.6
Colorado       7.9     204       78 38.7
Connecticut    3.3     110       77 11.1
Delaware       5.9     238       72 15.8
Florida       15.4     335       80 31.9
Georgia       17.4     211       60 25.8

**Data limite para entrega: 17 Setembro de 2018.**

___



___

Referência:

head(mtcars)

# Retiramos as variáveis "vs" e "am".
mtcars.pca <- prcomp(mtcars[,c(1:7,10,11)], center = TRUE, scale. = TRUE)
#scale = a logical value indicating whether the variables should be scaled to have unit variance before the analysis takes place.
#center = a logical value indicating whether the variables should be shifted to be zero centered.

#verificar o resultado do PC
summary(mtcars.pca)
#verificar os atributos dos objetos gerados
str(mtcars.pca)

names(mtcars.pca)

#Aplicação de uma rotação simples
mtcars.pca$rotation
biplot(mtcars.pca)
ggbiplot(mtcars.pca)
ggbiplot(mtcars.pca, labels=rownames(mtcars))

# Rotação dos componentes
rot.varimax <- varimax(mtcars.pca$rotation)
par(mfrow=c(2,1))
plot(mtcars.pca$rotation[,1],mtcars.pca$rotation[,2])
plot(rot.varimax$rotmat[,1], rot.varimax$rotmat[,2])
dev.off()

Instalação de Pacotes

install.packages("devtools")
install.packages("ggplot2")
install.packages("dplyr")

library(dplyr)
library(devtools)
library(ggplot2)

install_github("vqv/ggbiplot")
library(ggbiplot)


# Intepretando resutlados
mtcars.country <- c(rep("Japan", 3), rep("US",4), rep("Europe", 7),rep("US",3), "Europe", rep("Japan", 3), rep("US",4), rep("Europe", 3), "US", rep("Europe", 3))
ggbiplot(mtcars.pca,ellipse=TRUE,  labels=rownames(mtcars), groups=mtcars.country)

# Adiconando novas variáveis
spacecar <- c(1000,60,50,500,0,0.5,2.5,0,1,0,0)

mtcarsplus <- rbind(mtcars, spacecar)
mtcars.countryplus <- c(mtcars.country, "Jupiter")

mtcarsplus.pca <- prcomp(mtcarsplus[,c(1:7,10,11)], center = TRUE,scale. = TRUE)

ggbiplot(mtcarsplus.pca, obs.scale = 1, var.scale = 1, ellipse = TRUE, circle = FALSE, var.axes=TRUE, labels=c(rownames(mtcars), "spacecar"), groups=mtcars.countryplus)+
  scale_colour_manual(name="Origin", values= c("forest green", "red3", "violet", "dark blue"))+
  ggtitle("PCA of mtcars dataset, with extra sample added")+
  theme_minimal()+
  theme(legend.position = "bottom")

# Nova variável em cima do PCA anterior

s.sc <- scale(t(spacecar[c(1:7,10,11)]), center= mtcars.pca$center)
s.pred <- s.sc %*% mtcars.pca$rotation


mtcars.plusproj.pca <- mtcars.pca
mtcars.plusproj.pca$x <- rbind(mtcars.plusproj.pca$x, s.pred)


ggbiplot(mtcars.plusproj.pca, obs.scale = 1, var.scale = 1, ellipse = TRUE, 
  circle = FALSE, var.axes=TRUE, labels=c(rownames(mtcars), "spacecar"), groups=mtcars.countryplus)+
  scale_colour_manual(name="Origin", values= c("forest green", "red3", "violet", "dark blue"))+
  ggtitle("PCA of mtcars dataset, with extra sample projected")+
  theme_minimal()+
  theme(legend.position = "bottom")



# Avaliação
data("USArrests")
dado.exerc <- USArrests
head(USArrests,10)